Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-16T14:42:15.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Solutal-convection regimes in a two-dimensional porous medium

Published online by Cambridge University Press:  17 February 2014

Anja C. Slim
Anja C. Slim*
Affiliation:
Schlumberger–Doll Research, 1 Hampshire Street, Cambridge, MA 02139, USA
*
†Email address for correspondence: anja.slim@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We numerically characterize the temporal regimes for solutal convection from almost first contact to high dissolved solute concentration in a two-dimensional ideal porous layer for Rayleigh numbers 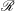$\mathcal{R}$ between 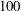$100$ and 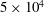$5\times 10^4$. The lower boundary is impenetrable. The upper boundary is saturated with dissolved solute and either impermeable or partially permeable to fluid flow. In the impermeable case, initially there is pure diffusion of solute away from the upper boundary, followed by the birth and growth of convective fingers. Eventually fingers interact and merge, generating complex downwelling plumes. Once the inter-plume spacing is sufficient, small protoplumes reinitiate on the boundary layer and are swept into the primary plumes. The flow is now in a universal regime characterized by a constant (dimensionless) dissolution flux 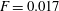$F=0.017$ (the rate at which solute dissolves from the upper boundary). The horizontally averaged concentration profile stretches as a simple self-similar wedge beneath a diffusive horizontal boundary layer. Throughout, the plume width broadens proportionally to 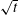$\sqrt{t}$, where $t$ is (dimensionless) time. The above behaviour is parameter independent; the Rayleigh number only controls when transition occurs to a final 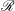$\mathcal{R}$-dependent shut-down regime. For the constant-flux and shut-down regimes, we rigourously derive upscaled equations connecting the horizontally averaged concentration, vertical advective flux and plume widths. These are partially complete; a universal expression for the plume width remains elusive. We complement these governing equations with phenomenological boundary conditions based on a marginally stable diffusive boundary layer at the top and zero advective flux at the bottom. Making appropriate approximations in each regime, we find good agreement between predictions from this model and simulated results for both solutal and thermal convection. In the partially permeable upper boundary case, fluid from the convecting layer can penetrate an overlying separate-phase-solute bearing layer where it immediately saturates. The regime diagram remains almost the same as for the impermeable case, but the dissolution flux is significantly augmented. Our work is motivated by dissolution of carbon dioxide relevant to geological storage, and we conclude with a simple flux parameterization for inclusion in gravity current models and suggest that the upscaled equations could lay the foundation for accurate inclusion of dissolution in reservoir simulators.

JFM classification

Convection: Convection Convection: Convection in porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , pp. 461 - 491
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Backhaus, S., Turitsyn, K. & Ecke, R. E. 2011 Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 106 (10), 104501.CrossRefGoogle Scholar
Barenblatt, G. I. 1996 Scaling, Self-similarity and Intermediate Asymptotics. Cambridge University Press.Google Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Springer.Google Scholar
Busse, F. H. & Joseph, D. D. 1972 Bounds for heat transport in a porous layer. J. Fluid Mech. 54, 521–543.Google Scholar
Canuto, C., Hussaini, M. Y. & Quarteroni, A. 2007 Spectral Methods: Fundamentals in Single Domains. Springer.Google Scholar
Carpenter, M. H., Gottlieb, D. & Abarbanel, S. 1993 The stability of numerical boundary treatments for compact high-order finite-difference schemes. J. Comput. Phys. 108, 272–295.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Cheng, P., Bestehorn, M. & Firoozabadi, A. 2012 Effect of permeability anisotropy on buoyancy-driven flow for $\text {CO}_2$ sequestration in saline aquifers. Water Resour. Res. 48 (9), W09539.Google Scholar
Doering, C. R. & Constantin, P. 1998 Bounds for heat transport in a porous layer. J. Fluid Mech. 376, 263–296.Google Scholar
Elder, J. W. 1968 The unstable thermal interface. J. Fluid Mech. 32 (1), 69–96.Google Scholar
Elenius, M. T. & Johannsen, K. 2012 On the time scales of nonlinear instability in miscible displacement porous media flow. Comput. Geosci. 16 (4), 901–911.CrossRefGoogle Scholar
Elenius, M. T., Nordbotten, J. M. & Kalisch, H. 2012 Effects of a capillary transition zone on the stability of a diffusive boundary layer. IMA J. Appl. Maths 77 (6), 771–787.Google Scholar
Ennis-King, J. & Paterson, L. 2005 Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. SPE J. 10 (3), 349–356.Google Scholar
Ennis-King, J., Preston, I. & Paterson, L. 2005 Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, 084107.Google Scholar
Fornberg, B. 1988 Generation of finite difference formulas on arbitrarily spaced grids. Math. Comput. 51 (184), 699–706.CrossRefGoogle Scholar
Fowler, A. C. 1997 Mathematical Models in the Applied Sciences. Cambridge University Press.Google Scholar
Gasda, S. E., Nordbotten, J. M. & Celia, M. A. 2011 Vertically averaged approaches for $\text {CO}_2$ migration with solubility trapping. Water Resour. Res. 47 (5), W05528.Google Scholar
Graham, M. D. & Steen, P. H. 1994 Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 272 (1), 67–90.Google Scholar
Hanjalic, K 2002 One-point closure models for buoyancy-driven turbulent flows. Annu. Rev. Fluid Mech. 34 (1), 321–347.Google Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2007 Scaling behaviour of convective mixing, with application to geological storage of $\text {CO}_2$. AIChE J. 53 (5), 1121–1131.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108 (22), 224503.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.Google Scholar
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109 (26), 264503.Google Scholar
Horton, C. W. & Rogers, F. T. 1945 Convection currents in a porous medium. J. Appl. Phys. 16, 367–370.CrossRefGoogle Scholar
Howard, L. N. 1964 Convection at high Rayleigh numbers. In Applied Mechanics, Proceedings of 11th Congress of Applied Mathematics (ed. Görtler, H.), pp. 1109–1115.Google Scholar
Kim, M. C. & Choi, C. K. 2012 Linear stability analysis on the onset of buoyancy-driven convection in liquid-saturated porous medium. Phys. Fluids 24, 044102.Google Scholar
Kneafsey, T. J. & Pruess, K. 2011 Laboratory experiments and numerical simulation studies of convectively enhanced carbon dioxide dissolution. Energy Proc. 4, 5114–5121.Google Scholar
Lapwood, E. R. 1948 Convection of a fluid in a porous medium. Proc. Camb. Phil. Soc. 44, 508–521.Google Scholar
LeVeque, R. J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.Google Scholar
Lindeberg, E. & Bergmo, P. 2003 The long-term fate of $\text {CO}_2$ injected into an aquifer. Greenh. Gas Control Tech. 1, 489–494.Google Scholar
Lindeberg, E. & Wessel-Berg, D. 1997 Vertical convection in an aquifer column under a gas cap of $\text {CO}_2$. Energy Convers. Manage. 38, S229–S234.CrossRefGoogle Scholar
Lindeberg, E. & Wessel-Berg, D. 2011 Upscaling studies of diffusion induced convection in homogeneous and heterogeneous aquifers. Energy Proc. 4, 3927–3934.CrossRefGoogle Scholar
MacMinn, C. W., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2012 Spreading and convective dissolution of carbon dioxide in vertically confined, horizontal aquifers. Water Resour. Res. 48 (11), W11516.Google Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2011 $\text {CO}_2$ migration in saline aquifers. Part 2. Capillary and solubility trapping. J. Fluid Mech. 688, 321–351.Google Scholar
2005 In IPCC Special Report on Carbon Dioxide Capture and Storage (ed. Metz, B., Davidson, O., de Coninck, H. C., Loos, M. & Meyer, L.A.), Cambridge University Press.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.Google Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous Media. Springer.Google Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500 (1), 263–281.Google Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in $\text {CO}_2$ storage in saline aquifers. Adv. Water Resour. 33 (4), 443–455.CrossRefGoogle Scholar
Rapaka, S., Chen, S., Pawar, R. J., Stauffer, P. H. & Zhang, D. 2008 Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 609, 285–303.Google Scholar
Rees, D. A. S., Selim, A. & Ennis-King, J. P. 2008 The instability of unsteady boundary layers in porous media. In Emerging Topics in Heat and Mass Transfer in Porous Media Theory and Application of Transport in Porous Media, vol. 22, pp. 85–110. Springer.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 25, 024101.Google Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22, 124103.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Weir, G. J., White, S. P. & Kissling, W. M. 1996 Reservoir storage and containment of greenhouse gases. Transp. Porous Media 23 (1), 37–60.Google Scholar
Wooding, RA 1969 Growth of fingers at an unstable diffusing interface in a porous medium or Hele-Shaw cell. J. Fluid Mech. 39 (3), 477–495.Google Scholar
Xie, Y., Simmons, C. T. & Werner, A. D. 2011 Speed of free convective fingering in porous media. Water Resour. Res. 47 (11), W11501.Google Scholar

Slim supplementary movie

Evolution of the concentration profile at early times forR=50000 and epsilon=0.01 in a small region of the domain near the upper boundary (the lower boundary does not yet play a role in the dynamics). The diffusive, linear-growth, flux-growth and merging regimes are seen.

Download Slim supplementary movie(Video)
Video 574.6 KB

Slim supplementary movie

Evolution of the concentration profile at early times forR=50000 and epsilon=0.01 in a small region of the domain near the upper boundary (the lower boundary does not yet play a role in the dynamics). The diffusive, linear-growth, flux-growth and merging regimes are seen.

Download Slim supplementary movie(Video)
Video 1.8 MB

Slim supplementary movie

Evolution of the concentration profile through all the regimesfor R=50000 and epsilon=0.01 in the full domain.

Download Slim supplementary movie(Video)
Video 9.1 MB

Slim supplementary movie

Evolution of the concentration profile through all the regimesfor R=50000 and epsilon=0.01 in the full domain.

Download Slim supplementary movie(Video)
Video 12.7 MB