1. Introduction
We consider the Brownian motion of a colloidal rigid particle in a binary fluid mixture lying in the homogeneous phase near the demixing critical point. In some combinations of the mixture and particle material, one of the components is preferentially attracted by the particle surface and the preferred component is remarkably adsorbed near the particle surface because of the near-criticality (Beysens & Leibler Reference Beysens and Leibler1982; Beysens & Estève Reference Beysens and Estève1985). The particle motion deforms the adsorption layer, which affects the force exerted on the particle (Lee Reference Lee1976; Omari, Grabowski & Mukhopadhyay Reference Omari, Grabowski and Mukhopadhyay2009; Okamoto, Fujitani & Komura Reference Okamoto, Fujitani and Komura2013; Fujitani Reference Fujitani2018; Tani & Fujitani Reference Tani and Fujitani2018; Yabunaka & Fujitani Reference Yabunaka and Fujitani2020). In other combinations exhibiting negligible preferential adsorption, the particle motion remains still influenced by the near-criticality because of the critical enhancement of the viscosity (Ohta Reference Ohta1975; Ohta & Kawasaki Reference Ohta and Kawasaki1976). This enhancement can also be influenced by the particle motion, as is pointed out in a recent experimental work (Beysens Reference Beysens2019). We briefly mention its background in some paragraphs below.
Let us first assume there are no particles in an equilibrium near-critical binary fluid mixture. The composition can be represented by the difference between (or the ratio of) the mass densities of the two components. The order parameter, which we can take to be proportional to the deviation of the local composition from the critical one, fluctuates about the equilibrium value on length scales smaller than the correlation length, ![]() $\xi$. Correlated clusters, where the order parameter keeps the same sign on average, range over these scales, and are convected to enhance the interdiffusion of the components on larger length scales (Kawasaki Reference Kawasaki1970; Onuki Reference Onuki2002). Thus,
$\xi$. Correlated clusters, where the order parameter keeps the same sign on average, range over these scales, and are convected to enhance the interdiffusion of the components on larger length scales (Kawasaki Reference Kawasaki1970; Onuki Reference Onuki2002). Thus, ![]() $\xi$ affects how the two-time correlation function of the order-parameter fluctuation decays. Writing
$\xi$ affects how the two-time correlation function of the order-parameter fluctuation decays. Writing ![]() $\varGamma _k$ for the relaxation coefficient of its spatial Fourier transform, with
$\varGamma _k$ for the relaxation coefficient of its spatial Fourier transform, with ![]() $k$ denoting the magnitude of the wavenumber vector, we have
$k$ denoting the magnitude of the wavenumber vector, we have
for small ![]() $k$ with
$k$ with ![]() $k\xi$ being finite. Here,
$k\xi$ being finite. Here, ![]() $z$ denotes the dynamic critical exponent for the order-parameter fluctuation and
$z$ denotes the dynamic critical exponent for the order-parameter fluctuation and ![]() $\varOmega$ represents a scaling function, which approaches a constant multiplied by
$\varOmega$ represents a scaling function, which approaches a constant multiplied by ![]() $(k\xi )^{2-z}$ as
$(k\xi )^{2-z}$ as ![]() $k\xi$ becomes much smaller than unity (Siggia, Hohenberg & Halperin Reference Siggia, Hohenberg and Halperin1976; Hohenberg & Halperin Reference Hohenberg and Halperin1977). This leads to
$k\xi$ becomes much smaller than unity (Siggia, Hohenberg & Halperin Reference Siggia, Hohenberg and Halperin1976; Hohenberg & Halperin Reference Hohenberg and Halperin1977). This leads to ![]() $\varGamma _k\propto k^2$ for sufficiently small
$\varGamma _k\propto k^2$ for sufficiently small ![]() $k$, which is expected for the hydrodynamic mode of a conserved quantity. We write
$k$, which is expected for the hydrodynamic mode of a conserved quantity. We write ![]() $k_{B}$ for the Boltzmann constant and
$k_{B}$ for the Boltzmann constant and ![]() $T$ for the temperature of the mixture. The mode-coupling theory for a three-dimensional mixture gives
$T$ for the temperature of the mixture. The mode-coupling theory for a three-dimensional mixture gives
where ![]() $K$ denotes the Kawasaki function with
$K$ denotes the Kawasaki function with ![]() $K(x)\approx 3{\rm \pi} x^3/8$ for
$K(x)\approx 3{\rm \pi} x^3/8$ for ![]() $x\gg 1$ and
$x\gg 1$ and ![]() $K(x)\approx x^2$ for
$K(x)\approx x^2$ for ![]() $x\ll 1$, and
$x\ll 1$, and ![]() $\tilde {\eta }$ represents the shear viscosity (Kawasaki Reference Kawasaki1970; Onuki Reference Onuki2002). In this theory, the weak critical singularity of the viscosity is neglected, and the dynamic critical exponent is found to be three. This theoretical result turns out to be in good agreement with the experimental results (Swinney & Henry Reference Swinney and Henry1973). In the refined calculation of the dynamic renormalization group, the critical enhancement of
$\tilde {\eta }$ represents the shear viscosity (Kawasaki Reference Kawasaki1970; Onuki Reference Onuki2002). In this theory, the weak critical singularity of the viscosity is neglected, and the dynamic critical exponent is found to be three. This theoretical result turns out to be in good agreement with the experimental results (Swinney & Henry Reference Swinney and Henry1973). In the refined calculation of the dynamic renormalization group, the critical enhancement of ![]() $\tilde {\eta }$ is considered, and the value of
$\tilde {\eta }$ is considered, and the value of ![]() $z$ is found to be slightly larger than three (Folk & Moser Reference Folk and Moser2006).
$z$ is found to be slightly larger than three (Folk & Moser Reference Folk and Moser2006).
The mixture is assumed to be at equilibrium in the preceding paragraph. The critical enhancement of the transport coefficients, i.e. the Onsager coefficient for the interdiffusion and the shear viscosity, can be suppressed when a shear is imposed on the mixture. Influences of a simple shear flow are studied theoretically (Onuki & Kawasaki Reference Onuki and Kawasaki1979; Onuki, Yamazaki & Kawasaki Reference Onuki, Yamazaki and Kawasaki1981) and experimentally (Beysens, Gbadamassi & Boyer Reference Beysens, Gbadamassi and Boyer1979; Beysens & Gbadamassi Reference Beysens and Gbadamassi1980). In an example of this flow, the ![]() $x$ component of the velocity is
$x$ component of the velocity is ![]() $y$ multiplied by the constant shear rate
$y$ multiplied by the constant shear rate ![]() $s\,(>\!0)$, with
$s\,(>\!0)$, with ![]() $(x,y)$ denoting two of the three-dimensional Cartesian coordinates. A correlated cluster of the order-parameter fluctuation would be deformed by the shear when its lifetime is longer than a typical time scale of the shear,
$(x,y)$ denoting two of the three-dimensional Cartesian coordinates. A correlated cluster of the order-parameter fluctuation would be deformed by the shear when its lifetime is longer than a typical time scale of the shear, ![]() $1/{s}$. The lifetime for a cluster with the size of
$1/{s}$. The lifetime for a cluster with the size of ![]() $1/k$ is evaluated to be
$1/k$ is evaluated to be ![]() $1/\varGamma _k$, while the cluster size ranges up to
$1/\varGamma _k$, while the cluster size ranges up to ![]() $\xi$. Hence, if the shear is strong enough to satisfy
$\xi$. Hence, if the shear is strong enough to satisfy
the enhancement is suppressed. This condition of strong shear is also derived in terms of the renormalization group, as mentioned in appendix A.
A simple shear flow is a kind of linear shear flow, where the velocity ![]() $\boldsymbol {V}$ at a position is proportional to the positional vector, and can be regarded as a linear combination of a stagnation-point flow and a purely rotational flow (Rallison Reference Rallison1984). These linear shear flows are two-dimensional. A pure-extension flow, being a three-dimensional linear shear flow, and a stagnation-point flow are referred to as elongational flows in Onuki & Kawasaki (Reference Onuki and Kawasaki1980a,Reference Onuki and Kawasakic), where the suppression is studied for some linear shear flows. In a linear shear flow, the time derivative of a directed line segment
$\boldsymbol {V}$ at a position is proportional to the positional vector, and can be regarded as a linear combination of a stagnation-point flow and a purely rotational flow (Rallison Reference Rallison1984). These linear shear flows are two-dimensional. A pure-extension flow, being a three-dimensional linear shear flow, and a stagnation-point flow are referred to as elongational flows in Onuki & Kawasaki (Reference Onuki and Kawasaki1980a,Reference Onuki and Kawasakic), where the suppression is studied for some linear shear flows. In a linear shear flow, the time derivative of a directed line segment ![]() $\boldsymbol {X}$ linking two fluid particles is equal to
$\boldsymbol {X}$ linking two fluid particles is equal to ![]() $(\boldsymbol {\nabla } \boldsymbol {V})^\textrm {T}\boldsymbol {\cdot } \boldsymbol {X}$, where the matrix
$(\boldsymbol {\nabla } \boldsymbol {V})^\textrm {T}\boldsymbol {\cdot } \boldsymbol {X}$, where the matrix ![]() $\boldsymbol {\nabla } \boldsymbol {V}$ represents the homogeneous velocity gradient and superscript
$\boldsymbol {\nabla } \boldsymbol {V}$ represents the homogeneous velocity gradient and superscript ![]() $\textrm {T}$ indicates the transposition. Thus, the exponential of the product of
$\textrm {T}$ indicates the transposition. Thus, the exponential of the product of ![]() $(\boldsymbol {\nabla } \boldsymbol {V})^\textrm {T}$ and the time
$(\boldsymbol {\nabla } \boldsymbol {V})^\textrm {T}$ and the time ![]() $t$ determines how
$t$ determines how ![]() $\boldsymbol {X}$ is stretched and shrunk with time. In the elongational flow, the shear rate
$\boldsymbol {X}$ is stretched and shrunk with time. In the elongational flow, the shear rate ![]() $s$ in (1.3) is given by the largest stretching rate, i.e. the largest eigenvalue of
$s$ in (1.3) is given by the largest stretching rate, i.e. the largest eigenvalue of ![]() $\boldsymbol {\nabla } \boldsymbol {V}$; some details are mentioned in the penultimate paragraph of appendix A.
$\boldsymbol {\nabla } \boldsymbol {V}$; some details are mentioned in the penultimate paragraph of appendix A.
The mean square displacement of a Brownian particle becomes proportional to the time interval as it becomes sufficiently long. The self-diffusion coefficient of the particle is defined as the constant of proportionality divided by twice the spatial dimension. In the study mentioned at the end of the first paragraph (Beysens Reference Beysens2019), it is shown that the self-diffusion coefficient of a Brownian particle in a near-critical binary fluid mixture first decreases and then reaches a plateau as ![]() $T$ approaches the critical temperature
$T$ approaches the critical temperature ![]() $T_{c}$ along the critical isochore in the homogeneous phase. The first decrease should reflect the critical enhancement of
$T_{c}$ along the critical isochore in the homogeneous phase. The first decrease should reflect the critical enhancement of ![]() $\tilde {\eta }$, while the plateau can be regarded as representing the suppression of the enhancement due to the shear caused by the particle motion. Using (1.2) and replacing
$\tilde {\eta }$, while the plateau can be regarded as representing the suppression of the enhancement due to the shear caused by the particle motion. Using (1.2) and replacing ![]() $s$ in (1.3) with the average particle speed divided by the particle radius, Beysens (Reference Beysens2019) estimates the temperature range exhibiting the suppression; the estimated range appears consistent with the observed one. In the present study, we calculate the self-diffusion coefficient for direct comparison with the experimental results.
$s$ in (1.3) with the average particle speed divided by the particle radius, Beysens (Reference Beysens2019) estimates the temperature range exhibiting the suppression; the estimated range appears consistent with the observed one. In the present study, we calculate the self-diffusion coefficient for direct comparison with the experimental results.
In the first three subsections of § 2, we calculate the hydrodynamic force exerted on a rigid spherical particle moving translationally in a fluid mixture quiescent far from the particle. Assuming a typical length scale of the flow to be much larger than ![]() $\xi$, we need not consider dynamics of the order-parameter fluctuation, which is significant only on length scales smaller than
$\xi$, we need not consider dynamics of the order-parameter fluctuation, which is significant only on length scales smaller than ![]() $\xi$ (Furukawa et al. Reference Furukawa, Gambassi, Dietrich and Tanaka2013; Okamoto et al. Reference Okamoto, Fujitani and Komura2013). The mixture is assumed to be incompressible, as in the previous studies mentioned above (Folk & Moser Reference Folk and Moser1998; Onuki Reference Onuki2002). This assumption usually works well in a near-critical mixture prepared experimentally (Anisimov et al. Reference Anisimov, Gorodetskii, Klikov and Sengers1995; Onuki Reference Onuki2002; Pérez-Sanchez et al. Reference Pérez-Sanchez, Losada-Pérez, Cerdeiriña, Sengers and Anisimov2010). When the viscosity is homogeneous, the magnitude of the force is proportional to the particle speed. The constant of proportionality (the drag coefficient) is given by Stokes’ law (Stokes Reference Stokes1851) and is linked with the self-diffusion coefficient of its Brownian motion through the Sutherland–Einstein relation (Einstein Reference Einstein1905; Sutherland Reference Sutherland1905), although the Brownian motion is not always translational. This relation can be derived from the Langevin equation for the particle velocity (Bian, Kim & Karniadakis Reference Bian, Kim and Karniadakis2016), and is further founded on the fluctuating hydrodynamics (Bedeaux & Mazur Reference Bedeaux and Mazur1974), even near the critical point (Mazur & van der Zwan Reference Mazur and van der Zwan1978). In our problem, the suppression of the viscosity enhancement is locally determined by the inhomogeneous shear around the particle, and the drag coefficient can depend on the particle speed in its range to be considered in the Brownian motion. Neither Stokes’ law nor the Sutherland–Einstein relation is applicable when the suppression occurs. Assuming the suppression to remain weak even if it is brought about by the local strong shear, we calculate the drag coefficient. In § 2.4, we use a one-dimensional Langevin equation to link the drag coefficient with the self-diffusion coefficient. Our results are shown and discussed in § 3, and summarized in § 4.
$\xi$ (Furukawa et al. Reference Furukawa, Gambassi, Dietrich and Tanaka2013; Okamoto et al. Reference Okamoto, Fujitani and Komura2013). The mixture is assumed to be incompressible, as in the previous studies mentioned above (Folk & Moser Reference Folk and Moser1998; Onuki Reference Onuki2002). This assumption usually works well in a near-critical mixture prepared experimentally (Anisimov et al. Reference Anisimov, Gorodetskii, Klikov and Sengers1995; Onuki Reference Onuki2002; Pérez-Sanchez et al. Reference Pérez-Sanchez, Losada-Pérez, Cerdeiriña, Sengers and Anisimov2010). When the viscosity is homogeneous, the magnitude of the force is proportional to the particle speed. The constant of proportionality (the drag coefficient) is given by Stokes’ law (Stokes Reference Stokes1851) and is linked with the self-diffusion coefficient of its Brownian motion through the Sutherland–Einstein relation (Einstein Reference Einstein1905; Sutherland Reference Sutherland1905), although the Brownian motion is not always translational. This relation can be derived from the Langevin equation for the particle velocity (Bian, Kim & Karniadakis Reference Bian, Kim and Karniadakis2016), and is further founded on the fluctuating hydrodynamics (Bedeaux & Mazur Reference Bedeaux and Mazur1974), even near the critical point (Mazur & van der Zwan Reference Mazur and van der Zwan1978). In our problem, the suppression of the viscosity enhancement is locally determined by the inhomogeneous shear around the particle, and the drag coefficient can depend on the particle speed in its range to be considered in the Brownian motion. Neither Stokes’ law nor the Sutherland–Einstein relation is applicable when the suppression occurs. Assuming the suppression to remain weak even if it is brought about by the local strong shear, we calculate the drag coefficient. In § 2.4, we use a one-dimensional Langevin equation to link the drag coefficient with the self-diffusion coefficient. Our results are shown and discussed in § 3, and summarized in § 4.
2. Formulation and calculation
We write ![]() $d$ for the spatial dimension; our calculations in the text are limited to the case of
$d$ for the spatial dimension; our calculations in the text are limited to the case of ![]() $d=3$. The values of the static critical exponents are shown in Pelisetto & Vicari (Reference Pelisetto and Vicari2002); we use
$d=3$. The values of the static critical exponents are shown in Pelisetto & Vicari (Reference Pelisetto and Vicari2002); we use ![]() $\nu \approx 0.630$ and
$\nu \approx 0.630$ and ![]() $\eta \approx 0.0364$. The exponent
$\eta \approx 0.0364$. The exponent ![]() $\eta$ represents the deviation from the straightforward dimensional analysis of the static, or equal time, correlation function of the order-parameter fluctuation at the critical point. When the shear is not so strong as to suppress the critical enhancement, the correlation length
$\eta$ represents the deviation from the straightforward dimensional analysis of the static, or equal time, correlation function of the order-parameter fluctuation at the critical point. When the shear is not so strong as to suppress the critical enhancement, the correlation length ![]() $\xi$ is homogeneously given by
$\xi$ is homogeneously given by ![]() $\xi =\xi _0\tau ^{-\nu }$ on the critical isochore, where
$\xi =\xi _0\tau ^{-\nu }$ on the critical isochore, where ![]() $\tau$ is defined as
$\tau$ is defined as ![]() $|T-T_{c}|/T_{c}$ and
$|T-T_{c}|/T_{c}$ and ![]() $\xi _0$ is a non-universal constant. Then, the singular part of the shear viscosity is proportional to
$\xi _0$ is a non-universal constant. Then, the singular part of the shear viscosity is proportional to ![]() $\tau ^{\nu (d-z)}$ in a flow whose typical length is much larger than
$\tau ^{\nu (d-z)}$ in a flow whose typical length is much larger than ![]() $\xi$, as described at (A 2). This exponent is measured to be around
$\xi$, as described at (A 2). This exponent is measured to be around ![]() $-0.042$ (Berg & Moldover Reference Berg and Moldover1989, Reference Berg and Moldover1990), which leads to
$-0.042$ (Berg & Moldover Reference Berg and Moldover1989, Reference Berg and Moldover1990), which leads to ![]() $z=3.067$. Because
$z=3.067$. Because ![]() $|\nu (d-z)|$ is small, the viscosity exhibits a very weak critical singularity. Thus, for the viscosity, the dependence of the regular part on
$|\nu (d-z)|$ is small, the viscosity exhibits a very weak critical singularity. Thus, for the viscosity, the dependence of the regular part on ![]() $\tau$ is also significant unless the mixture is very close to the critical point, unlike for the Onsager coefficient of the interdiffusion. As in Beysens (Reference Beysens2019), we use
$\tau$ is also significant unless the mixture is very close to the critical point, unlike for the Onsager coefficient of the interdiffusion. As in Beysens (Reference Beysens2019), we use
as the viscosity free from the shear effects. In this form of multiplicative anomaly, the regular part ![]() $\tilde {\eta }_{B}$ is defined as
$\tilde {\eta }_{B}$ is defined as
where ![]() $\tilde {\eta }_0$ is a non-universal constant and
$\tilde {\eta }_0$ is a non-universal constant and ![]() $E_{a}$ denotes the activation energy (Sengers Reference Sengers1985; Mehrotra, Monnery & Svrcek Reference Mehrotra, Monnery and Svrcek1996). Molecules would be required to overcome some energy barrier to shift their locations in a dense liquid. Equation (2.1) supposes
$E_{a}$ denotes the activation energy (Sengers Reference Sengers1985; Mehrotra, Monnery & Svrcek Reference Mehrotra, Monnery and Svrcek1996). Molecules would be required to overcome some energy barrier to shift their locations in a dense liquid. Equation (2.1) supposes ![]() $\tau <1$ and the singular part represents the enhancement.
$\tau <1$ and the singular part represents the enhancement.
We define ![]() $\tau _s$ so that a given shear rate
$\tau _s$ so that a given shear rate ![]() ${s}$ affects the critical enhancement for
${s}$ affects the critical enhancement for ![]() $\tau <\tau _s$, and define
$\tau <\tau _s$, and define ![]() $s^*$ so that
$s^*$ so that
holds. Because of (1.1) and (1.3), ![]() $s^*$ is independent of the imposed shear. We will later apply our results to a mixture of isobutyric acid and water. For this mixture under no shear, measured values of
$s^*$ is independent of the imposed shear. We will later apply our results to a mixture of isobutyric acid and water. For this mixture under no shear, measured values of ![]() $\varGamma _k/k^2$ for small
$\varGamma _k/k^2$ for small ![]() $k$ in the neighbourhood of the critical point are shown in figure 10 of Chu, Schoenes & Kao (Reference Chu, Schoenes and Kao1968). These values and
$k$ in the neighbourhood of the critical point are shown in figure 10 of Chu, Schoenes & Kao (Reference Chu, Schoenes and Kao1968). These values and ![]() $\xi _0=0.3625\ \textrm {nm}$ (Beysens, Bourgou & Calmettes Reference Beysens, Bourgou and Calmettes1985) give
$\xi _0=0.3625\ \textrm {nm}$ (Beysens, Bourgou & Calmettes Reference Beysens, Bourgou and Calmettes1985) give ![]() $s^*=3.7\times 10^8\ \textrm {s}^{-1}$ with the aid of (A 4) and (A 6).
$s^*=3.7\times 10^8\ \textrm {s}^{-1}$ with the aid of (A 4) and (A 6).
From § 2.1 to § 2.3, we calculate the drag coefficient of a spherical rigid particle with radius ![]() $r_0$, by assuming it to move translationally with the velocity
$r_0$, by assuming it to move translationally with the velocity ![]() $U\boldsymbol {e}_z$ in a binary fluid mixture in the absence of the preferential adsorption (figure 1). Here,
$U\boldsymbol {e}_z$ in a binary fluid mixture in the absence of the preferential adsorption (figure 1). Here, ![]() $\boldsymbol {e}_z$ denotes a unit vector. The mixture is on the critical isochore in the homogeneous phase with
$\boldsymbol {e}_z$ denotes a unit vector. The mixture is on the critical isochore in the homogeneous phase with ![]() $T$ being close to
$T$ being close to ![]() $T_{c}$, and is quiescent far from the particle. Assuming
$T_{c}$, and is quiescent far from the particle. Assuming ![]() $\xi$ to be much smaller than a typical length scale that the flow changes, we regard the local velocity field as a linear shear flow having the same velocity gradient to determine the local viscosity.
$\xi$ to be much smaller than a typical length scale that the flow changes, we regard the local velocity field as a linear shear flow having the same velocity gradient to determine the local viscosity.

Figure 1. A drawing of a situation for our calculation of the drag coefficient from § 2.1 to § 2.3. A particle with the radius ![]() $r_0$ moves translationally with the velocity
$r_0$ moves translationally with the velocity ![]() $U\boldsymbol {e}_z$ in a mixture fluid quiescent far from the particle. A part of a cross-section containing the
$U\boldsymbol {e}_z$ in a mixture fluid quiescent far from the particle. A part of a cross-section containing the ![]() $z$ axis is shown; the dashed curve represents half of the cross-section of the particle surface. The velocity field, represented by arrows outside the particle, is calculated with a homogeneous viscosity, although the viscosity becomes inhomogeneous when the suppression of the critical enhancement occurs somewhere. A magnified view of the smaller rectangular region is given in the larger one, where clusters are schematically drawn in black and white with some being deformed by the local shear. The correlation length
$z$ axis is shown; the dashed curve represents half of the cross-section of the particle surface. The velocity field, represented by arrows outside the particle, is calculated with a homogeneous viscosity, although the viscosity becomes inhomogeneous when the suppression of the critical enhancement occurs somewhere. A magnified view of the smaller rectangular region is given in the larger one, where clusters are schematically drawn in black and white with some being deformed by the local shear. The correlation length ![]() $\xi$ is assumed to be sufficiently small as compared with a typical length of the flow.
$\xi$ is assumed to be sufficiently small as compared with a typical length of the flow.
2.1. Assumption on the viscosity
We assume that the suppression of the critical enhancement of ![]() $\tilde {\eta }$ is perfect if it occurs, and thus the viscosity is assumed to be given by
$\tilde {\eta }$ is perfect if it occurs, and thus the viscosity is assumed to be given by
 \begin{equation} \tilde{\eta}=\begin{cases} \tilde{\eta}_{B}(T) \tau^{\nu (d-z)} & \textrm{for}\ \tau>\tau_s,\\ \tilde{\eta}_{B}(T) \tau_s^{\nu (d-z)} & \textrm{for}\ \tau< \tau_s, \end{cases}\end{equation}
\begin{equation} \tilde{\eta}=\begin{cases} \tilde{\eta}_{B}(T) \tau^{\nu (d-z)} & \textrm{for}\ \tau>\tau_s,\\ \tilde{\eta}_{B}(T) \tau_s^{\nu (d-z)} & \textrm{for}\ \tau< \tau_s, \end{cases}\end{equation}
which supposes ![]() $\tau <1$ and
$\tau <1$ and ![]() $\tau _s<1$ because (2.1) underlies (2.4). This assumption is discussed in § 3. We write
$\tau _s<1$ because (2.1) underlies (2.4). This assumption is discussed in § 3. We write ![]() $\tilde {\eta }^{(0)}$ for (2.1), and define
$\tilde {\eta }^{(0)}$ for (2.1), and define ![]() $\tilde {\eta }^{(1)}$ so that
$\tilde {\eta }^{(1)}$ so that ![]() $\tilde {\eta }=\tilde {\eta }^{(0)}+\tilde {\eta }^{(1)}$ holds. Introducing
$\tilde {\eta }=\tilde {\eta }^{(0)}+\tilde {\eta }^{(1)}$ holds. Introducing ![]() $\check {\tau }_s\equiv \tau _s/\tau$, we have
$\check {\tau }_s\equiv \tau _s/\tau$, we have
where ![]() $\varTheta$ denotes the step function;
$\varTheta$ denotes the step function; ![]() $\varTheta (x)$ vanishes for
$\varTheta (x)$ vanishes for ![]() $x<0$ and equals unity for
$x<0$ and equals unity for ![]() $x>0$. The shear rate is inhomogeneous, as shown later. Thus, the suppression makes the viscosity inhomogeneous. Subtracting the homogeneous part
$x>0$. The shear rate is inhomogeneous, as shown later. Thus, the suppression makes the viscosity inhomogeneous. Subtracting the homogeneous part ![]() $\tilde {\eta }^{(0)}$ from the whole viscosity
$\tilde {\eta }^{(0)}$ from the whole viscosity ![]() $\tilde {\eta }$ gives
$\tilde {\eta }$ gives ![]() $\tilde {\eta }^{(1)}$, which is non-positive because of
$\tilde {\eta }^{(1)}$, which is non-positive because of ![]() $d=3<z$.
$d=3<z$.
The velocity and pressure fields, ![]() $\boldsymbol {v}$ and
$\boldsymbol {v}$ and ![]() $p$, satisfy the incompressibility condition and Stokes’ equation, i.e.
$p$, satisfy the incompressibility condition and Stokes’ equation, i.e.
where ![]() $\boldsymbol{\boldsymbol{\mathsf{E}}}$ is the rate-of-strain tensor. Here, a low Reynolds number is assumed, as discussed in § 2 of Yabunaka & Fujitani (Reference Yabunaka and Fujitani2020). The no-slip boundary condition is imposed at the particle surface, while
$\boldsymbol{\boldsymbol{\mathsf{E}}}$ is the rate-of-strain tensor. Here, a low Reynolds number is assumed, as discussed in § 2 of Yabunaka & Fujitani (Reference Yabunaka and Fujitani2020). The no-slip boundary condition is imposed at the particle surface, while ![]() $\boldsymbol {v}$ tends to zero and
$\boldsymbol {v}$ tends to zero and ![]() $p$ approaches a constant, denoted by
$p$ approaches a constant, denoted by ![]() $p_{\infty }$, far from the particle.
$p_{\infty }$, far from the particle.
2.2. Approximation for a weak suppression
We consider a particular time and take the spherical coordinates ![]() $(r,\theta ,\phi )$ so that the origin is at the particle's centre and that the polar axis (
$(r,\theta ,\phi )$ so that the origin is at the particle's centre and that the polar axis (![]() $z$ axis) is along
$z$ axis) is along ![]() $\boldsymbol {e}_z$; the coordinate
$\boldsymbol {e}_z$; the coordinate ![]() $z$ should not be confused with the dynamic critical exponent. The unit vectors in the directions of
$z$ should not be confused with the dynamic critical exponent. The unit vectors in the directions of ![]() $r$ and
$r$ and ![]() $\theta$ are denoted by
$\theta$ are denoted by ![]() $\boldsymbol {e}_r$ and
$\boldsymbol {e}_r$ and ![]() $\boldsymbol {e}_{\theta }$, respectively. The no-slip condition gives
$\boldsymbol {e}_{\theta }$, respectively. The no-slip condition gives ![]() $\boldsymbol {v}=U\boldsymbol {e}_z$ at
$\boldsymbol {v}=U\boldsymbol {e}_z$ at ![]() $\rho =1$, where
$\rho =1$, where ![]() $\rho$ denotes a dimensionless radial distance,
$\rho$ denotes a dimensionless radial distance, ![]() $r/r_0$. We can assume
$r/r_0$. We can assume ![]() $v_{\phi }=0$. The drag force is along the
$v_{\phi }=0$. The drag force is along the ![]() $z$ axis; its
$z$ axis; its ![]() $z$ component, denoted by
$z$ component, denoted by ![]() $\mathcal {F}_z$, is given by the surface integral of
$\mathcal {F}_z$, is given by the surface integral of ![]() $(2\tilde {\eta } \boldsymbol{\boldsymbol{\mathsf{E}}} \boldsymbol {\cdot } \boldsymbol {e}_r - p\boldsymbol {e}_r)\boldsymbol {\cdot }\boldsymbol {e}_z$ over the particle surface. The drag coefficient is given by
$(2\tilde {\eta } \boldsymbol{\boldsymbol{\mathsf{E}}} \boldsymbol {\cdot } \boldsymbol {e}_r - p\boldsymbol {e}_r)\boldsymbol {\cdot }\boldsymbol {e}_z$ over the particle surface. The drag coefficient is given by ![]() $-\mathcal {F}_z/U$, and can depend on
$-\mathcal {F}_z/U$, and can depend on ![]() $U$ in our problem. Thus, we write
$U$ in our problem. Thus, we write ![]() $\gamma (U)$ for the drag coefficient.
$\gamma (U)$ for the drag coefficient.
We, respectively, write ![]() $\boldsymbol {v}^{(0)}$ and
$\boldsymbol {v}^{(0)}$ and ![]() $p^{(0)}$ for the velocity and pressure fields obtained when the viscosity is forced to be
$p^{(0)}$ for the velocity and pressure fields obtained when the viscosity is forced to be ![]() $\tilde {\eta }^{(0)}$ homogeneously. Equation (2.6a,b) yields
$\tilde {\eta }^{(0)}$ homogeneously. Equation (2.6a,b) yields
The boundary conditions are ![]() $\boldsymbol {v}^{(0)}=U\boldsymbol {e}_z$ at
$\boldsymbol {v}^{(0)}=U\boldsymbol {e}_z$ at ![]() $\rho =1$, and
$\rho =1$, and ![]() $\boldsymbol {v}^{(0)}\to \boldsymbol {0}$ and
$\boldsymbol {v}^{(0)}\to \boldsymbol {0}$ and ![]() $p^{(0)}\to p_{\infty }$ as
$p^{(0)}\to p_{\infty }$ as ![]() $\rho \to \infty$. The solution is well known (Stokes Reference Stokes1851) and is given by
$\rho \to \infty$. The solution is well known (Stokes Reference Stokes1851) and is given by
and ![]() $v_{\phi }^{(0)}=0$. The arrows outside the particle in figure 1 represent
$v_{\phi }^{(0)}=0$. The arrows outside the particle in figure 1 represent ![]() $\boldsymbol {v}^{(0)}$ for
$\boldsymbol {v}^{(0)}$ for ![]() $U>0$. The superscript
$U>0$. The superscript ![]() ${(0)}$ is also added to a quantity calculated from
${(0)}$ is also added to a quantity calculated from ![]() $\boldsymbol {v}^{(0)}$ and
$\boldsymbol {v}^{(0)}$ and ![]() $p^{(0)}$. The drag coefficient calculated from (2.8a–c) is given by
$p^{(0)}$. The drag coefficient calculated from (2.8a–c) is given by
which is independent of ![]() $U$ and represents Stokes’ law. We define
$U$ and represents Stokes’ law. We define ![]() $\boldsymbol {v}^{(1)}$ and
$\boldsymbol {v}^{(1)}$ and ![]() $p^{(1)}$ as
$p^{(1)}$ as ![]() $\boldsymbol {v}-\boldsymbol {v}^{(0)}$ and
$\boldsymbol {v}-\boldsymbol {v}^{(0)}$ and ![]() $p-p^{(0)}$, respectively. They satisfy
$p-p^{(0)}$, respectively. They satisfy ![]() $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v}^{(1)}=0$ and
$\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v}^{(1)}=0$ and
The boundary conditions are
 \begin{equation} \left. \begin{gathered} \boldsymbol{v}^{(1)}=\boldsymbol{0} \quad \textrm{at}\ \rho=1 \quad\textrm{and}\\ \boldsymbol{v}^{(1)}\to \boldsymbol{0}\quad \textrm{and}\quad p^{(1)}\to 0\quad \textrm{as}\ \rho\to\infty. \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} \boldsymbol{v}^{(1)}=\boldsymbol{0} \quad \textrm{at}\ \rho=1 \quad\textrm{and}\\ \boldsymbol{v}^{(1)}\to \boldsymbol{0}\quad \textrm{and}\quad p^{(1)}\to 0\quad \textrm{as}\ \rho\to\infty. \end{gathered} \right\} \end{equation} In the flow field of ![]() $\boldsymbol {v}$ and
$\boldsymbol {v}$ and ![]() $p$, we define
$p$, we define ![]() $\kappa$ as the maximum value of a dimensionless ratio
$\kappa$ as the maximum value of a dimensionless ratio ![]() $|\tilde {\eta }^{(1)}/\tilde {\eta }^{(0)}|$. Equation (2.5) is proportional to
$|\tilde {\eta }^{(1)}/\tilde {\eta }^{(0)}|$. Equation (2.5) is proportional to ![]() $\kappa$. From (2.10) and (2.11),
$\kappa$. From (2.10) and (2.11), ![]() $\boldsymbol {v}^{(1)}$ is also proportional to
$\boldsymbol {v}^{(1)}$ is also proportional to ![]() $\kappa$. The particle speed supposed here lies in the range involved in the Brownian motion. We assume that
$\kappa$. The particle speed supposed here lies in the range involved in the Brownian motion. We assume that ![]() $\tau$ is not so small as to cause strong suppression, and assume
$\tau$ is not so small as to cause strong suppression, and assume ![]() $\kappa$ to be so small that the calculation up to the order of
$\kappa$ to be so small that the calculation up to the order of ![]() $\kappa$ makes sense. At this order, (2.10) becomes
$\kappa$ makes sense. At this order, (2.10) becomes
Here, ![]() $s$ contained in
$s$ contained in ![]() $\tilde {\eta }^{(1)}$ is replaced by
$\tilde {\eta }^{(1)}$ is replaced by ![]() $s^{(0)}$, which is the shear rate calculated from
$s^{(0)}$, which is the shear rate calculated from ![]() $\boldsymbol {v}^{(0)}$. Likewise, we can evaluate
$\boldsymbol {v}^{(0)}$. Likewise, we can evaluate ![]() $\kappa$ by using
$\kappa$ by using ![]() $s^{(0)}$ instead of
$s^{(0)}$ instead of ![]() $s$ in (2.5). We define
$s$ in (2.5). We define ![]() $\mathcal {F}_z^{(1)}$ so that
$\mathcal {F}_z^{(1)}$ so that ![]() $\mathcal {F}_z=\mathcal {F}_z^{(0)}+\mathcal {F}_z^{(1)}$ holds. At the order of
$\mathcal {F}_z=\mathcal {F}_z^{(0)}+\mathcal {F}_z^{(1)}$ holds. At the order of ![]() $\kappa$,
$\kappa$, ![]() $\mathcal {F}_z^{(1)}$ equals the surface integral of
$\mathcal {F}_z^{(1)}$ equals the surface integral of
over the particle surface, where ![]() $\boldsymbol{\boldsymbol{\mathsf{E}}}^{(1)}$ is the rate-of-strain tensor for
$\boldsymbol{\boldsymbol{\mathsf{E}}}^{(1)}$ is the rate-of-strain tensor for ![]() $\boldsymbol {v}^{(1)}$ and
$\boldsymbol {v}^{(1)}$ and ![]() $p^{(1)}$.
$p^{(1)}$.
On the ![]() $z$ axis, the components of
$z$ axis, the components of ![]() $\boldsymbol {\nabla } \boldsymbol {v}^{(0)}$ with respect to the Cartesian coordinates
$\boldsymbol {\nabla } \boldsymbol {v}^{(0)}$ with respect to the Cartesian coordinates ![]() $(x,y,z)$ is expressed by
$(x,y,z)$ is expressed by ![]() $\partial _zv^{(0)}_z$ multiplied by a traceless diagonal matrix, whose diagonal elements are
$\partial _zv^{(0)}_z$ multiplied by a traceless diagonal matrix, whose diagonal elements are ![]() $-1/2, -1/2$ and
$-1/2, -1/2$ and ![]() $1$ from the top. Here,
$1$ from the top. Here, ![]() $\partial _z$ indicates the partial derivative with respect to
$\partial _z$ indicates the partial derivative with respect to ![]() $z$. Thus, noting the description at the end of the preface of § 2, we can regard
$z$. Thus, noting the description at the end of the preface of § 2, we can regard ![]() $\boldsymbol {v}^{(0)}$ on the
$\boldsymbol {v}^{(0)}$ on the ![]() $z$ axis as a pure-extension flow locally. In particular, at a point with
$z$ axis as a pure-extension flow locally. In particular, at a point with ![]() $\theta ={\rm \pi}$ for
$\theta ={\rm \pi}$ for ![]() $U>0$, the largest stretching rate occurs in the
$U>0$, the largest stretching rate occurs in the ![]() $z$ direction, i.e. the radial direction, and is given by
$z$ direction, i.e. the radial direction, and is given by ![]() $\partial _r v^{(0)}_r$. As
$\partial _r v^{(0)}_r$. As ![]() $\theta$ approaches
$\theta$ approaches ![]() ${\rm \pi} /2$, periodic motion becomes predominant over elongational motion in
${\rm \pi} /2$, periodic motion becomes predominant over elongational motion in ![]() $\boldsymbol {v}^{(0)}$, as is suggested by figure 1 and is explicitly shown in appendix B. A rotational flow is found to be weak in suppressing the critical enhancement (Onuki & Kawasaki Reference Onuki and Kawasaki1980c). Thus, considering the discussion on the elongational flow in the fourth paragraph of § 1, we assume that
$\boldsymbol {v}^{(0)}$, as is suggested by figure 1 and is explicitly shown in appendix B. A rotational flow is found to be weak in suppressing the critical enhancement (Onuki & Kawasaki Reference Onuki and Kawasaki1980c). Thus, considering the discussion on the elongational flow in the fourth paragraph of § 1, we assume that ![]() $s^{(0)}$ is given by the largest real-part of the eigenvalues of
$s^{(0)}$ is given by the largest real-part of the eigenvalues of ![]() $\boldsymbol {\nabla }\boldsymbol {v}^{(0)}$. Calculating them directly from (2.8a–c), we find
$\boldsymbol {\nabla }\boldsymbol {v}^{(0)}$. Calculating them directly from (2.8a–c), we find ![]() $s^{(0)}$ to be given by
$s^{(0)}$ to be given by
where a positive factor ![]() ${c}$, depending on
${c}$, depending on ![]() $\theta$, ranges from
$\theta$, ranges from ![]() $1/2$ to
$1/2$ to ![]() $2$. Equation (2.14) with
$2$. Equation (2.14) with ![]() ${c}=2$ equals
${c}=2$ equals ![]() $\vert \partial _r v^{(0)}_r\vert$. We proceed below with calculations by regarding
$\vert \partial _r v^{(0)}_r\vert$. We proceed below with calculations by regarding ![]() ${c}$ as a constant, in spite of the actual dependence of
${c}$ as a constant, in spite of the actual dependence of ![]() $c$ on
$c$ on ![]() $\theta$. It will be shown later that our result of the self-diffusion coefficient is rather insensitive to the value of
$\theta$. It will be shown later that our result of the self-diffusion coefficient is rather insensitive to the value of ![]() ${c}$.
${c}$.
2.3. Expansions with respect to the spherical harmonics
The flow we consider here is symmetric with respect to the polar axis, and thus the angular part of ![]() $\boldsymbol {v}^{(1)}$ can be expanded in terms of the vector spherical harmonics,
$\boldsymbol {v}^{(1)}$ can be expanded in terms of the vector spherical harmonics,
for ![]() $J=1,2,\ldots$ (Morse & Feshbach Reference Morse and Feshbach1953; Barrera, Estévez & Giraldo Reference Barrera, Estévez and Giraldo1985; Fujitani Reference Fujitani2007). Here,
$J=1,2,\ldots$ (Morse & Feshbach Reference Morse and Feshbach1953; Barrera, Estévez & Giraldo Reference Barrera, Estévez and Giraldo1985; Fujitani Reference Fujitani2007). Here, ![]() $Y_{J0}(\theta )$ is one of the spherical harmonics,
$Y_{J0}(\theta )$ is one of the spherical harmonics, ![]() $\sqrt {(2J+1)/(4{\rm \pi} )}P_J(\cos {\theta })$, with
$\sqrt {(2J+1)/(4{\rm \pi} )}P_J(\cos {\theta })$, with ![]() $P_J$ denoting the Legendre polynomial, e.g.
$P_J$ denoting the Legendre polynomial, e.g. ![]() $P_1(x)=x$. The mode
$P_1(x)=x$. The mode ![]() $J=0$ need not be considered because of the incompressibility. We define functions
$J=0$ need not be considered because of the incompressibility. We define functions ![]() $\varPi _J$,
$\varPi _J$, ![]() $R_J$ and
$R_J$ and ![]() $T_J$ so that
$T_J$ so that
hold. We expand the negative of the right-hand side of (2.12) as
whereby ![]() $F_J$ and
$F_J$ and ![]() $H_J$ are defined. They are obtained with the aid of the orthogonality of the vector spherical harmonics. The incompressibility condition gives
$H_J$ are defined. They are obtained with the aid of the orthogonality of the vector spherical harmonics. The incompressibility condition gives
We use (2.18) to delete ![]() $T_J$ from the
$T_J$ from the ![]() $r$ and
$r$ and ![]() $\theta$ components of (2.12), which are combined to give
$\theta$ components of (2.12), which are combined to give
Here, ![]() $X_J$ is defined as
$X_J$ is defined as
Similar calculations can be found in deriving (2.17) of Fujitani (Reference Fujitani2007) and in deriving (3.20) of Yabunaka & Fujitani (Reference Yabunaka and Fujitani2020). Equations (2.11) and (2.18) give
Applying the method of variation of parameters, we can rewrite (2.19) as
where the kernel ![]() $\varGamma_{J}$ is given in appendix C.
$\varGamma_{J}$ is given in appendix C.
The first term of (2.13) does not contribute to ![]() $\mathcal {F}_z^{(1)}$ because (2.14), and thus (2.5), vanish at the particle surface. With the aid of (2.18), we use the
$\mathcal {F}_z^{(1)}$ because (2.14), and thus (2.5), vanish at the particle surface. With the aid of (2.18), we use the ![]() $\theta$ component of (2.12) to delete
$\theta$ component of (2.12) to delete ![]() $\varPi _J$ and
$\varPi _J$ and ![]() $T_J$ from the last two terms of (2.13). These terms are thus rewritten as the sum of terms involving
$T_J$ from the last two terms of (2.13). These terms are thus rewritten as the sum of terms involving ![]() $R_J$ and
$R_J$ and ![]() $H_J$ over
$H_J$ over ![]() $J$. Only the terms involving
$J$. Only the terms involving ![]() $R_1$ are left after the surface integration of (2.13), as shown by (C 4) and described below (C 5). Substituting (2.22) into the result of the surface integration, we use
$R_1$ are left after the surface integration of (2.13), as shown by (C 4) and described below (C 5). Substituting (2.22) into the result of the surface integration, we use
The right-hand side above is related to the fraction appearing in (2.8b) because of the Lorentz reciprocal theorem (Lorentz Reference Lorentz1896), as shown in appendix B of Fujitani (Reference Fujitani2018) and mentioned at (A2) of Yabunaka & Fujitani (Reference Yabunaka and Fujitani2020). We thus arrive at
where ![]() $\check {X}$ is defined as
$\check {X}$ is defined as
As shown by (C 7), ![]() $\check {X}$ is given in terms of the integral with respect to
$\check {X}$ is given in terms of the integral with respect to ![]() $\theta$ because (2.20) involves
$\theta$ because (2.20) involves ![]() $F_1$ and
$F_1$ and ![]() $H_1$, which are calculated from the right-hand side of (2.12) with the aid of the orthogonality of the vector spherical harmonics. Thus, (2.24) contains a double integral with respect to
$H_1$, which are calculated from the right-hand side of (2.12) with the aid of the orthogonality of the vector spherical harmonics. Thus, (2.24) contains a double integral with respect to ![]() $\rho$ and
$\rho$ and ![]() $\theta$. We have analytical results for the integrals with respect to
$\theta$. We have analytical results for the integrals with respect to ![]() $\rho$, as described at the end of appendix C, and thus what to calculate numerically is the integration with respect to
$\rho$, as described at the end of appendix C, and thus what to calculate numerically is the integration with respect to ![]() $\theta$.
$\theta$.
We find ![]() $\check {X}$ to depend on
$\check {X}$ to depend on ![]() $U$ only through
$U$ only through ![]() $\tau _{s^{(0)}}$. With
$\tau _{s^{(0)}}$. With ![]() $U^*$ denoting
$U^*$ denoting ![]() $s^*r_0$, the ratio
$s^*r_0$, the ratio ![]() $\gamma (U)/\gamma ^{(0)} = 1+(\mathcal {F}_z^{(1)}/\mathcal {F}_z^{(0)})$ is a function of a dimensionless speed
$\gamma (U)/\gamma ^{(0)} = 1+(\mathcal {F}_z^{(1)}/\mathcal {F}_z^{(0)})$ is a function of a dimensionless speed ![]() $|U|/U^*$ because of (2.3) and (2.14), and is denoted by
$|U|/U^*$ because of (2.3) and (2.14), and is denoted by ![]() $\check {\gamma }(U/U^*)$. Using the value of the critical exponents stated in the preface of § 2, we numerically calculate the integral of (2.24) to obtain
$\check {\gamma }(U/U^*)$. Using the value of the critical exponents stated in the preface of § 2, we numerically calculate the integral of (2.24) to obtain ![]() $\check {\gamma }(u)$. In figure 2,
$\check {\gamma }(u)$. In figure 2, ![]() $\check {\gamma }(u)$ decreases as
$\check {\gamma }(u)$ decreases as ![]() $u$ increases, which represents that the critical enhancement of
$u$ increases, which represents that the critical enhancement of ![]() $\tilde {\eta }$ is suppressed more as the faster particle causes stronger shear. At the smaller value of
$\tilde {\eta }$ is suppressed more as the faster particle causes stronger shear. At the smaller value of ![]() $\tau$, the suppression is shown to be stronger, which can be explained by the existence of larger clusters deformable for smaller
$\tau$, the suppression is shown to be stronger, which can be explained by the existence of larger clusters deformable for smaller ![]() $u$.
$u$.

Figure 2. We plot ![]() $\check {\gamma }(u)$ for
$\check {\gamma }(u)$ for ![]() $\tau =1.008\times 10^{-3}\ (\circ )$ and
$\tau =1.008\times 10^{-3}\ (\circ )$ and ![]() $1.26\times 10^{-4}\ (+)$. As mentioned in the text,
$1.26\times 10^{-4}\ (+)$. As mentioned in the text, ![]() $\check {\gamma }$ represents the drag coefficient non-dimensionalized by (2.9), while
$\check {\gamma }$ represents the drag coefficient non-dimensionalized by (2.9), while ![]() $u$ represents the particle speed non-dimensionalized by
$u$ represents the particle speed non-dimensionalized by ![]() $U^{\ast }\equiv s^{\ast } r_0$.
$U^{\ast }\equiv s^{\ast } r_0$.
2.4. Description of the Brownian motion
When the viscosity is homogeneous in the absence of the suppression, as mentioned in § 1, a simple description of the Brownian motion is given by the Langevin equation for the particle velocity, where the force exerted on the particle is separated into the thermal noise and the instantaneous friction force (Bian et al. Reference Bian, Kim and Karniadakis2016). The former represents the force varying much more rapidly than the latter and vanishes after being averaged over a macroscopic time interval (Sekimoto Reference Sekimoto2010), while the friction coefficient in the latter equals the drag coefficient given by Stokes’ law. This is founded in terms of the fluctuating hydrodynamics (Bedeaux & Mazur Reference Bedeaux and Mazur1974; Mazur & van der Zwan Reference Mazur and van der Zwan1978) and is numerically verified (Keblinski & Thomin Reference Keblinski and Thomin2006). The components of the thermal noise in the three orthogonal directions are statistically independent, and thus the self-diffusion coefficient can be calculated in one dimension. To calculate the self-diffusion coefficient in our problem, we still use the drag coefficient ![]() $\gamma (U)$ as the friction coefficient in the Langevin equation, considering that the viscosity can be only weakly inhomogeneous depending on the particle speed. This amounts to assuming
$\gamma (U)$ as the friction coefficient in the Langevin equation, considering that the viscosity can be only weakly inhomogeneous depending on the particle speed. This amounts to assuming ![]() $\gamma (U)$ to be most probable friction coefficient when the particle velocity is
$\gamma (U)$ to be most probable friction coefficient when the particle velocity is ![]() $U$ in the Brownian motion at the time resolution of the Langevin equation.
$U$ in the Brownian motion at the time resolution of the Langevin equation.
The effective mass, denoted by ![]() $m$, is the sum of the particle mass and half the mass of the displaced fluid (Lamb Reference Lamb1932; Bian et al. Reference Bian, Kim and Karniadakis2016; Fujitani Reference Fujitani2018). Here, unlike in the preceding subsections,
$m$, is the sum of the particle mass and half the mass of the displaced fluid (Lamb Reference Lamb1932; Bian et al. Reference Bian, Kim and Karniadakis2016; Fujitani Reference Fujitani2018). Here, unlike in the preceding subsections, ![]() $U$ is a stochastic variable depending on the time
$U$ is a stochastic variable depending on the time ![]() $t$. The Langevin equation is
$t$. The Langevin equation is
where ![]() $W$ represents the Wiener process and the symbol
$W$ represents the Wiener process and the symbol ![]() $\circ$ indicates that (2.26) should be interpreted in the Stratonovich sense (Risken Reference Risken2002; Sekimoto Reference Sekimoto2010). The positive function
$\circ$ indicates that (2.26) should be interpreted in the Stratonovich sense (Risken Reference Risken2002; Sekimoto Reference Sekimoto2010). The positive function ![]() $b(U)$ is fixed so that (2.26) is consistent with the Boltzmann distribution, as shown in appendix D. The self-diffusion coefficient of the particle
$b(U)$ is fixed so that (2.26) is consistent with the Boltzmann distribution, as shown in appendix D. The self-diffusion coefficient of the particle ![]() $D$ is given by (Bian et al. Reference Bian, Kim and Karniadakis2016)
$D$ is given by (Bian et al. Reference Bian, Kim and Karniadakis2016)
where ![]() $\langle \cdots \rangle$ means the equilibrium average. Defining
$\langle \cdots \rangle$ means the equilibrium average. Defining ![]() $M$ as
$M$ as ![]() $mU^{*2}/(k_{B}T)$, we utilize the Laplace transformation to obtain
$mU^{*2}/(k_{B}T)$, we utilize the Laplace transformation to obtain
as shown in appendix D. This equation can be also derived from (2.26) by using not the Laplace transformation but some of the equations in § S.9 of Risken (Reference Risken2002). Converting the integration variables ![]() $u$ and
$u$ and ![]() $u_1$ to
$u_1$ to ![]() $u\sqrt {M}$ and
$u\sqrt {M}$ and ![]() $u_1\sqrt {M}$, respectively, we find that
$u_1\sqrt {M}$, respectively, we find that ![]() $D$ depends on
$D$ depends on ![]() $M$ only through the variable of
$M$ only through the variable of ![]() $\check {\gamma }$.
$\check {\gamma }$.
Equation (2.28) involves ![]() $\check {\gamma }(u)$ for infinitely large
$\check {\gamma }(u)$ for infinitely large ![]() $u$ because (2.26) formally supposes any particle speed, including the particle speed larger than assumed in the hydrodynamic formulation. This is also the case with the Langevin equation supposing a constant drag coefficient, where Stokes’ law is assumed even for particle speeds so large as to break the validity of the Stokes approximation. In either case, we can avoid this inconvenience in computing the self-diffusion coefficient, to which such large speed never contributes. An effective cutoff speed is implicitly imposed on the Langevin equation. This point is discussed in the next section.
$u$ because (2.26) formally supposes any particle speed, including the particle speed larger than assumed in the hydrodynamic formulation. This is also the case with the Langevin equation supposing a constant drag coefficient, where Stokes’ law is assumed even for particle speeds so large as to break the validity of the Stokes approximation. In either case, we can avoid this inconvenience in computing the self-diffusion coefficient, to which such large speed never contributes. An effective cutoff speed is implicitly imposed on the Langevin equation. This point is discussed in the next section.
3. Results and discussion
Latex beads with radius ![]() $80\ \textrm {nm}$ are put in a mixture of isobutyric acid and water in the experiment of Beysens (Reference Beysens2019), where we have
$80\ \textrm {nm}$ are put in a mixture of isobutyric acid and water in the experiment of Beysens (Reference Beysens2019), where we have ![]() $m=3.32\times 10^{-18}\ \textrm {kg}$ and
$m=3.32\times 10^{-18}\ \textrm {kg}$ and ![]() $U^*=29.6\ \textrm {m}\ \textrm {s}^{-1}$. The mixture can be regarded as incompressible near the demixing critical point (Clerke & Sengers Reference Clerke and Sengers1983; Onuki Reference Onuki2002). The thermal average of
$U^*=29.6\ \textrm {m}\ \textrm {s}^{-1}$. The mixture can be regarded as incompressible near the demixing critical point (Clerke & Sengers Reference Clerke and Sengers1983; Onuki Reference Onuki2002). The thermal average of ![]() $U$ is
$U$ is ![]() $3.53\times 10^{-2}\ \textrm {m}\ \textrm {s}^{-1}$, which is denoted by
$3.53\times 10^{-2}\ \textrm {m}\ \textrm {s}^{-1}$, which is denoted by ![]() $\bar {U}$. The improper integrals in (2.28) can be replaced by definite integrals involving only particle speeds smaller than approximately
$\bar {U}$. The improper integrals in (2.28) can be replaced by definite integrals involving only particle speeds smaller than approximately ![]() $4\bar {U}$, as described in the latter half of appendix D. Because the viscosity of the mixture is around
$4\bar {U}$, as described in the latter half of appendix D. Because the viscosity of the mixture is around ![]() $2.5\times 10^{-3}\ \textrm {kg}\ \textrm {m}^{-1}\ \textrm {s}^{-1}$ (Allegra, Stein & Allen Reference Allegra, Stein and Allen1971), the Reynolds number is
$2.5\times 10^{-3}\ \textrm {kg}\ \textrm {m}^{-1}\ \textrm {s}^{-1}$ (Allegra, Stein & Allen Reference Allegra, Stein and Allen1971), the Reynolds number is ![]() $1.4\times 10^{-2}$ for
$1.4\times 10^{-2}$ for ![]() $U=\bar {U}$, and remains sufficiently small as compared with unity even if multiplied by four. This is consistent with our hydrodynamic formulation. The variable
$U=\bar {U}$, and remains sufficiently small as compared with unity even if multiplied by four. This is consistent with our hydrodynamic formulation. The variable ![]() $u$ in figure 2 represents
$u$ in figure 2 represents ![]() $U/U^*$, which equals
$U/U^*$, which equals ![]() $1.19\times 10^{-3}$ for
$1.19\times 10^{-3}$ for ![]() $U=\bar {U}$. Thus, the range of the horizontal axis in figure 2 approximately coincides with the integration interval of the definite integrals used in our numerical calculation.
$U=\bar {U}$. Thus, the range of the horizontal axis in figure 2 approximately coincides with the integration interval of the definite integrals used in our numerical calculation.
The data of the self-diffusion coefficient in Beysens (Reference Beysens2019), ranging over ![]() $6.31\times 10^{-5}\le \tau \le 6.81\times 10^{-2}$, are replotted with open circles in figure 3. The viscosity of the near-critical mixture of isobutyric acid and water, containing no particles, is measured in Allegra et al. (Reference Allegra, Stein and Allen1971). From the data in their table 2, with the ones for four values of
$6.31\times 10^{-5}\le \tau \le 6.81\times 10^{-2}$, are replotted with open circles in figure 3. The viscosity of the near-critical mixture of isobutyric acid and water, containing no particles, is measured in Allegra et al. (Reference Allegra, Stein and Allen1971). From the data in their table 2, with the ones for four values of ![]() $\tau$ from the smallest being excluded according to Oxtoby (Reference Oxtoby1975), we calculate the self-diffusion coefficient by applying Stokes’ law and the Sutherland–Einstein relation, i.e. by dividing
$\tau$ from the smallest being excluded according to Oxtoby (Reference Oxtoby1975), we calculate the self-diffusion coefficient by applying Stokes’ law and the Sutherland–Einstein relation, i.e. by dividing ![]() $k_{B}T/(6{\rm \pi} r_0)$ by the viscosity, and plot the results with crosses in figure 3. The crosses, ranging over
$k_{B}T/(6{\rm \pi} r_0)$ by the viscosity, and plot the results with crosses in figure 3. The crosses, ranging over ![]() $1.14\times 10^{-4}\le \tau \le 2.78\times 10^{-2}$, agree with the open circles for
$1.14\times 10^{-4}\le \tau \le 2.78\times 10^{-2}$, agree with the open circles for ![]() $\tau >7\times 10^{-3}$. These open circles and the crosses should be explained by using (2.1), i.e.
$\tau >7\times 10^{-3}$. These open circles and the crosses should be explained by using (2.1), i.e. ![]() $\tilde {\eta }^{(0)}$, which is free from the suppression due to the shear.
$\tilde {\eta }^{(0)}$, which is free from the suppression due to the shear.

Figure 3. Plot of the self-diffusion coefficient against ![]() $\tau$. Open circles represent the experimental data of Beysens (Reference Beysens2019), where
$\tau$. Open circles represent the experimental data of Beysens (Reference Beysens2019), where ![]() $T_{c}$ is estimated to be 301.1 K. Crosses come from Allegra et al. (Reference Allegra, Stein and Allen1971), with
$T_{c}$ is estimated to be 301.1 K. Crosses come from Allegra et al. (Reference Allegra, Stein and Allen1971), with ![]() $T_{c}$ being estimated to be 299.4 K. The dashed curve represents
$T_{c}$ being estimated to be 299.4 K. The dashed curve represents ![]() $k_{B}T/(6{\rm \pi} \tilde {\eta }^{(0)}r_0)$, which we calculate by using the parameter values estimated from the open circles for
$k_{B}T/(6{\rm \pi} \tilde {\eta }^{(0)}r_0)$, which we calculate by using the parameter values estimated from the open circles for ![]() $\tau >7\times 10^{-3}$ and the crosses. Solid circles represent our results of (2.28) for
$\tau >7\times 10^{-3}$ and the crosses. Solid circles represent our results of (2.28) for ![]() $c=1$. The red short bar above (below) each of the solid circles for
$c=1$. The red short bar above (below) each of the solid circles for ![]() $\tau \le 1.61\times 10^{-2}$ represents (2.28) for
$\tau \le 1.61\times 10^{-2}$ represents (2.28) for ![]() $c=4\ (0.25)$.
$c=4\ (0.25)$.
Conversely, we can calculate the viscosity from the open circles for ![]() $\tau >7\times 10^{-3}$ by applying Stokes’ law and the Sutherland–Einstein relation. In a graph (not shown here) where these results and the data of Allegra et al. (Reference Allegra, Stein and Allen1971) with the exclusion above are linearly plotted against
$\tau >7\times 10^{-3}$ by applying Stokes’ law and the Sutherland–Einstein relation. In a graph (not shown here) where these results and the data of Allegra et al. (Reference Allegra, Stein and Allen1971) with the exclusion above are linearly plotted against ![]() $\tau$, we perform the curve-fit to
$\tau$, we perform the curve-fit to ![]() $\tilde {\eta }^{(0)}$ with the aid of ‘NonlinearModelFit’ of Mathematica (Wolfram Research) by using
$\tilde {\eta }^{(0)}$ with the aid of ‘NonlinearModelFit’ of Mathematica (Wolfram Research) by using ![]() $T_{c}=300.1\ \textrm {K}$ (Toumi & Bouanz Reference Toumi and Bouanz2008) and the values of the critical exponents stated in the preface of § 2. Estimated values are
$T_{c}=300.1\ \textrm {K}$ (Toumi & Bouanz Reference Toumi and Bouanz2008) and the values of the critical exponents stated in the preface of § 2. Estimated values are ![]() $\tilde {\eta }_0=3.38\times 10^{-6}\ \textrm {kg}\ \textrm {m}\ \textrm {s}^{-1}$ and
$\tilde {\eta }_0=3.38\times 10^{-6}\ \textrm {kg}\ \textrm {m}\ \textrm {s}^{-1}$ and ![]() $E_{a}/(k_{B}T_{c})=6.35$ with the standard deviations being
$E_{a}/(k_{B}T_{c})=6.35$ with the standard deviations being ![]() $5.11\times 10^{-7}\ \textrm {kg}\ \textrm {m}\ \textrm {s}^{-1}$ and
$5.11\times 10^{-7}\ \textrm {kg}\ \textrm {m}\ \textrm {s}^{-1}$ and ![]() $1.53\times 10^{-1}$, respectively. We use the estimated values to calculate
$1.53\times 10^{-1}$, respectively. We use the estimated values to calculate ![]() $\tilde {\gamma }^{(0)}=6{\rm \pi} \tilde {\eta }^{(0)}r_0$ and plot
$\tilde {\gamma }^{(0)}=6{\rm \pi} \tilde {\eta }^{(0)}r_0$ and plot ![]() $k_{B}T/\gamma ^{(0)}$ with the dashed curve in figure 3; the curve agrees well with the data applied to the curve-fit. Employing
$k_{B}T/\gamma ^{(0)}$ with the dashed curve in figure 3; the curve agrees well with the data applied to the curve-fit. Employing ![]() ${\tilde \gamma }^{(0)}$ thus obtained, we calculate the prefactor of (2.28), whose integrals are numerically calculated after being replaced by the definite integrals mentioned above. Our results of
${\tilde \gamma }^{(0)}$ thus obtained, we calculate the prefactor of (2.28), whose integrals are numerically calculated after being replaced by the definite integrals mentioned above. Our results of ![]() $D$ for
$D$ for ![]() $c=1$ are plotted with solid circles in figure 3. It appears that the open circles saturate to reach a plateau as
$c=1$ are plotted with solid circles in figure 3. It appears that the open circles saturate to reach a plateau as ![]() $\tau$ decreases below
$\tau$ decreases below ![]() $3.2\times 10^{-3}$, although they are distributed rather widely in the direction of the vertical axis. Our results pass through the middle of the distribution. This strongly suggests that the saturation should represent the suppression of the critical enhancement of
$3.2\times 10^{-3}$, although they are distributed rather widely in the direction of the vertical axis. Our results pass through the middle of the distribution. This strongly suggests that the saturation should represent the suppression of the critical enhancement of ![]() $\tilde {\eta }$ due to the local shear caused by the particle motion, as claimed by Beysens (Reference Beysens2019).
$\tilde {\eta }$ due to the local shear caused by the particle motion, as claimed by Beysens (Reference Beysens2019).
Figure 4 shows that our calculation results of ![]() $D$ increase as
$D$ increase as ![]() $c$ increases, which can be expected because the shear is then evaluated to be larger. In this figure, the ratios of the change in
$c$ increases, which can be expected because the shear is then evaluated to be larger. In this figure, the ratios of the change in ![]() $D$ lie within
$D$ lie within ![]() $5\,\%$ when
$5\,\%$ when ![]() $c$ changes from unity to
$c$ changes from unity to ![]() $0.1$ or to
$0.1$ or to ![]() $10$; dependences of the ratio on
$10$; dependences of the ratio on ![]() $c$ are almost the same for the two values of
$c$ are almost the same for the two values of ![]() $\tau$. For comparison with the data of Beysens (Reference Beysens2019), we plot (2.28) for
$\tau$. For comparison with the data of Beysens (Reference Beysens2019), we plot (2.28) for ![]() $c=0.25$ and
$c=0.25$ and ![]() $4$ with red short bars in figure 3. It is clear for
$4$ with red short bars in figure 3. It is clear for ![]() $\tau >10^{-3}$ that the two bars at the same
$\tau >10^{-3}$ that the two bars at the same ![]() $\tau$ are closer to each other as
$\tau$ are closer to each other as ![]() $\tau$ is larger; (2.28) depends on
$\tau$ is larger; (2.28) depends on ![]() $c$ only when the suppression occurs. The range of
$c$ only when the suppression occurs. The range of ![]() $c$ is considered as
$c$ is considered as ![]() $1/2\le c\le 2$ in § 2.2. For
$1/2\le c\le 2$ in § 2.2. For ![]() $c=1/2\ (2)$, each of the results indicated by solid circles for
$c=1/2\ (2)$, each of the results indicated by solid circles for ![]() $\tau \le 1.61\times 10^{-2}$ is shifted to the middle between the solid circle and the lower (upper) short bar. These slight shifts show that our results for any value of
$\tau \le 1.61\times 10^{-2}$ is shifted to the middle between the solid circle and the lower (upper) short bar. These slight shifts show that our results for any value of ![]() $c$ in the interval of
$c$ in the interval of ![]() $1/2\le c\le 2$ explain the experimental data well. It is also suggested that, if we take into account the dependence of
$1/2\le c\le 2$ explain the experimental data well. It is also suggested that, if we take into account the dependence of ![]() $c$ on
$c$ on ![]() $\theta$ in this interval, the calculation results should remain in good agreement with the experimental data.
$\theta$ in this interval, the calculation results should remain in good agreement with the experimental data.

Figure 4. Ratios of ![]() $D$ for some
$D$ for some ![]() $c$ values to
$c$ values to ![]() $D$ for
$D$ for ![]() $c=1$ are calculated with the aid of (2.28) and plotted. The values of
$c=1$ are calculated with the aid of (2.28) and plotted. The values of ![]() $\tau$ are
$\tau$ are ![]() $1.26\times 10^{-4}\ (+)$ and
$1.26\times 10^{-4}\ (+)$ and ![]() $1.008\times 10^{-3}\ (\circ )$.
$1.008\times 10^{-3}\ (\circ )$.
Let us examine where the suppression occurs around a particle moving in the way supposed in figure 1. In the approximation mentioned below (2.12), we use ![]() $s^{(0)}$ instead of
$s^{(0)}$ instead of ![]() $s$ in (2.5) to calculate
$s$ in (2.5) to calculate ![]() $|\tilde {\eta }^{(1)}/\tilde {\eta }^{(0)}|$ for
$|\tilde {\eta }^{(1)}/\tilde {\eta }^{(0)}|$ for ![]() $c=1$ and
$c=1$ and ![]() $U=\bar {U}$, and show the results in figure 5, where the suppression occurs in coloured regions. The maximum of (2.14) is taken at
$U=\bar {U}$, and show the results in figure 5, where the suppression occurs in coloured regions. The maximum of (2.14) is taken at ![]() $(\rho , \theta )= (\sqrt {2}, 0)$ or
$(\rho , \theta )= (\sqrt {2}, 0)$ or ![]() $(\sqrt {2},{\rm \pi} )$. The value of
$(\sqrt {2},{\rm \pi} )$. The value of ![]() $\vert \tilde {\eta }^{(1)}/\tilde {\eta }^{(0)}\vert$ equals
$\vert \tilde {\eta }^{(1)}/\tilde {\eta }^{(0)}\vert$ equals ![]() $\kappa$ at these points, and becomes smaller at a point more distant from these points, as shown in figure 5. The maximum of
$\kappa$ at these points, and becomes smaller at a point more distant from these points, as shown in figure 5. The maximum of ![]() ${\tau }_{s^{(0)}}$ is
${\tau }_{s^{(0)}}$ is ![]() $0.0129\times c^{0.518}$ for
$0.0129\times c^{0.518}$ for ![]() $U=\bar {U}$, and is
$U=\bar {U}$, and is ![]() $0.0264\times c^{0.518}$ for
$0.0264\times c^{0.518}$ for ![]() $U=4\bar {U}$, which is approximately the effective cutoff in our numerical integration. The latter yields
$U=4\bar {U}$, which is approximately the effective cutoff in our numerical integration. The latter yields ![]() $\kappa \approx 0.13$ at
$\kappa \approx 0.13$ at ![]() $\tau =10^{-3}$ and
$\tau =10^{-3}$ and ![]() $\approx 0.21$ at
$\approx 0.21$ at ![]() $\tau =10^{-4}$ for
$\tau =10^{-4}$ for ![]() $c=1$ and
$c=1$ and ![]() $U=4\bar {U}$. Thus,
$U=4\bar {U}$. Thus, ![]() $\kappa$ is adequately small as compared with unity in the range of
$\kappa$ is adequately small as compared with unity in the range of ![]() $\tau$ examined in figure 3, which would make our formulation globally meaningful.
$\tau$ examined in figure 3, which would make our formulation globally meaningful.

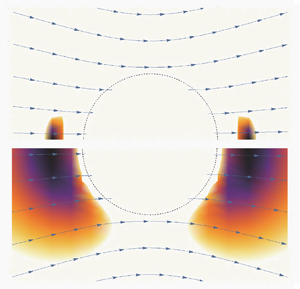
Figure 5. Colour gradation represents the largest of zero and ![]() $1-\check {\tau }_{s^{(0)}}^{\nu (d-z)}$ for
$1-\check {\tau }_{s^{(0)}}^{\nu (d-z)}$ for ![]() $c=1$ and
$c=1$ and ![]() $U=\bar {U}$ at each of
$U=\bar {U}$ at each of ![]() $\tau =1.26\times 10^{-2}$
$\tau =1.26\times 10^{-2}$ ![]() $(a)$ and
$(a)$ and ![]() $8.064\times 10^{-3}$
$8.064\times 10^{-3}$ ![]() $(b)$. The particle is assumed to move translationally with the velocity
$(b)$. The particle is assumed to move translationally with the velocity ![]() $\bar {U}\boldsymbol {e}_z$. The region shown in each figure is the same as in figure 1; the dotted curve represents the half of the cross-section of the particle surface. The curves outside the particle are the stream lines of
$\bar {U}\boldsymbol {e}_z$. The region shown in each figure is the same as in figure 1; the dotted curve represents the half of the cross-section of the particle surface. The curves outside the particle are the stream lines of ![]() $\boldsymbol {v}^{(0)}$, which are represented by arrows in figure 1.
$\boldsymbol {v}^{(0)}$, which are represented by arrows in figure 1.
From the maximum of ![]() ${\tau }_{s^{(0)}}$ for
${\tau }_{s^{(0)}}$ for ![]() $U=\bar {U}$ mentioned above,
$U=\bar {U}$ mentioned above, ![]() $\kappa$ is found to become non-zero when
$\kappa$ is found to become non-zero when ![]() $\tau$ is smaller than
$\tau$ is smaller than ![]() $1.29\times 10^{-2}$ for
$1.29\times 10^{-2}$ for ![]() $c=1$ and
$c=1$ and ![]() $U=\bar {U}$. This value of
$U=\bar {U}$. This value of ![]() $\tau$ approximately agrees with the onset temperature of the suppression estimated in Beysens (Reference Beysens2019), where the shear rate, with its inhomogeneity and dependence on
$\tau$ approximately agrees with the onset temperature of the suppression estimated in Beysens (Reference Beysens2019), where the shear rate, with its inhomogeneity and dependence on ![]() $U$ being neglected, is evaluated to be a typical shear rate,
$U$ being neglected, is evaluated to be a typical shear rate, ![]() $\bar {U}/r_0$. The value of
$\bar {U}/r_0$. The value of ![]() $\tau$ is slightly smaller than
$\tau$ is slightly smaller than ![]() $1.29\times 10^{-2}$ in figure 5(a), where a very weak suppression occurs in narrow regions around
$1.29\times 10^{-2}$ in figure 5(a), where a very weak suppression occurs in narrow regions around ![]() $(\rho , \theta )= (\sqrt {2}, 0)$ and
$(\rho , \theta )= (\sqrt {2}, 0)$ and ![]() $(\sqrt {2},{\rm \pi} )$ for
$(\sqrt {2},{\rm \pi} )$ for ![]() $c=1$ and
$c=1$ and ![]() $U=\bar {U}$, as expected. However, at this temperature, the suppression cannot be read in figure 3. In figure 5(b) with smaller
$U=\bar {U}$, as expected. However, at this temperature, the suppression cannot be read in figure 3. In figure 5(b) with smaller ![]() $\tau$,
$\tau$, ![]() $|\tilde {\eta }^{(1)}/\tilde {\eta }^{(0)}|$ becomes larger in wider regions, which means that the suppression occurs more strongly and extensively, although the suppression can be read only slightly from the solid circle at this temperature and cannot be read from the open circle closest to this temperature in figure 3. It is for
$|\tilde {\eta }^{(1)}/\tilde {\eta }^{(0)}|$ becomes larger in wider regions, which means that the suppression occurs more strongly and extensively, although the suppression can be read only slightly from the solid circle at this temperature and cannot be read from the open circle closest to this temperature in figure 3. It is for ![]() $\tau <3.2\times 10^{-3}$ in figure 3 that the suppression can be read explicitly from the experimental data (
$\tau <3.2\times 10^{-3}$ in figure 3 that the suppression can be read explicitly from the experimental data (![]() $\circ$); the suppression for
$\circ$); the suppression for ![]() $c=1$ and
$c=1$ and ![]() $U=\bar {U}$ should occur more strongly and extensively in this range of
$U=\bar {U}$ should occur more strongly and extensively in this range of ![]() $\tau$ than in figure 5(b). Thus, we overestimate the onset temperature of the suppression in the data of the self-diffusion coefficient if we evaluate the shear rate to be
$\tau$ than in figure 5(b). Thus, we overestimate the onset temperature of the suppression in the data of the self-diffusion coefficient if we evaluate the shear rate to be ![]() $\bar {U}/r_0$.
$\bar {U}/r_0$.
For ![]() $U=4\bar {U}$, as mentioned above, the maximum of
$U=4\bar {U}$, as mentioned above, the maximum of ![]() $\tau _{s^{(0)}}$ is
$\tau _{s^{(0)}}$ is ![]() $0.0264\times c^{0.518}$. The maximum is smaller than unity in the range of
$0.0264\times c^{0.518}$. The maximum is smaller than unity in the range of ![]() $c$ examined in figure 4, as supposed in our formulation. This also shows that our results are free from the details of a formal rule for large particle speed in appendix D. In the absence of the suppression, we have
$c$ examined in figure 4, as supposed in our formulation. This also shows that our results are free from the details of a formal rule for large particle speed in appendix D. In the absence of the suppression, we have ![]() $\xi =\xi _0\tau ^{-\nu }=28\ \textrm {nm}$ and
$\xi =\xi _0\tau ^{-\nu }=28\ \textrm {nm}$ and ![]() $120\ \textrm {nm}$ for
$120\ \textrm {nm}$ for ![]() $\tau =10^{-3}$ and
$\tau =10^{-3}$ and ![]() $10^{-4}$, respectively. The correlation length should be reduced by the strong shear, which suppresses the order-parameter fluctuation with small wavenumber. The correlation length under the shear effect is dependent on the direction, and proportional to
$10^{-4}$, respectively. The correlation length should be reduced by the strong shear, which suppresses the order-parameter fluctuation with small wavenumber. The correlation length under the shear effect is dependent on the direction, and proportional to ![]() $\tau ^{-0.5}$ at the largest in the stagnation-point flow (Onuki & Kawasaki Reference Onuki and Kawasaki1980c). This exponent is the same as in the mean-field approximation. The curvature of the stream line in figure 3 suggests that a typical length of the flow is several times larger than the particle diameter. Thus, a typical length of the flow is sufficiently large as compared with
$\tau ^{-0.5}$ at the largest in the stagnation-point flow (Onuki & Kawasaki Reference Onuki and Kawasaki1980c). This exponent is the same as in the mean-field approximation. The curvature of the stream line in figure 3 suggests that a typical length of the flow is several times larger than the particle diameter. Thus, a typical length of the flow is sufficiently large as compared with ![]() $\xi$ in the range of
$\xi$ in the range of ![]() $\tau$ examined in figure 3, as supposed in our formulation.
$\tau$ examined in figure 3, as supposed in our formulation.
It is assumed in (2.4) that the suppression is perfect if it occurs. In terms of the renormalization-group calculation, the singular part of the viscosity changes in the coarse-graining procedure, which makes sense until the resolution reaches ![]() $\xi$, and the way of the change is altered when the resolution exceeds a threshold determined by the shear rate. Equation (1.3) can be derived from the condition of whether the threshold comes before
$\xi$, and the way of the change is altered when the resolution exceeds a threshold determined by the shear rate. Equation (1.3) can be derived from the condition of whether the threshold comes before ![]() $\xi$ or not, as mentioned in the latter half of appendix A. In the procedure after the alteration, the singular part of the viscosity continues to be changed and becomes anisotropic. Thus, the assumption in (2.4) does not hold exactly. The ratio of the correction in the later stage, i.e. in the stage after the alteration, to the one in the earlier stage is evaluated by averaging the former correction over the directions in appendix E. If
$\xi$ or not, as mentioned in the latter half of appendix A. In the procedure after the alteration, the singular part of the viscosity continues to be changed and becomes anisotropic. Thus, the assumption in (2.4) does not hold exactly. The ratio of the correction in the later stage, i.e. in the stage after the alteration, to the one in the earlier stage is evaluated by averaging the former correction over the directions in appendix E. If ![]() $d=3$ is substituted into these results valid up to the linear order with respect to
$d=3$ is substituted into these results valid up to the linear order with respect to ![]() $4-d$, the evaluated ratio is smaller than
$4-d$, the evaluated ratio is smaller than ![]() $4\ (7)$ per cent for a pure-extension flow (a simple shear flow). These small values would support the appropriateness of (2.4), which can explain the data for the three-dimensional mixture of Beysens (Reference Beysens2019) in figure 3.
$4\ (7)$ per cent for a pure-extension flow (a simple shear flow). These small values would support the appropriateness of (2.4), which can explain the data for the three-dimensional mixture of Beysens (Reference Beysens2019) in figure 3.
In deriving (1.3), the lifetime of a correlated cluster and the range of the cluster size are evaluated. However, some deviations are possible in these evaluations, and may be required to compensate for the approximation in (2.4) mentioned above. For example, let us consider replacing ![]() $\xi$ with
$\xi$ with ![]() $1.5 \xi$ in (1.3). This replacement is equivalent with putting
$1.5 \xi$ in (1.3). This replacement is equivalent with putting ![]() $c$ equal to
$c$ equal to ![]() $1.5^{z}\approx 3.5$. A change of (1.3) to this extent cannot be denied from the data of Beysens (Reference Beysens2019) in figure 3, considering that the red short bars above the solid circles still lie in the middle of the distribution of the data.
$1.5^{z}\approx 3.5$. A change of (1.3) to this extent cannot be denied from the data of Beysens (Reference Beysens2019) in figure 3, considering that the red short bars above the solid circles still lie in the middle of the distribution of the data.
We simply link the drag coefficient with the self-diffusion coefficient by means of the one-dimensional Langevin equation for the particle velocity. Similar nonlinear Langevin equations are used for different problems in Klimontovich (Reference Klimontovich1994) and Lindner (Reference Lindner2007). Validity of the Langevin equation with the Stratonovich interpretation in our problem, where the viscosity can be inhomogeneous and dependent on the particle speed, remains to be founded on the fluctuating hydrodynamics, unlike in the cases studied by Bedeaux & Mazur (Reference Bedeaux and Mazur1974) and Mazur & van der Zwan (Reference Mazur and van der Zwan1978). It still appears that the Langevin equation can describe the data of Beysens (Reference Beysens2019) well in figure 3, where a rather large distribution of the data for small ![]() $\tau$ in the direction of the vertical axis may come from the properties of the viscosity in our problem.
$\tau$ in the direction of the vertical axis may come from the properties of the viscosity in our problem.
4. Summary and concluding remarks
Correlated clusters of the order-parameter fluctuation are generated in a near-critical binary fluid mixture lying in the homogeneous phase near the demixing critical point. The upper size of clusters, the correlation length, becomes larger as the critical point is approached. Then, as is well known, the convection of large and long-lived clusters enhances the transport coefficients in the coarse-grained dynamics (Kawasaki Reference Kawasaki1970). It is also well known that a sufficiently strong shear, if imposed, can deform long-lived clusters to suppress the critical enhancement (Onuki & Kawasaki Reference Onuki and Kawasaki1979). In a recent experiment (Beysens Reference Beysens2019), shear around a Brownian particle in a near-critical mixture on the critical isochore was suggested to cause this suppression to influence the motion. Deviation of the self-diffusion coefficient from the Stokes–Sutherland–Einstein formula was observed in the temperature range where the suppression is judged to occur from a typical shear rate around a particle moving with a typical speed.
How the deviation depends on the temperature is calculated in the present study. We first calculate the drag coefficient of a particle moving translationally in a mixture which is quiescent far from the particle. The suppression is simply assumed to occur perfectly when the cluster with the size of the correlation length becomes so long-lived as to be deformed by the shear. The shear rate is inhomogeneous and depends on the particle speed. Hence, the suppression makes the viscosity inhomogeneous and dependent on the particle speed. The calculation supposes a low Reynolds-number and a sufficiently weak influence of the shear on the viscosity, which are realized in the experiment. We next employ the drag coefficient thus calculated, dependent on the particle speed, as the frictional coefficient in a one-dimensional Langevin equation of the Stratonovich type to calculate the self-diffusion coefficient. The calculation results agree well with the experimental data, which is rather robust to changes in the threshold for the occurrence of the suppression.
Acknowledgements
The author thanks S. Yabunaka for helpful discussions.
Declaration of interests
The author reports no conflict of interest.
Appendix A. Previous results of the renormalization-group calculations
For an equilibrium binary fluid mixture in the homogeneous phase on the critical isochore near the critical point, as the renormalization steps are iterated, the Onsager coefficient for the interdiffusion approaches a constant, denoted by ![]() $\lambda ^*$. Rewinding the rescaling procedure to decrease the cutoff wavenumber
$\lambda ^*$. Rewinding the rescaling procedure to decrease the cutoff wavenumber ![]() $k$ at each iteration, we obtain the coefficient coarse grained up to
$k$ at each iteration, we obtain the coefficient coarse grained up to ![]() $k$. Writing
$k$. Writing ![]() $\lambda$ for it, we have
$\lambda$ for it, we have
that is, if ![]() $k\xi$ is larger than or comparable to unity. Here,
$k\xi$ is larger than or comparable to unity. Here, ![]() $k_{o}(\gg k)$ is the cutoff wavenumber before coarse graining and thus
$k_{o}(\gg k)$ is the cutoff wavenumber before coarse graining and thus ![]() $1/k_{o}$ has a microscopic length. If
$1/k_{o}$ has a microscopic length. If ![]() $k\xi$ is much smaller than unity,
$k\xi$ is much smaller than unity, ![]() $1/k$ in the parentheses of (A 1) should be replaced by
$1/k$ in the parentheses of (A 1) should be replaced by ![]() $\xi$; rewinding the rescaling procedure makes sense up to the length scale of
$\xi$; rewinding the rescaling procedure makes sense up to the length scale of ![]() $\xi$. Likewise, the singular part of
$\xi$. Likewise, the singular part of ![]() $\tilde {\eta }$ is given by
$\tilde {\eta }$ is given by ![]() $\tilde {\eta }^* (k_{o}/k)^{z-d}$ for
$\tilde {\eta }^* (k_{o}/k)^{z-d}$ for ![]() $\xi ^{-1} \stackrel {<}{\sim } k\ll k_{o}$ and
$\xi ^{-1} \stackrel {<}{\sim } k\ll k_{o}$ and
where ![]() $\tilde {\eta }^*$ denotes a constant for
$\tilde {\eta }^*$ denotes a constant for ![]() $\tilde {\eta }$ corresponding with
$\tilde {\eta }$ corresponding with ![]() $\lambda ^*$ (Onuki & Kawasaki Reference Onuki and Kawasaki1979). These exponents can be also derived from the dynamic scaling assumption (Folk & Moser Reference Folk and Moser2006).
$\lambda ^*$ (Onuki & Kawasaki Reference Onuki and Kawasaki1979). These exponents can be also derived from the dynamic scaling assumption (Folk & Moser Reference Folk and Moser2006).
We define the order parameter so that the coefficient of the square-gradient term in the dimensionless effective Hamiltonian is a half, as in Siggia et al. (Reference Siggia, Hohenberg and Halperin1976), Onuki & Kawasaki (Reference Onuki and Kawasaki1979) and Onuki (Reference Onuki2002). In the Fourier transform mentioned above (1.1), we put the two times equal to each other and write ![]() $\chi _k$ for the result, which is the static correlation function or static susceptibility. We have
$\chi _k$ for the result, which is the static correlation function or static susceptibility. We have ![]() $\chi _k\approx \xi ^2(k/k_{o})^{\eta }$ for
$\chi _k\approx \xi ^2(k/k_{o})^{\eta }$ for ![]() $k\xi \ll 1$. As
$k\xi \ll 1$. As ![]() $k\to 0$ and
$k\to 0$ and ![]() $\xi \to \infty$ with
$\xi \to \infty$ with ![]() $k\xi$ being an arbitrary positive number, the renormalization-group calculation gives (Siggia et al. Reference Siggia, Hohenberg and Halperin1976)
$k\xi$ being an arbitrary positive number, the renormalization-group calculation gives (Siggia et al. Reference Siggia, Hohenberg and Halperin1976)
where the Kawasaki amplitude ![]() $R$ is a universal constant approximately equal to
$R$ is a universal constant approximately equal to ![]() $1/(6{\rm \pi} )$. The dimensionless scaling function,
$1/(6{\rm \pi} )$. The dimensionless scaling function, ![]() ${\bar \varOmega }$, tends to unity as its variable approaches zero. Considering that
${\bar \varOmega }$, tends to unity as its variable approaches zero. Considering that ![]() $\lambda \tilde {\eta } \xi ^{d-2}$ divided by
$\lambda \tilde {\eta } \xi ^{d-2}$ divided by ![]() $\chi _k$ equals
$\chi _k$ equals ![]() $Rk_{B}T_{c}$ for
$Rk_{B}T_{c}$ for ![]() $k\xi \ll 1$, we have
$k\xi \ll 1$, we have
with ![]() $k\xi$ being fixed to be small (Siggia et al. Reference Siggia, Hohenberg and Halperin1976).
$k\xi$ being fixed to be small (Siggia et al. Reference Siggia, Hohenberg and Halperin1976).
According to the renormalization-group calculation up to the order of ![]() $\epsilon \equiv 4-d$ in the presence of a simple shear flow (Onuki & Kawasaki Reference Onuki and Kawasaki1979), (A 1) is found to break down for
$\epsilon \equiv 4-d$ in the presence of a simple shear flow (Onuki & Kawasaki Reference Onuki and Kawasaki1979), (A 1) is found to break down for ![]() $k\stackrel {<}{\sim }k_s$, where
$k\stackrel {<}{\sim }k_s$, where ![]() $k_s$ is defined so that
$k_s$ is defined so that
holds. The shear is strong enough to suppress the critical enhancement if ![]() $k_s\xi \gtrsim 1$ holds;
$k_s\xi \gtrsim 1$ holds; ![]() $k_s$ then comes before
$k_s$ then comes before ![]() $1/\xi$ in the coarse-graining process of decreasing
$1/\xi$ in the coarse-graining process of decreasing ![]() $k$ (figure 6). Otherwise,
$k$ (figure 6). Otherwise, ![]() $\lambda$ for
$\lambda$ for ![]() $k\xi \ll 1$ remains given by (A 1) with
$k\xi \ll 1$ remains given by (A 1) with ![]() $1/k$ being replaced by
$1/k$ being replaced by ![]() $\xi$. With the aid of (A 3)–(A 5), we find that this condition of strong shear approximately agrees with (1.3). From (2.3) and (A 5), we have
$\xi$. With the aid of (A 3)–(A 5), we find that this condition of strong shear approximately agrees with (1.3). From (2.3) and (A 5), we have ![]() $k_s^{-1}=\xi _0 \tau _s^{-\nu }$ and
$k_s^{-1}=\xi _0 \tau _s^{-\nu }$ and
Ambiguity on the condition of strong shear is discussed in § 3.

Figure 6. A schematic graph showing how ![]() $\lambda$ changes as the mixture is coarse grained, which is made from figure 2 of Onuki & Kawasaki (Reference Onuki and Kawasaki1979). We define
$\lambda$ changes as the mixture is coarse grained, which is made from figure 2 of Onuki & Kawasaki (Reference Onuki and Kawasaki1979). We define ![]() $k$ so that the cutoff wavenumber viewed on the original lattice equals
$k$ so that the cutoff wavenumber viewed on the original lattice equals ![]() $k$ at the iteration number,
$k$ at the iteration number, ![]() $l$, in the renormalization-group calculation. We have
$l$, in the renormalization-group calculation. We have ![]() $k/k_{o}=\tilde{b}^{-l}$, where
$k/k_{o}=\tilde{b}^{-l}$, where ![]() $\tilde{b}$ is the length rescaling factor. The curve follows (A 1) for
$\tilde{b}$ is the length rescaling factor. The curve follows (A 1) for ![]() $k_{o}\gg k \gg k_s$, but deviates from (A 1) for
$k_{o}\gg k \gg k_s$, but deviates from (A 1) for ![]() $k_s\gtrsim k$.
$k_s\gtrsim k$.
The above-mentioned breakdown of (A 1) occurs when the static susceptibility deviates from the Ornstein–Zernike form in the mean-field approximation for an equilibrium fluid mixture. Then, using the wavenumber vector ![]() $\boldsymbol {k}$, we should write
$\boldsymbol {k}$, we should write ![]() $\chi _{\boldsymbol {k}}$, not
$\chi _{\boldsymbol {k}}$, not ![]() $\chi _k$, for the susceptibility because of its anisotropy. The method of characteristics is used to calculate
$\chi _k$, for the susceptibility because of its anisotropy. The method of characteristics is used to calculate ![]() $\chi _{\boldsymbol {k}}$ for a simple shear flow in § 3 of Onuki & Kawasaki (Reference Onuki and Kawasaki1979), and for other kinds of linear shear flow in § 4 of Onuki & Kawasaki (Reference Onuki and Kawasaki1980a) and § 3 of Onuki & Kawasaki (Reference Onuki and Kawasaki1980c). In this method, a wavenumber vector dependent on a parameter, with the dimension of the time, is introduced, and the ‘time’ derivative of the vector equals the product of the matrix of the velocity gradient and the vector. Thus,
$\chi _{\boldsymbol {k}}$ for a simple shear flow in § 3 of Onuki & Kawasaki (Reference Onuki and Kawasaki1979), and for other kinds of linear shear flow in § 4 of Onuki & Kawasaki (Reference Onuki and Kawasaki1980a) and § 3 of Onuki & Kawasaki (Reference Onuki and Kawasaki1980c). In this method, a wavenumber vector dependent on a parameter, with the dimension of the time, is introduced, and the ‘time’ derivative of the vector equals the product of the matrix of the velocity gradient and the vector. Thus, ![]() $s$ in (1.3) can be determined in the way described in § 1.
$s$ in (1.3) can be determined in the way described in § 1.
The renormalization correction of ![]() $\lambda$ in the later stage with
$\lambda$ in the later stage with ![]() $k<k_s$ in a simple shear flow becomes dependent not only on
$k<k_s$ in a simple shear flow becomes dependent not only on ![]() $k$ but also on
$k$ but also on ![]() $\boldsymbol {k}$, and is much smaller than the one in the earlier stage with
$\boldsymbol {k}$, and is much smaller than the one in the earlier stage with ![]() $k>k_s$ even when
$k>k_s$ even when ![]() $\epsilon$ is put equal to unity, as shown by (4.62) and (4.85) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979). We draw figure 6 from figure 2 of Onuki & Kawasaki (Reference Onuki and Kawasaki1979), where it is stated that the singular part of the viscosity behaves in the same fashion, although the viscosity for
$\epsilon$ is put equal to unity, as shown by (4.62) and (4.85) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979). We draw figure 6 from figure 2 of Onuki & Kawasaki (Reference Onuki and Kawasaki1979), where it is stated that the singular part of the viscosity behaves in the same fashion, although the viscosity for ![]() $k<k_s$ is not only dependent on
$k<k_s$ is not only dependent on ![]() $\boldsymbol {k}$ but also expressed in terms of an anisotropic tensor (Onuki & Kawasaki Reference Onuki and Kawasaki1980b). Within a simplified picture of figure 6, assuming (2.4) amounts to drawing the curve of the singular part of
$\boldsymbol {k}$ but also expressed in terms of an anisotropic tensor (Onuki & Kawasaki Reference Onuki and Kawasaki1980b). Within a simplified picture of figure 6, assuming (2.4) amounts to drawing the curve of the singular part of ![]() $\tilde {\eta }$ as if the curve for
$\tilde {\eta }$ as if the curve for ![]() $k\ge k_s$ were perfectly free from the shear effect and linked to a horizontal line in
$k\ge k_s$ were perfectly free from the shear effect and linked to a horizontal line in ![]() $k<k_s$.
$k<k_s$.
Appendix B. Local shear rate
We here examine how ![]() $\boldsymbol {\nabla } \boldsymbol {v}^{(0)}$ changes around a particle, which is briefly mentioned above (2.14). From (2.8a–c), we can calculate the components of
$\boldsymbol {\nabla } \boldsymbol {v}^{(0)}$ changes around a particle, which is briefly mentioned above (2.14). From (2.8a–c), we can calculate the components of ![]() $\boldsymbol {\nabla } \boldsymbol {v}^{(0)}$ with respect to the three-dimensional Cartesian coordinates
$\boldsymbol {\nabla } \boldsymbol {v}^{(0)}$ with respect to the three-dimensional Cartesian coordinates ![]() $(x,y,z)$ at a point on the
$(x,y,z)$ at a point on the ![]() $xz$ plane (
$xz$ plane (![]() $\phi =0$). There, the
$\phi =0$). There, the ![]() $(x,y)$,
$(x,y)$, ![]() $(y,x)$,
$(y,x)$, ![]() $(y,z)$ and
$(y,z)$ and ![]() $(z,y)$ components vanish. The components can be expressed in terms of a
$(z,y)$ components vanish. The components can be expressed in terms of a ![]() $3\times 3$ matrix. We rewrite this matrix as the sum of two matrices; one is the diagonal matrix with the diagonal elements being
$3\times 3$ matrix. We rewrite this matrix as the sum of two matrices; one is the diagonal matrix with the diagonal elements being
from the top. We rotate the ![]() $(x,z)$ coordinates to have
$(x,z)$ coordinates to have ![]() $(x',z')$ coordinates so that the diagonal elements of the other matrix of the two vanish at the point; the diagonal matrix mentioned above is not changed by this rotation. The components of the velocity gradient with respect to the coordinates
$(x',z')$ coordinates so that the diagonal elements of the other matrix of the two vanish at the point; the diagonal matrix mentioned above is not changed by this rotation. The components of the velocity gradient with respect to the coordinates ![]() $(x', y, z')$ are given by
$(x', y, z')$ are given by
 \begin{equation} \frac{U}{r_0} \left[\begin{pmatrix} -C/2 & 0 & 0 \\ 0 & C & 0 \\ 0 & 0 & -C/2 \end{pmatrix}+\begin{pmatrix} 0 & 0 & B-A \\ 0 & 0 & 0 \\ B+A & 0 & 0 \end{pmatrix}\right], \end{equation}
\begin{equation} \frac{U}{r_0} \left[\begin{pmatrix} -C/2 & 0 & 0 \\ 0 & C & 0 \\ 0 & 0 & -C/2 \end{pmatrix}+\begin{pmatrix} 0 & 0 & B-A \\ 0 & 0 & 0 \\ B+A & 0 & 0 \end{pmatrix}\right], \end{equation}
where we use ![]() $A\equiv 3\sin {\theta }/(4\rho ^2)$. We define
$A\equiv 3\sin {\theta }/(4\rho ^2)$. We define ![]() $C$ as
$C$ as ![]() $\nabla _yv^{(0)}_y= 3(\rho ^2-1)\cos {\theta }/(4\rho ^4)$, and define
$\nabla _yv^{(0)}_y= 3(\rho ^2-1)\cos {\theta }/(4\rho ^4)$, and define ![]() $B$ as
$B$ as ![]() $3/(8\rho ^4)$ multiplied by the square root of
$3/(8\rho ^4)$ multiplied by the square root of
Thus, ![]() $A$ and
$A$ and ![]() $B$ are non-negative. The first term in the square brackets of (B 2) represents a pure-extension flow.
$B$ are non-negative. The first term in the square brackets of (B 2) represents a pure-extension flow.
We define ![]() $\varOmega _{e}$ as
$\varOmega _{e}$ as ![]() $\sqrt {B^2-A^2}$, and have
$\sqrt {B^2-A^2}$, and have
which vanishes at ![]() $\rho =1$. As mentioned in the fourth paragraph of § 1, the exponential of the product of (B 2) and the time
$\rho =1$. As mentioned in the fourth paragraph of § 1, the exponential of the product of (B 2) and the time ![]() $t$ works as the time evolution operator for a convected line segment. The long-wavelength fluctuations of the order parameter are suppressed in the stretching direction. The exponential equals
$t$ works as the time evolution operator for a convected line segment. The long-wavelength fluctuations of the order parameter are suppressed in the stretching direction. The exponential equals
 \begin{equation} \begin{pmatrix} e^{-C\check{t}/2} \textrm{cosh}\varOmega_{e}\check{t} & 0 & \left(B-A\right) \varOmega_{e}^{-1} e^{-C\check{t}/2} \textrm{sinh}\varOmega_{e}\check{t}\\ 0 & e^{C\check{t}} & 0 \\ \left(B+A\right) \varOmega_{e}^{-1} e^{-C\check{t}/2} \textrm{sinh}\varOmega_{e}\check{t} & 0 & e^{-C\check{t}/2} \textrm{cosh}\varOmega_{e}\check{t}, \end{pmatrix}\end{equation}
\begin{equation} \begin{pmatrix} e^{-C\check{t}/2} \textrm{cosh}\varOmega_{e}\check{t} & 0 & \left(B-A\right) \varOmega_{e}^{-1} e^{-C\check{t}/2} \textrm{sinh}\varOmega_{e}\check{t}\\ 0 & e^{C\check{t}} & 0 \\ \left(B+A\right) \varOmega_{e}^{-1} e^{-C\check{t}/2} \textrm{sinh}\varOmega_{e}\check{t} & 0 & e^{-C\check{t}/2} \textrm{cosh}\varOmega_{e}\check{t}, \end{pmatrix}\end{equation}
where we use ![]() $\check {t}\equiv t U/r_0$ and note that the matrices in the square brackets of (B 2) commute. In figure 7 with
$\check {t}\equiv t U/r_0$ and note that the matrices in the square brackets of (B 2) commute. In figure 7 with ![]() $\rho =1.5$, we have
$\rho =1.5$, we have ![]() $A>B$, i.e. purely imaginary
$A>B$, i.e. purely imaginary ![]() $\varOmega _{e}$, for
$\varOmega _{e}$, for ![]() $0.74<\theta <2.4$ approximately, and
$0.74<\theta <2.4$ approximately, and ![]() $C^2>\varOmega _{e}^2$ for
$C^2>\varOmega _{e}^2$ for ![]() $0.6 <\theta <2.5$ approximately. Although data are not shown, as
$0.6 <\theta <2.5$ approximately. Although data are not shown, as ![]() $\rho$ increases above unity, the
$\rho$ increases above unity, the ![]() $\theta$ region with
$\theta$ region with ![]() $A>B$ and the one with
$A>B$ and the one with ![]() $C^2>\varOmega _{e}^2$ are narrower. We find that
$C^2>\varOmega _{e}^2$ are narrower. We find that ![]() $A>B$ holds at
$A>B$ holds at ![]() $\theta ={\rm \pi} /2$ for any
$\theta ={\rm \pi} /2$ for any ![]() $\rho$ larger than unity and that
$\rho$ larger than unity and that ![]() $\varOmega _{e}=1.5|C|$ holds at
$\varOmega _{e}=1.5|C|$ holds at ![]() $\theta =0$ and
$\theta =0$ and ![]() ${\rm \pi}$. As
${\rm \pi}$. As ![]() $\theta$ changes from
$\theta$ changes from ![]() $0$ or
$0$ or ![]() ${\rm \pi}$ to
${\rm \pi}$ to ![]() ${\rm \pi} /2$,
${\rm \pi} /2$, ![]() $\varOmega _{e}^2$ decreases more rapidly than
$\varOmega _{e}^2$ decreases more rapidly than ![]() $C^2$, as shown in figure 7. The two-dimensional flow with
$C^2$, as shown in figure 7. The two-dimensional flow with ![]() $C=0$ is considered in Onuki & Kawasaki (Reference Onuki and Kawasaki1980c), where a rotational flow with
$C=0$ is considered in Onuki & Kawasaki (Reference Onuki and Kawasaki1980c), where a rotational flow with ![]() $A>B$ is shown to be weak in suppressing the critical enhancement. For simplicity, we thus neglect the periodic deformation of a cluster in determining the local shear rate.
$A>B$ is shown to be weak in suppressing the critical enhancement. For simplicity, we thus neglect the periodic deformation of a cluster in determining the local shear rate.

Figure 7. We plot ![]() $\varOmega _{e}^2$ (solid curve) and
$\varOmega _{e}^2$ (solid curve) and ![]() $C^2$ (dashed curve) at
$C^2$ (dashed curve) at ![]() $\rho =1.5$ against
$\rho =1.5$ against ![]() $\theta$.
$\theta$.
We suppose ![]() $U>0$ in this paragraph. In the components of (B 5), when
$U>0$ in this paragraph. In the components of (B 5), when ![]() $\varOmega _{e}$ is real, the largest stretching rate is
$\varOmega _{e}$ is real, the largest stretching rate is ![]() $CU/r_0$ if
$CU/r_0$ if ![]() $C>0$ and is
$C>0$ and is ![]() $(2\varOmega _{e}-C)U/(2r_0)$ if
$(2\varOmega _{e}-C)U/(2r_0)$ if ![]() $C<0$. When
$C<0$. When ![]() $\varOmega _{e}$ is imaginary, the largest stretching rate is
$\varOmega _{e}$ is imaginary, the largest stretching rate is ![]() $CU/r_0$ if
$CU/r_0$ if ![]() $C>0$ and is
$C>0$ and is ![]() $-CU/(2r_0)$ if
$-CU/(2r_0)$ if ![]() $C<0$. These results agree with (2.14), considering that (2.14) with
$C<0$. These results agree with (2.14), considering that (2.14) with ![]() $c=1$ equals
$c=1$ equals ![]() $|C{U}|{/r_0}$. We find for
$|C{U}|{/r_0}$. We find for ![]() $U>0$ that
$U>0$ that ![]() $c$ is unity for
$c$ is unity for ![]() $0\le \theta \le {\rm \pi}/2$, is
$0\le \theta \le {\rm \pi}/2$, is ![]() $1/2$ for
$1/2$ for ![]() ${\rm \pi} /2< \theta \le {\rm \pi}$ and
${\rm \pi} /2< \theta \le {\rm \pi}$ and ![]() $\varOmega _{e}^2<0$, and increases up to
$\varOmega _{e}^2<0$, and increases up to ![]() $2$ as
$2$ as ![]() $\theta$ increases in the region of
$\theta$ increases in the region of ![]() ${\rm \pi} /2< \theta \le {\rm \pi}$ and
${\rm \pi} /2< \theta \le {\rm \pi}$ and ![]() $\varOmega _{e}^2\ge 0$.
$\varOmega _{e}^2\ge 0$.
Appendix C. Some details in calculating the drag force
We introduce
and the kernel appearing in (2.22) is given by
together with ![]() $\varGamma _J(\rho ,\sigma )=\varGamma _J(\sigma ,\rho )$ for
$\varGamma _J(\rho ,\sigma )=\varGamma _J(\sigma ,\rho )$ for ![]() $\rho <\sigma$. The kernel above for
$\rho <\sigma$. The kernel above for ![]() $J=1$ is equal to
$J=1$ is equal to ![]() $1/30$ multiplied by
$1/30$ multiplied by ![]() $\varGamma _{R}$ of Okamoto et al. (Reference Okamoto, Fujitani and Komura2013). Similar calculations are there in Fujitani (Reference Fujitani2018) and Yabunaka & Fujitani (Reference Yabunaka and Fujitani2020).
$\varGamma _{R}$ of Okamoto et al. (Reference Okamoto, Fujitani and Komura2013). Similar calculations are there in Fujitani (Reference Fujitani2018) and Yabunaka & Fujitani (Reference Yabunaka and Fujitani2020).
As mentioned above (2.23), we can delete ![]() $\varPi _J$ and
$\varPi _J$ and ![]() $T_J$ from the last two terms of (2.13). A similar procedure can be found in deriving (4.19) of Okamoto et al. (Reference Okamoto, Fujitani and Komura2013). By using
$T_J$ from the last two terms of (2.13). A similar procedure can be found in deriving (4.19) of Okamoto et al. (Reference Okamoto, Fujitani and Komura2013). By using
where ![]() $\delta _{ij}$ implies the Kronecker delta, we find the surface integral of the last two term of (2.13) to be given by
$\delta _{ij}$ implies the Kronecker delta, we find the surface integral of the last two term of (2.13) to be given by
Differentiating (2.5) with respect to ![]() $\rho$ or
$\rho$ or ![]() $\theta$ yields a term having the derivative of the step function, i.e. the delta function. Noting that this term vanishes because of its prefactor, we find that the negative of the right-hand side of (2.12) can be rewritten as
$\theta$ yields a term having the derivative of the step function, i.e. the delta function. Noting that this term vanishes because of its prefactor, we find that the negative of the right-hand side of (2.12) can be rewritten as
Here, the vector ![]() $\boldsymbol {h}$ dependent on
$\boldsymbol {h}$ dependent on ![]() $(\rho ,\theta )$ can be calculated by using (2.8a–c). Because (2.17) is equal to (C 5), we use the orthogonality of the vector spherical harmonics to calculate
$(\rho ,\theta )$ can be calculated by using (2.8a–c). Because (2.17) is equal to (C 5), we use the orthogonality of the vector spherical harmonics to calculate ![]() $F_1$ and
$F_1$ and ![]() $H_1$. For example,
$H_1$. For example, ![]() $H_1(\rho )$ is the integral of the inner product of vectors of (C 5) and
$H_1(\rho )$ is the integral of the inner product of vectors of (C 5) and ![]() $\boldsymbol {B}_{10}$ over the surface of the unit sphere. We thus find that
$\boldsymbol {B}_{10}$ over the surface of the unit sphere. We thus find that ![]() $H_1(\rho )$ vanishes at
$H_1(\rho )$ vanishes at ![]() $\rho =1$, where (2.14), and thus
$\rho =1$, where (2.14), and thus ![]() $\check {\tau }_{s^{(0)}}$ vanish.
$\check {\tau }_{s^{(0)}}$ vanish.
Substituting (2.8a–c) into the right-hand side of (2.12) and defining ![]() $\zeta$ as
$\zeta$ as ![]() $(d/z)-1$, we find that the components of
$(d/z)-1$, we find that the components of ![]() $\boldsymbol {h}$ are given by
$\boldsymbol {h}$ are given by
 \begin{equation} \left. \begin{gathered} h_r(\rho,\theta)=\left\{ \frac{1-\check{\tau}_s^{\nu(d-z)}}{\rho^3}+\zeta \check{\tau}^{\nu(d-z)} \left[ \frac{1-\rho^2}{\rho^4 s}\frac{\partial s}{\partial \rho}+\frac{1}{2\rho^5 s} \frac{\partial s}{\partial\theta}\tan{\theta}\right]\right\} \cos{\theta},\\ h_{\theta}(\rho,\theta)=\left\{ \frac{1-\check{\tau}_s^{\nu(d-z)}}{2\rho^3} +\zeta \check{\tau}^{\nu(d-z)}\left[ \frac{1}{2\rho^4 s}\frac{\partial s}{\partial \rho}+\frac{\rho^2-1}{2\rho^5 s} \frac{\partial s}{\partial\theta}{\cot}{\theta}\right]\right\}\sin{\theta}, \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} h_r(\rho,\theta)=\left\{ \frac{1-\check{\tau}_s^{\nu(d-z)}}{\rho^3}+\zeta \check{\tau}^{\nu(d-z)} \left[ \frac{1-\rho^2}{\rho^4 s}\frac{\partial s}{\partial \rho}+\frac{1}{2\rho^5 s} \frac{\partial s}{\partial\theta}\tan{\theta}\right]\right\} \cos{\theta},\\ h_{\theta}(\rho,\theta)=\left\{ \frac{1-\check{\tau}_s^{\nu(d-z)}}{2\rho^3} +\zeta \check{\tau}^{\nu(d-z)}\left[ \frac{1}{2\rho^4 s}\frac{\partial s}{\partial \rho}+\frac{\rho^2-1}{2\rho^5 s} \frac{\partial s}{\partial\theta}{\cot}{\theta}\right]\right\}\sin{\theta}, \end{gathered} \right\} \end{equation}
and ![]() $h_{\phi }=0$, where we write
$h_{\phi }=0$, where we write ![]() $s$ for
$s$ for ![]() $s^{(0)}$ for conciseness. We have
$s^{(0)}$ for conciseness. We have ![]() $h_r(\rho ,\theta )=-h_r(\rho ,{\rm \pi} -\theta )$ and
$h_r(\rho ,\theta )=-h_r(\rho ,{\rm \pi} -\theta )$ and ![]() $h_{\theta }(\rho ,\theta )= h_{\theta }(\rho ,{\rm \pi} -\theta )$. From (2.20) for
$h_{\theta }(\rho ,\theta )= h_{\theta }(\rho ,{\rm \pi} -\theta )$. From (2.20) for ![]() $J=1$, we obtain
$J=1$, we obtain
where ![]() $\partial _{\rho }$ operates on all the following terms including the step function.
$\partial _{\rho }$ operates on all the following terms including the step function.
Substituting (C 7) into (2.24), we employ integration by parts with respect to ![]() $\rho$, and the resultant integrand contains the step function, not its derivative. Writing
$\rho$, and the resultant integrand contains the step function, not its derivative. Writing ![]() $\check {U}_c$ for
$\check {U}_c$ for ![]() ${c}|U|/U^*$, we have
${c}|U|/U^*$, we have
 \begin{equation} \check{\tau}_{s^{(0)}}(\rho, \theta)=\frac{1}{\tau} \left[\frac{3\left(\rho^2-1\right)}{4\rho^4} \check{U}_c\cos{\theta}\right]^{1/(\nu z)} \end{equation}
\begin{equation} \check{\tau}_{s^{(0)}}(\rho, \theta)=\frac{1}{\tau} \left[\frac{3\left(\rho^2-1\right)}{4\rho^4} \check{U}_c\cos{\theta}\right]^{1/(\nu z)} \end{equation}in (C 7). Thus, the step function in (C 7) can be non-zero if
whose left-hand side is quadratic with respect to ![]() $\rho ^2$. Putting the left-hand side above equal to zero gives
$\rho ^2$. Putting the left-hand side above equal to zero gives ![]() $\rho =\rho _{\pm }$ and
$\rho =\rho _{\pm }$ and ![]() $\rho =-\rho _{\pm }$, where
$\rho =-\rho _{\pm }$, where ![]() $\rho _{\pm }$ is defined as
$\rho _{\pm }$ is defined as
 \begin{equation} \rho_{\pm}(\theta)\equiv \left(\frac{3\check{U}_c}{8\tau^{\nu z}}\cos{\theta}\pm\frac{\sqrt{\varDelta(\theta)}}{2}\right)^{1/2}. \end{equation}
\begin{equation} \rho_{\pm}(\theta)\equiv \left(\frac{3\check{U}_c}{8\tau^{\nu z}}\cos{\theta}\pm\frac{\sqrt{\varDelta(\theta)}}{2}\right)^{1/2}. \end{equation}
Here, ![]() $\varDelta$ is the discriminant, given by
$\varDelta$ is the discriminant, given by
Equation (2.24) does not vanish if ![]() $\varDelta$ is positive and if
$\varDelta$ is positive and if ![]() $\rho _-<\rho <\rho _+$, where we have
$\rho _-<\rho <\rho _+$, where we have ![]() $1<\rho _-<\rho _+$ for
$1<\rho _-<\rho _+$ for ![]() $\varDelta >0$.
$\varDelta >0$.
We introduce
 \begin{equation} G_{m,n}(\theta)\equiv \varTheta(\varDelta(\theta))\int_{\rho_-(\theta)}^{\rho_+(\theta)}\,\textrm{d}\rho \left(\frac{\rho^2-1}{\rho^4}\right)^{\zeta-m} \frac{1}{\rho^n}, \end{equation}
\begin{equation} G_{m,n}(\theta)\equiv \varTheta(\varDelta(\theta))\int_{\rho_-(\theta)}^{\rho_+(\theta)}\,\textrm{d}\rho \left(\frac{\rho^2-1}{\rho^4}\right)^{\zeta-m} \frac{1}{\rho^n}, \end{equation}
which is expressed in terms of Gauss’ hypergeometric function according to Mathematica (Wolfram Research). The integral of (2.24) is found to be the sum of the integrals of the following three integrands over ![]() $0<\theta <{\rm \pi} /2$. The integrands are
$0<\theta <{\rm \pi} /2$. The integrands are
 \begin{equation} \varTheta(\varDelta(\theta))\int_{\rho_-(\theta)}^{\rho_+(\theta)}\,\textrm{d}\rho\ \left(\frac{3\rho^2+1}{4\rho^4}\sin^3{\theta}+\frac{1-3\rho^2}{\rho^4}\sin{\theta}\cos^2{\theta}\right), \end{equation}
\begin{equation} \varTheta(\varDelta(\theta))\int_{\rho_-(\theta)}^{\rho_+(\theta)}\,\textrm{d}\rho\ \left(\frac{3\rho^2+1}{4\rho^4}\sin^3{\theta}+\frac{1-3\rho^2}{\rho^4}\sin{\theta}\cos^2{\theta}\right), \end{equation}
where the integration with respect to ![]() $\rho$ is elementary,
$\rho$ is elementary,
 \begin{equation} -\left(\frac{3\check{U}_c}{4\tau^{\nu z}}\right)^{\zeta} \frac{1}{4}\left[3G_{0, 2}+G_{0, 4}+\zeta\left(3 G_{1,4}-5 G_{1,6}-G_{1,8}-5G_{1,10}\right)\right] \cos^{\zeta}{\theta}\sin^3{\theta} \end{equation}
\begin{equation} -\left(\frac{3\check{U}_c}{4\tau^{\nu z}}\right)^{\zeta} \frac{1}{4}\left[3G_{0, 2}+G_{0, 4}+\zeta\left(3 G_{1,4}-5 G_{1,6}-G_{1,8}-5G_{1,10}\right)\right] \cos^{\zeta}{\theta}\sin^3{\theta} \end{equation}and
 \begin{equation} \left(\frac{3\check{U}_c}{4\tau^{\nu z}}\right)^{\zeta} \left[3G_{0,2}-G_{0,4}-\zeta\left( 6G_{0,2}-14G_{0,4}+4G_{0,6}\right)\right] \cos^{\zeta+2}{\theta}\sin{\theta}, \end{equation}
\begin{equation} \left(\frac{3\check{U}_c}{4\tau^{\nu z}}\right)^{\zeta} \left[3G_{0,2}-G_{0,4}-\zeta\left( 6G_{0,2}-14G_{0,4}+4G_{0,6}\right)\right] \cos^{\zeta+2}{\theta}\sin{\theta}, \end{equation}
where the variable ![]() $\theta$ of
$\theta$ of ![]() $G_{m, n}$ is dropped for conciseness.
$G_{m, n}$ is dropped for conciseness.
Appendix D. Self-diffusion coefficient
The Fokker–Planck equation corresponding to (2.26) is
where ![]() $P(U,t;U_0)$ represents the probability density of
$P(U,t;U_0)$ represents the probability density of ![]() $U$ at a time
$U$ at a time ![]() $t$ on condition that
$t$ on condition that ![]() $U=U_0$ at
$U=U_0$ at ![]() $t=0$. The variables of the functions are dropped on the right-hand side above for conciseness. The stationary solution, denoted by
$t=0$. The variables of the functions are dropped on the right-hand side above for conciseness. The stationary solution, denoted by ![]() $P_{eq}(U)$, is proportional to (Risken Reference Risken2002)
$P_{eq}(U)$, is proportional to (Risken Reference Risken2002)
which should be proportional to the Boltzmann distribution (Zwanzig & Bixon Reference Zwanzig and Bixon1975),
Considering that ![]() $b^2$ equals
$b^2$ equals ![]() $2\gamma k_{B}T$ if
$2\gamma k_{B}T$ if ![]() $\gamma (U)$ is independent of
$\gamma (U)$ is independent of ![]() $U$, we find
$U$, we find
We can rewrite the right-hand side above by changing the integration interval to the one from ![]() $U$ to
$U$ to ![]() $-\infty$ because the integral from
$-\infty$ because the integral from ![]() $-\infty$ to
$-\infty$ to ![]() $\infty$ vanishes. Then, using integration by parts, we find that
$\infty$ vanishes. Then, using integration by parts, we find that ![]() $|b(U)^2-2k_{B}T \gamma (U)|$ equals
$|b(U)^2-2k_{B}T \gamma (U)|$ equals
where the prime indicates the derivative. We can assume that ![]() $\check {\gamma }(u)$ decreases to a positive constant as
$\check {\gamma }(u)$ decreases to a positive constant as ![]() $|u|$ increases to
$|u|$ increases to ![]() $\infty$ for the reason mentioned in the next paragraph. Thus, for
$\infty$ for the reason mentioned in the next paragraph. Thus, for ![]() $U<0$, (D 5) becomes larger if we replace
$U<0$, (D 5) becomes larger if we replace ![]() $\gamma '(U_1)$ with a suitable positive constant. Using an asymptotic form of a complementary error function, we find that (D 5) vanishes, and thus
$\gamma '(U_1)$ with a suitable positive constant. Using an asymptotic form of a complementary error function, we find that (D 5) vanishes, and thus ![]() $b(U)^2$ remains finite, in the limit of
$b(U)^2$ remains finite, in the limit of ![]() $U\to -\infty$. This result is used later.
$U\to -\infty$. This result is used later.
We can make a convenient formal rule for the particle speed larger than assumed in the text, because we later find its influence on (2.28) negligible. In other words, making such a rule is a substitute for introducing an upper cutoff of the particle speed to the model in the text. For definiteness, we here specify a formal rule. In (2.1), we should replace ![]() $\tau$ with unity for
$\tau$ with unity for ![]() $\tau >1$. Accordingly, (2.4) is supplemented with the rule
$\tau >1$. Accordingly, (2.4) is supplemented with the rule ![]() $\tilde {\eta }=\tilde {\eta }_{B}(T)$ for
$\tilde {\eta }=\tilde {\eta }_{B}(T)$ for ![]() $\tau >1$ if
$\tau >1$ if ![]() $\tau _s<1$ and for any
$\tau _s<1$ and for any ![]() $\tau$ otherwise. As the particle speed is larger, because the region with
$\tau$ otherwise. As the particle speed is larger, because the region with ![]() $\tau _s>1$ approaches the whole mixture region,
$\tau _s>1$ approaches the whole mixture region, ![]() ${\gamma }(U)$ approaches Stokes’ law of
${\gamma }(U)$ approaches Stokes’ law of ![]() $6{\rm \pi} \tilde {\eta }_{B}(T) r_0$ from the larger side. This means that
$6{\rm \pi} \tilde {\eta }_{B}(T) r_0$ from the larger side. This means that ![]() $\check {\gamma }(\infty )$ is not smaller than
$\check {\gamma }(\infty )$ is not smaller than ![]() $\tau ^{\nu (z-d)}$, which is
$\tau ^{\nu (z-d)}$, which is ![]() $0.75$ and
$0.75$ and ![]() $0.68$ for
$0.68$ for ![]() $\tau =10^{-3}$ and
$\tau =10^{-3}$ and ![]() $10^{-4}$, respectively. Thus, the assumption mentioned in the preceding paragraph holds in the range of
$10^{-4}$, respectively. Thus, the assumption mentioned in the preceding paragraph holds in the range of ![]() $\tau$ of figure 3.
$\tau$ of figure 3.
Introducing a Laplace transform, defined as
we use ![]() $\langle U_0 \rangle =0$ to rewrite (2.27) as
$\langle U_0 \rangle =0$ to rewrite (2.27) as
From the Laplace transform of (D 1), we use (D 2) and (D 3) to obtain
where ![]() $\delta$ represents the delta function. With
$\delta$ represents the delta function. With ![]() $\mathcal {O}$ indicating the Landau symbol, we have
$\mathcal {O}$ indicating the Landau symbol, we have ![]() $\hat {Q}(U, \sigma; U_0)<\mathcal {O}(|U|^{-1})$ as
$\hat {Q}(U, \sigma; U_0)<\mathcal {O}(|U|^{-1})$ as ![]() $| U|\to \infty$ because the normalization conditions of
$| U|\to \infty$ because the normalization conditions of ![]() $P$ and
$P$ and ![]() $P_{eq}$ give
$P_{eq}$ give
As mentioned above, ![]() $b(U)^2$ remains finite in the limit of
$b(U)^2$ remains finite in the limit of ![]() $U=-\infty$. Integrating (D 8) with respect to
$U=-\infty$. Integrating (D 8) with respect to ![]() $U$ from
$U$ from ![]() $-\infty$ gives
$-\infty$ gives
 \begin{equation} \frac{2m^2}{b^2(U)P_{eq}(U)}\left[-\varTheta(U-U_0)+\int_{-\infty}^U\,\textrm{d}U_1\ P_{eq}(U_1)\right] = \frac{\partial}{\partial U}\frac{\hat{Q}(U,0;U_0)}{P_{eq}(U) }. \end{equation}
\begin{equation} \frac{2m^2}{b^2(U)P_{eq}(U)}\left[-\varTheta(U-U_0)+\int_{-\infty}^U\,\textrm{d}U_1\ P_{eq}(U_1)\right] = \frac{\partial}{\partial U}\frac{\hat{Q}(U,0;U_0)}{P_{eq}(U) }. \end{equation}
Integrating (D 10) with respect to ![]() $U$ from a value smaller than
$U$ from a value smaller than ![]() $U_0$, substituting the result into (D 7) and using
$U_0$, substituting the result into (D 7) and using ![]() $\langle U_0 \rangle =0$, we arrive at
$\langle U_0 \rangle =0$, we arrive at
Interchanging the order of the integrals above, we use ![]() $\check {\gamma }(u)=\check {\gamma }(-u)$ to obtain (2.28).
$\check {\gamma }(u)=\check {\gamma }(-u)$ to obtain (2.28).
Some details on numerical calculations of (2.28) are mentioned below. We define ![]() $L$ as
$L$ as
We can choose ![]() $u_{c}(>0)$ so that
$u_{c}(>0)$ so that ![]() $|\check {\gamma }'(u)|$ is smaller than
$|\check {\gamma }'(u)|$ is smaller than ![]() $|\check {\gamma }'(u_{c})|$ for
$|\check {\gamma }'(u_{c})|$ for ![]() $u>u_{c}$. The integral in the square brackets of (2.28) is given by
$u>u_{c}$. The integral in the square brackets of (2.28) is given by ![]() $L(u, \infty )$. Using integration by parts, we obtain
$L(u, \infty )$. Using integration by parts, we obtain
 \begin{equation} L(u_{c},\infty)=\frac{\check{\gamma}(u_{c})}{2M}e^{-Mu_{c}^2}\left[1+ \frac{\textrm{e}^{Mu_{c}^2}}{\check{\gamma}(u_{c})} \int_{u_{c}}^{\infty} \,\textrm{d}u_1\ \check{\gamma}'(u_1) \textrm{e}^{-Mu_1^2}\right]. \end{equation}
\begin{equation} L(u_{c},\infty)=\frac{\check{\gamma}(u_{c})}{2M}e^{-Mu_{c}^2}\left[1+ \frac{\textrm{e}^{Mu_{c}^2}}{\check{\gamma}(u_{c})} \int_{u_{c}}^{\infty} \,\textrm{d}u_1\ \check{\gamma}'(u_1) \textrm{e}^{-Mu_1^2}\right]. \end{equation}The absolute value of the second term in the square brackets above is smaller than
 \begin{equation} \frac{\left|\check{\gamma}'(u_{c})\right|{e}^{Mu_{c}^2}}{\check{\gamma}(u_{c})\sqrt{M}}\int_{u_{c}\sqrt{M}}^{\infty} \textrm{d}x\ e^{-x^2} \approx \frac{\left| \check{\gamma}'(u_{c})\right|}{2Mu_{c}\check{\gamma}(u_{c})}, \end{equation}
\begin{equation} \frac{\left|\check{\gamma}'(u_{c})\right|{e}^{Mu_{c}^2}}{\check{\gamma}(u_{c})\sqrt{M}}\int_{u_{c}\sqrt{M}}^{\infty} \textrm{d}x\ e^{-x^2} \approx \frac{\left| \check{\gamma}'(u_{c})\right|}{2Mu_{c}\check{\gamma}(u_{c})}, \end{equation}
where the approximation is good for ![]() $u_{c}\sqrt {M}\gtrsim 1$. In our numerical calculations, we choose
$u_{c}\sqrt {M}\gtrsim 1$. In our numerical calculations, we choose ![]() $u_{c}$ so that
$u_{c}$ so that ![]() $u_{c}\sqrt {M}\approx 4$, and find that the right-hand side above is smaller than
$u_{c}\sqrt {M}\approx 4$, and find that the right-hand side above is smaller than ![]() $10^{-3}$, which enables us to neglect the second term in the square brackets of (D 13).
$10^{-3}$, which enables us to neglect the second term in the square brackets of (D 13).
The integral with respect to ![]() $u$ in (2.28) is rewritten as
$u$ in (2.28) is rewritten as
 \begin{equation} \int_{0}^{u_{c}}\,\textrm{d}u\ \frac{e^{-3Mu^2/2}}{L(u,\infty)} +\int_{u_{c}}^{\infty}\,\textrm{d}u \frac{e^{-3Mu^2/2}}{L(u,\infty)} , \end{equation}
\begin{equation} \int_{0}^{u_{c}}\,\textrm{d}u\ \frac{e^{-3Mu^2/2}}{L(u,\infty)} +\int_{u_{c}}^{\infty}\,\textrm{d}u \frac{e^{-3Mu^2/2}}{L(u,\infty)} , \end{equation}
where ![]() $u_{c}$ is chosen as indicated above. In the first term above, we can use
$u_{c}$ is chosen as indicated above. In the first term above, we can use
In the second term of (D 15), because of ![]() $u>u_{c}$,
$u>u_{c}$, ![]() $L(u,\infty )$ can be approximated to be the second term on the right-hand side of (D 16) with
$L(u,\infty )$ can be approximated to be the second term on the right-hand side of (D 16) with ![]() $u_{c}$ being replaced by
$u_{c}$ being replaced by ![]() $u$ for the same reason as described in the preceding paragraph. Thus, the second term of (D 15) is approximately equal to
$u$ for the same reason as described in the preceding paragraph. Thus, the second term of (D 15) is approximately equal to
Here, we use ![]() $\check {\gamma }(u_{c})\approx \check {\gamma }(\infty )$. In our numerical calculation, with
$\check {\gamma }(u_{c})\approx \check {\gamma }(\infty )$. In our numerical calculation, with ![]() $u_{c}$ being chosen as indicated above, the ratio of (D 17) to the first term of (D 15) is much smaller than
$u_{c}$ being chosen as indicated above, the ratio of (D 17) to the first term of (D 15) is much smaller than ![]() $10^{-3}$, and thus the first term is regarded as equal to the integral with respect to
$10^{-3}$, and thus the first term is regarded as equal to the integral with respect to ![]() $u$ in (2.28). Hence, we can calculate (2.28) by using
$u$ in (2.28). Hence, we can calculate (2.28) by using ![]() $\check {\gamma }(u)$ with
$\check {\gamma }(u)$ with ![]() $u\le u_{c}$, or in other words, by using
$u\le u_{c}$, or in other words, by using ![]() $\gamma (U)$ with
$\gamma (U)$ with ![]() $U$ smaller than
$U$ smaller than ![]() $4\bar {U}$ approximately. Thanks to this effective cutoff speed, our calculation results are free from the details of the rule for a large particle speed, as checked quantitatively in § 3.
$4\bar {U}$ approximately. Thanks to this effective cutoff speed, our calculation results are free from the details of the rule for a large particle speed, as checked quantitatively in § 3.
Appendix E. Renormalization correction under the shear effect
A simple shear flow in four dimensions is used in the calculation mentioned above (A 5). The components of its velocity gradient with respect to the Cartesian coordinates vanish except for ![]() $\nabla _2v_1$, which is a positive constant. As mentioned at the end of appendix A, the singular part of the viscosity changes as
$\nabla _2v_1$, which is a positive constant. As mentioned at the end of appendix A, the singular part of the viscosity changes as ![]() $k$ decreases from
$k$ decreases from ![]() $k_{o}$. The ratio of the change in the later stage with
$k_{o}$. The ratio of the change in the later stage with ![]() $k<k_{s}$, to the change in the earlier stage with
$k<k_{s}$, to the change in the earlier stage with ![]() $k>k_{s},$ is given by the second term in the square brackets of (4.64) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979). To evaluate this ratio, we take average of the term over the orthogonal components and average over the directions of the wavenumber vector. The former average is obtained by dividing (4.65) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979) by three – the dimension of the divergence-free space. In this equation, the dot immediately after the fraction should be deleted to validate the equality, and the right-hand side, as it is, represents the trace of the left-hand side. The latter average is obtained by replacing
$k>k_{s},$ is given by the second term in the square brackets of (4.64) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979). To evaluate this ratio, we take average of the term over the orthogonal components and average over the directions of the wavenumber vector. The former average is obtained by dividing (4.65) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979) by three – the dimension of the divergence-free space. In this equation, the dot immediately after the fraction should be deleted to validate the equality, and the right-hand side, as it is, represents the trace of the left-hand side. The latter average is obtained by replacing ![]() $\hat {\boldsymbol {k}}$ in (4.65) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979) by one of the four orthogonal unit vectors, summing the results over the four vectors, and dividing the sum by the spatial dimension, four. The result derived from theses averages is denoted by
$\hat {\boldsymbol {k}}$ in (4.65) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979) by one of the four orthogonal unit vectors, summing the results over the four vectors, and dividing the sum by the spatial dimension, four. The result derived from theses averages is denoted by ![]() $\delta _{s}$. As in deriving the right-hand side of (3.6) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979), we use the method of characteristics to find
$\delta _{s}$. As in deriving the right-hand side of (3.6) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979), we use the method of characteristics to find ![]() $\delta _{s}$ to be given by
$\delta _{s}$ to be given by ![]() $4\epsilon /(19{\rm \pi} ^2)$ multiplied by the integral of
$4\epsilon /(19{\rm \pi} ^2)$ multiplied by the integral of
with respect to the four-dimensional vector ![]() $\boldsymbol {q}$ over half the unit sphere with
$\boldsymbol {q}$ over half the unit sphere with ![]() $q_1>0$, where
$q_1>0$, where ![]() $I(\boldsymbol {q})$ is defined as the integral of the following integrand over
$I(\boldsymbol {q})$ is defined as the integral of the following integrand over ![]() $p$ running from
$p$ running from ![]() $q_2$ to
$q_2$ to ![]() $\infty$. The integrand is given by
$\infty$. The integrand is given by
divided by ![]() $(0.97 \vert q_1\vert ^{2/5} +q_1^2+p^2+q_3^2+q_4^2)^2$. If we replace this denominator by
$(0.97 \vert q_1\vert ^{2/5} +q_1^2+p^2+q_3^2+q_4^2)^2$. If we replace this denominator by ![]() $q^4$, where
$q^4$, where ![]() $q$ denotes
$q$ denotes ![]() $|\boldsymbol {q}|$, (E 1) becomes larger. Putting
$|\boldsymbol {q}|$, (E 1) becomes larger. Putting ![]() $q_3=q_4=0$ and changing the variable
$q_3=q_4=0$ and changing the variable ![]() $p$ to
$p$ to ![]() $Z\equiv 2(p-q_2)/q_1$ in (E 2), we obtain a new exponential function. Its integral over
$Z\equiv 2(p-q_2)/q_1$ in (E 2), we obtain a new exponential function. Its integral over ![]() $0<Z<\infty$ is denoted by
$0<Z<\infty$ is denoted by ![]() $I_1(q_1,q_2)$, and we have
$I_1(q_1,q_2)$, and we have
where the integral is taken over half the unit sphere mentioned above. In the square brackets of (E 2) after the above-mentioned conversion, the leading term for large ![]() $Z$ is given by
$Z$ is given by ![]() $-q_1^4Z^5/80$. Thus, as
$-q_1^4Z^5/80$. Thus, as ![]() $q_1$ approaches zero from the positive side, the leading term of
$q_1$ approaches zero from the positive side, the leading term of ![]() $I_1(q_1,q_2)$ is proportional to
$I_1(q_1,q_2)$ is proportional to ![]() $q_1^{-4/5}$, which justifies that we neglected the contribution from the integrand with
$q_1^{-4/5}$, which justifies that we neglected the contribution from the integrand with ![]() $q_1=0$ to the integral of (E 1). This integral shows
$q_1=0$ to the integral of (E 1). This integral shows ![]() $\delta _{s}>0$.
$\delta _{s}>0$.
Introducing the polar coordinates of ![]() $\boldsymbol {q}$, we can numerically perform the integral of (E 3) over the angular components. We write
$\boldsymbol {q}$, we can numerically perform the integral of (E 3) over the angular components. We write ![]() $J(q,Z)$ for the result, and have
$J(q,Z)$ for the result, and have
If we retain only the leading term in (E 2), ![]() $J(q,Z)$ in (E 4) is replaced by
$J(q,Z)$ in (E 4) is replaced by
where ![]() $\theta _1$ is defined so that
$\theta _1$ is defined so that ![]() $q_1=q\cos {\theta _1}$ holds. The integral in (E 5) can be expressed in terms of generalized hypergeometric functions, and the integral of
$q_1=q\cos {\theta _1}$ holds. The integral in (E 5) can be expressed in terms of generalized hypergeometric functions, and the integral of ![]() $J_1(q,Z)$ over
$J_1(q,Z)$ over ![]() $0<Z<\infty$ turns out to be proportional to
$0<Z<\infty$ turns out to be proportional to ![]() $q^{11/5}$, according to Mathematica (Wolfram Research). Numerically,
$q^{11/5}$, according to Mathematica (Wolfram Research). Numerically, ![]() $J(q,Z)$ is shown in figure 8 to be smaller than
$J(q,Z)$ is shown in figure 8 to be smaller than ![]() $J_1(q,Z)$. The double integral in (E 4) with
$J_1(q,Z)$. The double integral in (E 4) with ![]() $J$ replaced by
$J$ replaced by ![]() $J_1$ equals
$J_1$ equals ![]() $3.44$, which leads to
$3.44$, which leads to ![]() $0<\delta _{s}<7.33\times 10^{-2}\epsilon$.
$0<\delta _{s}<7.33\times 10^{-2}\epsilon$.

Figure 8. From the top, three solid curves, respectively, represent ![]() $J_1(1.0,Z), J_1(0.5,Z)$ and
$J_1(1.0,Z), J_1(0.5,Z)$ and ![]() $J_1(0.05,Z)$, while three series of circles, respectively, represent
$J_1(0.05,Z)$, while three series of circles, respectively, represent ![]() $J(1.0,Z), J(0.5,Z)$ and
$J(1.0,Z), J(0.5,Z)$ and ![]() $J(0.05,Z)$. We calculate
$J(0.05,Z)$. We calculate ![]() $J(q,Z)$ by means of numerical integration in Mathematica (Wolfram Research) with Method
$J(q,Z)$ by means of numerical integration in Mathematica (Wolfram Research) with Method ![]() $\to \{$‘GlobalAdaptive’, ‘MaxErrorIncreases’
$\to \{$‘GlobalAdaptive’, ‘MaxErrorIncreases’ ![]() $\to 10\,000$, Method
$\to 10\,000$, Method ![]() $\to$ ‘GaussKronrodRule’
$\to$ ‘GaussKronrodRule’![]() $\}$, MaxRecursion
$\}$, MaxRecursion ![]() $\to 20$.
$\to 20$.
In a pure-extension flow in four dimensions, the off-diagonal elements of the velocity gradient vanish and ![]() $\nabla _1 v_1=-3\nabla _2v_2=-3\nabla _3v_3=-3\nabla _4v_4$ is a positive constant. For this flow, we below evaluate the ratio of the changes in the later and earlier stages by taking averages in the same way as mentioned above, and write
$\nabla _1 v_1=-3\nabla _2v_2=-3\nabla _3v_3=-3\nabla _4v_4$ is a positive constant. For this flow, we below evaluate the ratio of the changes in the later and earlier stages by taking averages in the same way as mentioned above, and write ![]() $\delta _{e}$ for the result corresponding with
$\delta _{e}$ for the result corresponding with ![]() $\delta _{s}$. The ratio should be given by (4.65) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979) with the denominator being replaced by
$\delta _{s}$. The ratio should be given by (4.65) of Onuki & Kawasaki (Reference Onuki and Kawasaki1979) with the denominator being replaced by ![]() $q^4-(q_1/2)\partial _{q_1}+(q_2/6)\partial _{q_2}+ (q_3/6)\partial _{q_3}+ (q_4/6)\partial _{q_4}$ and with the expression of the normalized susceptibility, denoted by
$q^4-(q_1/2)\partial _{q_1}+(q_2/6)\partial _{q_2}+ (q_3/6)\partial _{q_3}+ (q_4/6)\partial _{q_4}$ and with the expression of the normalized susceptibility, denoted by ![]() $\chi ^*(\boldsymbol {q})$, being replaced by the one for the flow considered here. With the aid of (3.4) of Onuki & Kawasaki (Reference Onuki and Kawasaki1980a),
$\chi ^*(\boldsymbol {q})$, being replaced by the one for the flow considered here. With the aid of (3.4) of Onuki & Kawasaki (Reference Onuki and Kawasaki1980a), ![]() $\chi ^*(\boldsymbol {q})$ is approximated to be
$\chi ^*(\boldsymbol {q})$ is approximated to be ![]() $\sqrt {{\rm \pi} /2}$ for
$\sqrt {{\rm \pi} /2}$ for ![]() $q_1\ne 0$ in the pure-extension flow, as is consistent with (3.23b) of Onuki & Kawasaki (Reference Onuki and Kawasaki1980c). Thus, we find
$q_1\ne 0$ in the pure-extension flow, as is consistent with (3.23b) of Onuki & Kawasaki (Reference Onuki and Kawasaki1980c). Thus, we find ![]() $\delta _{e}$ to be given by
$\delta _{e}$ to be given by ![]() $4\epsilon /(19{\rm \pi} ^2)$ multiplied by the double integral of the following integrand over the unit sphere of the four-dimensional vector
$4\epsilon /(19{\rm \pi} ^2)$ multiplied by the double integral of the following integrand over the unit sphere of the four-dimensional vector ![]() $\boldsymbol {q}$ and over
$\boldsymbol {q}$ and over ![]() ${w}=0$ to
${w}=0$ to ![]() $\infty$. With
$\infty$. With ![]() $q_{\perp }^2$ denoting
$q_{\perp }^2$ denoting ![]() $q^2-q_1^2\equiv q^2\sin ^2{\theta _1}$, the integrand is the product of
$q^2-q_1^2\equiv q^2\sin ^2{\theta _1}$, the integrand is the product of
which is larger if we delete the last two terms in the square brackets, and
which is larger if we replace ![]() $e^{-2{w}/3}$ with
$e^{-2{w}/3}$ with ![]() $e^{2{w}/3}$ in the second term in the square brackets. This expression shows
$e^{2{w}/3}$ in the second term in the square brackets. This expression shows ![]() $\delta _{e}>0$. Using a new variable
$\delta _{e}>0$. Using a new variable ![]() $\zeta _1\equiv e^{2{w}/3}$, and performing the integration with respect to the angular components of
$\zeta _1\equiv e^{2{w}/3}$, and performing the integration with respect to the angular components of ![]() $\boldsymbol {q}$ other than
$\boldsymbol {q}$ other than ![]() $\theta _1$, we have
$\theta _1$, we have
Here, ![]() $I_3(q,\theta _1)$ is defined as the integral of
$I_3(q,\theta _1)$ is defined as the integral of ![]() $\exp {[-q^4(\zeta _1^6-1) (\cos ^4{\theta _1})/2]}$ over
$\exp {[-q^4(\zeta _1^6-1) (\cos ^4{\theta _1})/2]}$ over ![]() $\zeta _1=1$ to
$\zeta _1=1$ to ![]() $\infty$. This integral is written in terms of the generalized exponential integral function, while the integration with respect to
$\infty$. This integral is written in terms of the generalized exponential integral function, while the integration with respect to ![]() $\theta _1$ in (E 8) yields an expression involving generalized hypergeometric functions, according to Mathematica (Wolfram Research). Here, we note that
$\theta _1$ in (E 8) yields an expression involving generalized hypergeometric functions, according to Mathematica (Wolfram Research). Here, we note that ![]() $q^7I_3(q,\theta _1)$ tends to
$q^7I_3(q,\theta _1)$ tends to ![]() $0$ as
$0$ as ![]() $q$ approaches zero, and that
$q$ approaches zero, and that ![]() $I_3(q,\theta _1)$ diverges, more slowly than
$I_3(q,\theta _1)$ diverges, more slowly than ![]() $1/\vert \theta _1-{\rm \pi} /2\vert$, as
$1/\vert \theta _1-{\rm \pi} /2\vert$, as ![]() $\theta _1$ approaches
$\theta _1$ approaches ![]() ${\rm \pi} /2$. We thus have
${\rm \pi} /2$. We thus have ![]() $0<\delta _{e}<4.00\times 10^{-2}\epsilon$.
$0<\delta _{e}<4.00\times 10^{-2}\epsilon$.