Published online by Cambridge University Press: 09 October 2013
We present a theoretical and experimental study of the propagation of gravity currents in porous media with variations in the topography over which they flow, motivated in part by the sequestration of carbon dioxide in saline aquifers. We consider cases where the height of the topography slopes upwards in the direction of the flow and is proportional to the 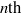 $n\text{th} $ power of the horizontal distance from a line or point source of a constant volumetric flux. In two-dimensional cases with
$n\text{th} $ power of the horizontal distance from a line or point source of a constant volumetric flux. In two-dimensional cases with 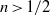 $n\gt 1/ 2$, the current evolves from a self-similar form at early times, when the effects of variations in topography are negligible, towards a late-time regime that has an approximately horizontal upper surface and whose evolution is dictated entirely by the geometry of the topography. For
$n\gt 1/ 2$, the current evolves from a self-similar form at early times, when the effects of variations in topography are negligible, towards a late-time regime that has an approximately horizontal upper surface and whose evolution is dictated entirely by the geometry of the topography. For 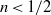 $n\lt 1/ 2$, the transition between these flow regimes is reversed. We compare our theoretical results in the case
$n\lt 1/ 2$, the transition between these flow regimes is reversed. We compare our theoretical results in the case 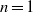 $n= 1$ with data from a series of laboratory experiments in which viscous glycerine is injected into an inclined Hele-Shaw cell, obtaining good agreement between the theoretical results and the experimental data. In the case of axisymmetric topography, all topographic exponents
$n= 1$ with data from a series of laboratory experiments in which viscous glycerine is injected into an inclined Hele-Shaw cell, obtaining good agreement between the theoretical results and the experimental data. In the case of axisymmetric topography, all topographic exponents 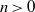 $n\gt 0$ result in a transition from an early-time similarity solution towards a topographically controlled regime that has an approximately horizontal free surface. We also analyse the evolution over topography that can vary with different curvatures and topographic exponents between the two horizontal dimensions, finding that the flow transitions towards a horizontally topped regime at a rate which depends strongly on the ratio of the curvatures along the principle axes. Finally, we apply our mathematical solutions to the geophysical setting at the Sleipner field, concluding that topographic influence is unlikely to explain the observed non-axisymmetric flow.
$n\gt 0$ result in a transition from an early-time similarity solution towards a topographically controlled regime that has an approximately horizontal free surface. We also analyse the evolution over topography that can vary with different curvatures and topographic exponents between the two horizontal dimensions, finding that the flow transitions towards a horizontally topped regime at a rate which depends strongly on the ratio of the curvatures along the principle axes. Finally, we apply our mathematical solutions to the geophysical setting at the Sleipner field, concluding that topographic influence is unlikely to explain the observed non-axisymmetric flow.