Hostname: page-component-5c6d5d7d68-wpx84 Total loading time: 0 Render date: 2024-08-27T11:39:03.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Vibration-induced wall–bubble interactions under zero-gravity conditions

Published online by Cambridge University Press:  27 August 2024

D.V. Lyubimov ,
T.P. Lyubimova Open the ORCID record for T.P. Lyubimova [Opens in a new window] ,
S. Meradji Open the ORCID record for S. Meradji [Opens in a new window]  and
B. Roux
D.V. Lyubimov
Affiliation:
Department of Theoretical Physics, Perm State University, 614990 Perm, Russia
T.P. Lyubimova*
Affiliation:
Department of Theoretical Physics, Perm State University, 614990 Perm, Russia Institute of Continuous Media Mechanics, Ural Branch of the Russian Academy of Science, 614013 Perm, Russia
S. Meradji
Affiliation:
Laboratoire IMATH - EA 2134, Université de Toulon, 83160 Toulon, France
B. Roux
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, M2P2 UMR 7340, 13451 Marseille, France
*
†Email address for correspondence: lubimova@psu.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

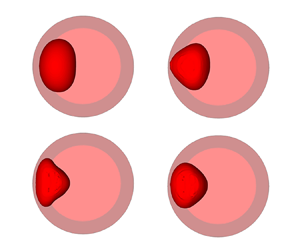
This work is devoted to a theoretical and numerical study of the dynamics of a two-phase system vapour bubble in equilibrium with its liquid phase under translational vibrations in the absence of gravity. The bubble is initially located in the container centre. The liquid and vapour phases are considered as viscous and incompressible. Analysis focuses on the vibrational conditions used in experiments with the two-phase system SF$_6$ in the MIR space station and with the two-phase system para-Hydrogen (p-H$_2$) under magnetic compensation of Earth's gravity. These conditions correspond to small-amplitude high-frequency vibrations. Under vibrations, additionally to the forced oscillations, an average displacement of the bubble to the wall is observed due to an average vibrational attraction force related to the Bernoulli effect. Vibrational conditions for SF$_6$ correspond to much smaller average vibrational force (weak vibrations) than for p-H$_2$ (strong vibrations). For weak vibrations, the role of the initial vibration phase is crucial. The difference in the behaviour at different initial phases is explained using a simple mechanical model. For strong vibrations, the average displacement to the wall stops when the bubble reaches a quasi-equilibrium position where the resulting average force is zero. At large vibration velocity amplitudes this position is near the wall where the bubble performs only forced oscillations. At moderate vibration velocity amplitudes the bubble average displacement stops at a finite distance from the wall, then large-scale damped oscillations around this position accompanied by forced oscillations are observed. Bubble shape oscillations and the parametric resonance of forced oscillations are also studied.

JFM classification

Drops and Bubbles: Drops and Bubbles Interfacial Flows (free surface): Interfacial Flows (free surface) Instability: Instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 992 , 10 August 2024 , A7
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Basaran, O.A. 1992 Nonlinear oscillations of viscous liquid drops. J. Fluid Mech. 241, 169–198.CrossRefGoogle Scholar
Beysens, D. 2004 L'effet des vibrations sur la matière inhomogène: quelques études en apesanteur. C.R. Méc 332 (5–6), 457–465.CrossRefGoogle Scholar
Beysens, D. & Evesque, P. 2005 Vibrational phenomena in near-critical fluids and granular matter. In Topical Teams in the Life & Physical Sciences, Towards New Research Applications in Space. ESA Publication Division SP 1281, 6–23.Google Scholar
Brackbill, J.U., Koth, D.B. & Zemach, C. 1992 A continuum method for modeling surface tension. Comput. Phys. 100, 335–354.CrossRefGoogle Scholar
Chandrasekar, S. 1959 The oscillations of viscous liquid glob. Proc. Lond. Math. Soc. 9, 141–149.CrossRefGoogle Scholar
Chelomey, V.N. 1985 Paradoxes in mechanics caused by vibrations. Meccanica 20, 314–316.CrossRefGoogle Scholar
Datt, G. & Touzot, G. 1984 Une présentation de la méthode des éléments finis Collection Université de Compiègne. Maloine S.A. Editeur.Google Scholar
Ebo-Adou, A., Tuckerman, L.S., Shin, S., Chergui, J. & Juric, D. 2019 Faraday instability on a sphere: numerical simulation. J. Fluid Mech. 870, 433–459.CrossRefGoogle Scholar
Faraday, M. 1831 On a peculiar class acoustical figures and on certain forms assumed by a group of particles upon elastic surface. Phil. Trans. R. Soc Lond. 121, 209–318.Google Scholar
François, M.M., Cummins, S.J., Dendy, E.D., Kothe, D.B., Sicilian, J.M. & Williams, M.W. 2006 A balanced-force algorithm for continuous and sharp interfacial surface tension models within a volume tracking framework. J. Comput. Phys. 213, 141–173.CrossRefGoogle Scholar
Galusinski, C. & Vigneaux, P. 2008 On stability condition for bi-fluid flows with surface tension: application to microfluidics. J. Comput. Phys. 227, 6140–6164.CrossRefGoogle Scholar
Garrabos, Y., Beysens, D., Lecoutre, C., Dejoan, A., Polezhaev, V. & Emelianov, V. 2007 Thermoconvectional phenomena induced by vibrations in supercritical SF6 under weightlessness. Phys. Rev. E 75, 056317.CrossRefGoogle ScholarPubMed
Gresho, P.M., Lee, R.L. & Sani, R.L. 1980 On the time dependent solution of the incompressible Navier–Stokes equations in two and three dimensions. In Recent Advances in Numerical Methods in Fluids (ed. Taylor, C. & Morgan, K.), vol. 1, pp. 27–79.Google Scholar
Haroutunian, V., Engelman, M.S. & Hasbani, I. 1993 Segregated finite element algorithms for the numerical solution of large-scale incompressible flow problems. Intl J. Numer. Meth. Fluids 17, 323–348.CrossRefGoogle Scholar
Hassan, S., Lyubimova, T.P., Lyubimov, D.V. & Kawaji, M. 2006 Effects of vibrations on particle motion near a wall: existence of attraction force. Intl J. Multiphase Flow 32, 1037–1054.CrossRefGoogle Scholar
Hirt, C.W. & Nichols, B.D. 1981 Volume of Fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225.CrossRefGoogle Scholar
Ivanova, A.A. & Kozlov, V.G. 2014 Lift force acting on body in liquid in the vicinity of boundary executing tangential oscillations. Microgravity Sci. Technol. 26, 179–187.CrossRefGoogle Scholar
Jouers, C. 1986 Hydrogen Properties for Fusion Energy. University of California Press.Google Scholar
Klotsa, D., Swift, M.R., Bowley, R.M. & King, P. 2007 Interaction of spheres in oscillatory fluid flows. Phys. Rev. E 76, 056314.CrossRefGoogle ScholarPubMed
Kothe, D.B. & Mjolsness, R.C. 1992 RIPPLE: a new model for incompressible flows with free surfaces. AIAA J. 30, 2694–2700.CrossRefGoogle Scholar
Lamb, H. 1881 On the oscillations of a viscous spheroid. Proc. Lond. Math. Soc. 13, 51–66.CrossRefGoogle Scholar
Lee, C.P, Anilkumar, A.V. & Wang, T.G. 1994 Static shape of an acoustically levitated drop with wave-drop interaction. Phys. Fluids 6, 3554–3566.CrossRefGoogle Scholar
Liang, P.Y. 1991 Numerical method for calculation of surface tension flows in arbitrary grids. AIAA J. 29 (2), 161–167.CrossRefGoogle Scholar
Lugovtsov, B.A. & Sennitskiy, V.L. 1987 Motion of body in vibrating fluid. USSR Rept Eng Equipment. Transl. into English from Doklady Akademii Nauk SSSR (Moscow, USSR) 289, 1986, 314–317 289, 68.Google Scholar
Lundgren, T.S. & Mansour, N.N. 1988 Oscillation of drops in zero gravity with weak viscous effect. J. Fluid Mech. 194, 479–510.CrossRefGoogle Scholar
Lyubimov, D., Cherepanov, A. & Lyubimova, T. 1992 The motion of solid body in a liquid under the influence of a vibrational field. In Reviewed Proc. of the First Int. Symp. On Hydromechanics and Heat/Mass Transfer in Microgravity (ed. Avduevsky, V.S. & others), pp. 246–251. Gordon and Breach.Google Scholar
Lyubimov, D., Lyubimova, T. & Cherepanov, A. 1987 On a motion of solid body in a vibrating fluid. Convective Flows. Perm State University, 61–70.Google Scholar
Lyubimov, D.V., Cherepanov, A.A. & Lyubimova, T.P. 1996 Deformation of gas or drop inclusion in high frequency vibrational field. Microgravity Q. 6, 69–73.Google Scholar
Lyubimov, D.V., Cherepanov, A.A., Lyubimova, T.P. & Roux, B. 1997 Interface orienting by vibration. C.R. Acad. Sci. Paris IIB 325 (7), 391–396.Google Scholar
Lyubimov, D.V., Cherepanov, A.A., Lyubimova, T.P. & Roux, B. 2001 a Vibration influence of a two-phase system in weightlessness conditions. J. Phys. IV 11 (PR6), 83–90.Google Scholar
Lyubimov, D.V. & Lyubimova, T.P. 1990 A continuum method for the numerical solution of the problems with deformable fluid interfaces. Model. Mech. 4 (N1), 136–140.Google Scholar
Lyubimov, D.V., Lyubimova, T.P. & Cherepanov, A.A. 2003 Dynamics of Fluid Interfaces in Vibrational Fields. PhysMathLit.Google Scholar
Lyubimov, D.V., Lyubimova, T.P. & Cherepanov, A.A. 2021 Resonance oscillations of a drop (bubble) in a vibrating fluid. J. Fluid Mech. 909, A18.CrossRefGoogle Scholar
Lyubimov, D.V., Lyubimova, T.P., Cherepanov, A.A., Meradji, S., Roux, B., Beysens, D., Garrabos, Y. & Chatain, D. 2001 b 2D unsteady motion and deformation of a gaseous bubble in a vibrating liquid at zero gravity. J. Phys. IV 11 (PR6), 91–98.Google Scholar
Lyubimova, T.P. & Cherepanova, A. 2008 In Vibrational dynamics of bubbles suspended in a viscous liquid. In Proc. 3rd Int. Symp. on Physical Sciences in Space, Nara, Japan, 22–26 October, pp. 234–235. Gakkai.Google Scholar
Lyubimova, T.P., Lyubimov, D.V. & Shardin, M. 2011 The interaction of rigid cylinders in a low Reynolds number pulsational flow. Microgravity Sci. Technol. 23, 305–309.CrossRefGoogle Scholar
Marcout, R., Zwilling, J.-F., Laherrere, J.-M., Garrabos, Y. & Beysesn, D. 1995 ALICE 2, an advanced facility for the analysis of fluids close to their critical point in microgravity. Microgravity Q. 5, 162–170.Google Scholar
Marston, P.L. 1980 Shape oscillation and static deformation of drops and bubbles driven by modulated radiation stress: theory. J. Acoust. Soc. Am. 67, 15–26.CrossRefGoogle Scholar
Marston, P.L. & Apfel, R.E. 1980 Quadrupole resonance of drops driven by modulated acoustic radiation pressure: experimental properties. J. Acoust. Soc. Am. 67, 27–37.CrossRefGoogle Scholar
Mei, C.C. & Zhou, X. 1991 Parametric resonance of a spherical bubble. J. Fluid Mech. 229, 29–50.CrossRefGoogle Scholar
Meradji, S., Lyubimova, T.-P., Lyubimov, D.-V. & Roux, B. 2001 Numerical simulation of a liquid drop freely oscillating. Cryst. Res. Technol. 36 (7), 729–744.3.0.CO;2-3>CrossRefGoogle Scholar
Miles, J. & Henderson, D. 1990 Parametrically forced surface waves. Annu Rev. Fluid Mech. 22, 143–165.CrossRefGoogle Scholar
Myshkis, A.D., Babskii, V.-G., Kopachevskii, N.-D., Slobozhanin, L.A. & Tyoptsov, A.D. 1987 Low-Gravity Fluid Mechanics: Mathematical Theory of Capillary Phenomena, vol. 36, pp. 729–744. Springer.CrossRefGoogle Scholar
Polezhaev, V., Emelianov, V., Ivanov, A., Kalmykov, A., Beysesn, D. & Garrabos, Y. 2001 An experimental study of the effect of vibrations on supercritical fluid transfer processes under microgravity conditions. Cosmic Res. (translated from Kosm. Issled. 39, 201) 39, 187.Google Scholar
Popinet, S. 2018 Numerical models of surface tension. Annu. Rev. Fluid Mech. 50, 49–75.CrossRefGoogle Scholar
Rayleigh, Lord 1879 The capillary phenomena of jets. Proc. R. Soc. Lond. 29, 71–97.Google Scholar
Reid, W. 1960 The oscillations of a viscous liquid drop. Q. Appl. Maths 18, 86–89.CrossRefGoogle Scholar
Rider, W.J. & Kothe, D.B. 1998 Reconstructing volume tracking. J. Comput. Phys. 141, 112–152.CrossRefGoogle Scholar
Saad, Y. 2000 Iterative Methods for Sparse Linear Systems. PWS Publishing.Google Scholar
Saadatmand, M. & Kawaji, M. 2010 Effect of viscosity on vibration-induced motion of a spherical particle suspended in a fluid cell. Microgravity Sci. Technol. 22, 433–440.CrossRefGoogle Scholar
Schipitsyn, V. & Kozlov, V. 2020 Dynamics of a solid of nearly neutral buoyancy in cavity subjected to rotational vibrations. Phys. Fluids 32, 044102.CrossRefGoogle Scholar
Schmidt, G. 1975 Parameterregte Schwingungen. Web Deutcher Verlag der Wissenschaften.Google Scholar
Sennitskii, V.L. 1988 Motion of a gas bubble in a viscous vibrating liquid. J. Appl. Mech. Tech. Phys. 29, 865–870.CrossRefGoogle Scholar
Trinh, E.H. & Hsu, C.J. 1986 Equilibrium shapes of acoustically levitated drops. J. Acoust. Soc. Am. 79, 1335–1338.CrossRefGoogle Scholar
Wunenburger, R., Chatain, D., Garrabos, Y. & Beysens, D. 2000 Magnetic compensation of gravity forces in hydrogen near its critical point. Phys. Rev. E 62, 469–476.CrossRefGoogle ScholarPubMed
Zappoli, B., Beysens, D. & Garrabos, Y. 2015 Heat Transfer and Related Phenomena in Supercritical Fluids. Springer.CrossRefGoogle Scholar
Zienkiewicz, O.C., Taylor, R.L. & Zhu, J.Z. 2013 The Finite Element Method: Its Basis and Fundamentals, 7th edn. Butterworth-Heinemann Publishing.Google Scholar
Supplementary material: File

Lyubimov et al. supplementary material

Lyubimov et al. supplementary material
Download Lyubimov et al. supplementary material(File)
File 159.1 KB