1. Introduction
It has been shown by several authors that the scattering and emission processes in the microwave frequency region are affected by sub-surface inhomogeneities in the Greenland ice sheet (Reference ZwallyZwally, 1977; Reference Zwally and GloersenZwally and Gloerson, 1977; Reference Comiso, Zwally and SabaComiso and others, 1982; Reference Swift, Hayes, Herd, Jona and DelnoreSwift and others, 1985). These sub-surface features have been recorded by glaciologists and are one of several diagenetic facies, or physical and chemical characteristics, used to divide ice sheets into zones. In 1962, Reference BensonBenson (1962) determined that the Greenland ice sheet has ablation, soaked, percolation and dry-snow zones. Changes in Ku-band satellite radar-altimeter waveforms over the different diagenetic regions of Greenland have been noted and analyzed (Reference Ridley and PartingtonRidley and Partington 1988; Reference Partington, Ridley, Rapley and ZwallyPartington and others, 1989; Reference Davis and MooreDavis and Moore, 1993). These satellite waveforms show that returns from some areas of the ice sheet have both a surface- and volume-scattering component. The volume or sub-surface component is due to penetration of the Ku-band pulse into the ice sheet. Determining the amount of the radar return caused by surface reflection as opposed to sub-surface scattering is, however, very difficult. Another issue that needs more thorough analysis is the response of the radar to ice features in the percolation zone. A more in-depth understanding of the effects of the diagenetic zones on the radar-altimeter waveform will not only help determine if there are biases in altitude measurements due to penetration but will also allow mapping of the diagenetic boundaries.
In 1991, NASA conducted a multi-sensor airborne altimetry experiment over the Greenland ice sheet. This experiment was the first in a series of biennial experiments aimed at measuring small-scale changes in the topography and mass balance of the ice sheet and at understanding the effects of penetration of a Ku-band radar-altimeter pulse into the ice sheet. The NASA Advanced Application Flight Experiment (AAFE) Ku-band radar altimeter, refurbished by the Microwave Remote Sensing Laboratory at the University of Massachusetts in 1990, participated in this experiment along with the NASA Airborne Oceanographic Lidar (AOL), the NASA Airborne Terrain Laser Altimeter System (ATLAS) and the NASA Ka-hand Surface Contour Radar (SCR). The experiment consisted of 10 flights over the Greenland ice sheet between 22 August and 20 September 1991 aboard the NASA P-3 aircraft. Positional information provided by three Global Positioning System (GPS) receivers aboard the NASA P-3 was used to control the autopilot of the aircraft. This system allowed accurate positioning under the European Remote Sensing satellite (ERS-1) trajectory and enabled arcurate repeat missions on all flight lines. The missions were flown over the ice sheet from Sondreström Air Force Base (now known as Kangerlussuaq) on the west coast of Greenland at an average altitude of 400 m above the surface, and the flight lines covered an area between 65° and 75° N.
All of the remote-sensing radar and laser instruments provided information about the aircraft altitude above the ice sheet. The GPS receivers, on the other hand, calculated the aircraft altitude above the ellipsoid, which is a reference around the surface of the Earth. The between these two measurements is the actual ice-sheet altitude above the ellipsoid.
In 1993, the AAFE radar altimeter, AOL laser altimeter and ATLAS laser altimeter participated in the Greenland experiment again, along with the Coherent Antarctic Radar Depth Sounder (CARDS) built by the University of Kansas. Between 23 June and 9 July 1993, the NASA P-3 aircraft flew 11 missions that covered an area between 61° and 74° Ν on the ice sheet.
The 1991 and 1993 experimental flights over Greenland passed over the ablation, soaked, percolation and dry-snow diagenetic zones of the ice sheet. Since the airborne altimeter is unable to distinguish between the reflective characteristics of the ablation and soaked zones, these regions are referred to as one in this paper. As the six representative waveforms in Figure 1 show, the AAFE radar-altimeter returns received from the various zones differed significantly in shape. Each of the waveforms in Figure 1 is normalized in power with a single-range bin equivalent to 2.77 ns or 41.67 cm, and the latitude and longitude where each waveform was received, along with the ice altitude above the ellipsoid at that point, are noted. These variations in the waveform shape are due to differences in the scattering properties of the various zones of the ice sheet. Figure 2 shows the boundaries of the diagenetic zones in Greenland as well as the location on the ice sheet where each waveform was obtained. Waveforms 1 and 2, which have a large slope or sharp leading edge and a sharp trailing edge, come from the ablation and soaked zone, respectively. The trailing edges on waveform 3, which is from the percolation zone, has a smaller slope than waveforms 1 and 2, while the leading edges remain sharp, and waveform 4, also from the percolation zone, has a notable second peak. Waveforms 5 and 6, which were obtained near the summit in the dry-snow zone, still have a sharp leading edge but their trailing edge is long and gently sloping. These airborne-altimeter waveforms do not look like typical satellite-altimeter waveforms due to differences in beamwidth and size. These differences are explained in greater detail in the discussion and concluding remarks section of this paper.

Fig. 1. Six altimeter return waveforms obtained from the Greenland ice sheet during a September 1991 mission.

Fig. 2. Simplified distribution of the diagenetic zones in Greenland according to Benson, and the location of the altimeter six altimeter waveforms of Figure 1.
The interaction of the AAFE altimeter 13.9 GHz pulse with the different diagenetic zones can be determined by calculating the dielectric properties of the snow and the depth of penetration in each region. Since snow is a heterogeneous mixture of air, ice and liquid water, all of which have known dielectric constants, the dielectric constant of snow, ε s. can be approximated. Measurements in the microwave region show that, at a given frequency, ε s depends mainly on the density of the snow, ρ s, and the percentage of liquid-water content, m v. As the percentage of liquid-water content increases, both the real, ε′ s, and imaginary, ε′′ s, parts of the dielectric constant increase. An increase in density also caures an increase in the dielectric constant. This increase, however, mainly affects the real part of ε s. Dry snow, which has a liquid-water content of zero, has an ε′ s that depends only on the snow density, and on ε′′ s that depends on the snow density and on the dielectric constant of pure ice, ε i, at the measurement frequency (Reference Ulaby, Moore and FungUlaby and others, 1986). Models such as the Debye-like model and the Polder Van Santeen model can be used to calculate the dielectric constant of snow. For snow that has some water content, the Debye-like model approximates the dielectric constant, ε ws, as

where the effective relaxation frequency of wet snow, f o, is 9.07 GHz (Reference Hallikainen, Ulaby and AbdelrazikHallikanen and others, 1986). The Polder Van Santeen model approximates the dielectric constant of dry snow, ε ds, as

(Reference Ulaby, Moore and FungUlaby and others, 1986). Both models agree well with measured results (Reference Stiles and UlabyStiles and Ulaby, 1980; Reference Swift, Hayes, Herd, Jona and DelnoreUlaby and Stiles, 1980; Reference Hallikainen, Ulaby and AbdelrazikHallikainen and others, 1986). Once the dielectric constant of snow at 13.9 GHz has been estimated, the attenuation coefficient, α, and ilic depth of penetration, ρ p, at this frequency can be calculated using
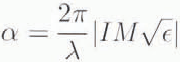
and
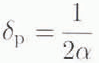
(Reference Ulaby, Moore and FungUlaby and others, 1982). When the depth of penetration is known, the type of scattering in the ablation, soaked, percolation and dry-snow zones can be determined and used to model the altimeter return waveform.
2. Scattering Models of the Diagenetic Zones of Greenland
A. Ablation- and Soaked-Zones Model
Studies of the ablation and soaked zones in Greenland reveal that the upper layers of snow are wet and dense due to summer melting. Measurements of snow density in the summer months range from 0.4 to 0.6 Mg m −3 (Reference BensonBenson, 1962) and the percentage of liquid-water content may be as high as 3%. Estimating the dielectric constant of the snow using tlie Debye-like model and then calculating α and ρ p with Equation (3) and (4) gives an attenuation coefficient greater than 21 Np m−1 or 186 dB m−1 and a depth of penetration less than 2.0 cm at 13.9 GHz. During the transitional season from the summer melting months of June and July to the winter season beginning around October, the ablation and soaked zones may not have a high water content but the snowpack will remain dense and still have a high attenuation coeficient. These approximate calculations of α and ρ p, show that there is little surface penetration at 13.9 GHz, even in August and September, and therefore radar-altimeter returns in these regions are predominantly dur to surface scattering.
Surface scattering from a randomly distributed rough surface has been described by Reference BrownBrown (1977) as the convolution of the flat-surface impulse response with the distribution of height scatterers. The flat-surface impulse response, P fs(t). is calculated by assuming a transmitted impulse and using the radar range equation

where the gain of the radar antenna is approximated as
(Barrirk, 1972). The barkscatter coefficient for the surface is

(Reference Jackson, Walton, Hines, Walter and PengJackson and others, 1992), where Γ(0°) is the power-reflection coefficient at nadir and s is the rms surface slope, but, for small incidence angles, it can be approximated by

Convolving P fs(t) with a Gaussian height distribution of scatterers with a standard deviation of σh, leads to a rough-surface impulse response of

where

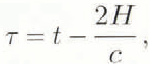
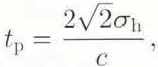

and erfc is the complementary error function (Reference Barrick and DerrBarrick, 1972; Reference BrownBrown, 1977). The total rough-surface system response is then calculated by couvolving the rough-surface impulse response with the system point-target response, which can he approximated as a Gaussian pulse with a 3 dB width of τp and a standard deviation of σp = 0.425τp (Reference BrownBrown, 1977). The result is the same as Equation (9), except t p is now defined as

The rms surface height, and σh surface slope, s, are the two surface parameters that determine the shape of the return waveform. A change in σh, affects the slope of the leading edge of the return waveform, while a change in s affects the slope of the trailing edge. Τo determine values of σh, s and Η or range, AAFE return waveforms are fitted using the least-mean-squared error (LMSE) method (Reference Carnahan, Luther and WilkesCarnahan and others, 1969; Reference Press, Flannery, Teukolsky and VetterlingPress and others, 1988) to a non-linear five-parameter model, which is Equation (9) plus a parameter, a, representing the noise floor of the waveform, or

Altimeter waveforms from the ablation and soaked zones have the same shape as the model in Equation (15). When the surface-scattering model is fitted to waveform 2 of Figure 1, as shown in Figure 3a, the LMSE fit yields a σh of 0.12 m and an s of 5.8°. In the percolation Lone, however, return waveforms, such as waveforms 3 and 4 of Figure 1, do not look like typical surface-scattering returns. Waveform 4, shown in Figure 3b along with the model fit, has a trailing edge that differs considerably from a surface-scattering waveform, and therefore the values of s are not relevant. Although waveforms in the dry-snow zone, such as waveform 6 in Figure 1, look like surface-scatteting returns, fitting them to the surface-scattering model, as shown in Figure 3c, results in abnormally high values of s. It is unlikely that surface scattering is the only component contributing to the return waveform in the percolation and dry-snow zones.
Even though the trailing edge of the waveform is sensitive to the different diagenetic zones of the ice sheet, there is always a surface component in the return due to the dielectric interface between the air and the snowpack. This return from the surface creates the sharp leading edge shown in all of the waveforms in Figure 1. Since the rms surface height, σh, is determined from the leading edge of the return, it can be measured by fitting Equation (15) to AAFE waveforms. Figure 4a shows the ice altitudes from a southwest to northeast pass over the ice sheet and Figure 4b shows the corresponding rms surface-height values over the flight line, wherr each measurement represents a fit to 960 averaged waveforms. The average rms surface height over this section of the ice sheet is 42 cm and the standard deviation from the mean is 33 cm. Figure 4b also shows the approximate location of the diagenetic transitions and the mean and standard deviation of the rms surface height for each individual diagenetic region of the ice sheet. The higher values for σh, in the ablation and soaked zones correspond to the greater variability in ice altitude in Figure 4a, while the lower values in the dry-snow zone correspond to the smoother ice altitudes.

Fig. 4. Measurements of the rms surface height over a southwest to northeast flight line, (a) The actual altitudes measured and (b) the rms surface height determined by fitting 960 averaged waveforms to the surface-scatterinç model in Equation (15).
Since the trailing edge of the altimeter waveform is sub-surface and volume scattering, the rms surface slope, s, cannot be determined by fitting return waveforms from the percolation and dry-snow zones to a surface-scattering model. Returns from the ablation and soaked zones, however, are predominantly due to surface scattering and therefore can he used to measure s. Figure 5a shows the ice altitudes over a section of the ablation and soaked zones and Figure 5b shows the corresponding rms surface-slope values resulting from fitting Equation (15) to AAFE return waveforms. Since a value of s greater than or equal to 15.6° represents a full antenna beam (see Discussion and Concluding Remarks for details), any s greater than this is meaningless. Over flight section, the average and standard deviation of s are 9.0° and 3.6°, respectively, but these slopes appear to he higher than expected. Since typical ocean rms slope values range between 5° and 8° (Reference Jackson, Walton, Hines, Walter and PengJackson and others, 1992), expected ice values for s would be even smaller. The trailing edge of the return waveform is also affected by aircraft mispointing angle and slope-induced error, which is the error induced on the return waveform due to a sloping surface within the radar-altimeter footprint (Reference Brenner, Bindschadler, Thomas and ZwallyBrenner and others, 1983). Both mispointing angle and slope-induced error make the trailing edge of the waveform extend out farther and therefore create a larger value of s when the waveform is fitted to the surface-scattering model. Since the average mispointing angle over the flight section is less than 1.2° and the more reasonable values of s correspond to the flat regions in Figure 5a while the high values correspond to the high slope areas, it is quite probable that the high values of s are the result of slope-induced error. For aircraft radar-altimeter measurements, these errors only affect the shape of the trailing edge and therefore, if they are not exceptionally large, they do not affect the range measurement, which is taken from the leading edge.

Fig. 5. Measurements of the rmr surface slope over a flight section in the ablation and soaked zones, (a) The actual altitudes measured and (b) the rms surface slope determined by fitting 960 averaged waveforms to the surface-scattering model in Equation (15).
B. Percolation-Zone Model
In the percolation zone, where there is some summer melting, liquid water percolates down into the sub-surface snow and refreezes into ice layers, ice pipes and ice lenses. Stratigraphic studies reveal that these ice structures are located anywhere between 0.1 and 5 m below the ice-sheet surface (Reference BensonBenson, 1962). Since this zone is a transition region between the soaked and dry-snow zones, the liquid-water content may vary from 3% near the border of the soaked zone to 0% near the dry-snow zone. Similarly, the density of the snow may range from 0.5 to 0.3 Mg m−3. Such a large change in the snow properties results in a vast range uf attenuation co-effficients and depths of penetration in this region.
The numerous odd-shaped sub-surface structures in the percolation zone, as well as the range of penetration depths, make it more difficult to model than the soaked and ablation zones. As the four altimeter return waveforms in Figure 6 show, the sub-surface ice features in the percolation zone affect the waveform shape. Since the ice lenses, pipes and layers are usually greater than 10 cm in diameter and are large relative to the 2.16 cm altimeter wavelength, the resulting scatter from these ice structures is in the optical regime or the geometric optics limit (Reference Ulaby, Moore and FungUlaby and others, 1981). Therefore, the return from the ice features dominates any scattering from the surrounding snow, and the percolation zone can be modeled as large volume-scatterers in a constant dielectric medium. As a result, the radar-altimeter return is calculated using the volume-scattering radar-range equation (Reference Swift, Hayes, Herd, Jona and DelnoreSwift and others, 1985), which is

where the antenna gain G(θ) is defined in Equation (6), Τ is the power-transmission coefficient, R
o is the distance from the radar to the surface, R is a variable representing the range to the sub-surface scatterers and ![]() is the velocity of propagation in the snow. This analysis is carried out in cylindrical coordinates and therefore dV = ρd ρd03D5;dh where h is the depth below the surface. The extinction coefficient, κ
e, is defined as the sum of the power-absorption coefficient, κ
e, and the power-scattering coefficient, κ
s, or κ
e = κ
a + κ
s. Since the scattering losses in snow are negligible relative to the absorption losses at frequencies below 15 GHz (Reference Stiles and UlabyStiles and Ulaby, 1981; Reference Hallikainen, Ulaby and AbdelrazikHallikainen and others, 1986), κ
e for the percolation zone is
is the velocity of propagation in the snow. This analysis is carried out in cylindrical coordinates and therefore dV = ρd ρd03D5;dh where h is the depth below the surface. The extinction coefficient, κ
e, is defined as the sum of the power-absorption coefficient, κ
e, and the power-scattering coefficient, κ
s, or κ
e = κ
a + κ
s. Since the scattering losses in snow are negligible relative to the absorption losses at frequencies below 15 GHz (Reference Stiles and UlabyStiles and Ulaby, 1981; Reference Hallikainen, Ulaby and AbdelrazikHallikainen and others, 1986), κ
e for the percolation zone is
where α is the attenuation coefficient of the snow. Thus, the exponential component in Equation (16) represents the two-way power attenuation in the lossy dielectric media.

Fig. 6. Four sample altimeter return waveforms from the central part of the percolation zone of Greenland obtained during a September 1991 mission.
The volume-backscatter coefficient, η v. in Equation (16) is due to the ice lenses, pipes and layers and is defined as the product of σ B, the backscatter cross-section per particle and n, the density per unit volume, or
(Reference Swift, Hayes, Herd, Jona and DelnoreSwift and others, 1985). In the percolation zone, however, the ice features are not distributed evenly with depth and may be larger at certain depths. Therefore,
assuming independence of ϕ. For a first-order approximation, the distribution is assumed to be independent of ρ resulting in n(h) and σ B(h).
Substituting these results into Equation (16) and performing the integral gives

where C 1 and τ are defined as

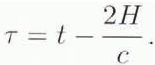
In the percolation zone, the surface backscatter component of the altimeter return waveform is due to the air-snow boundary, while the volume backscatter component is due to the optical volume scattering in the sub-surface snow. As a result, the total return power, P r(τ), is the incoherent Mini of these two components.
where A and Β are the percentages of surface- and volume-return power, respectively.
To determine the volume-scattering component of the radar return, it is important to know the distribution of n and σB vs depth. Unfortunately, there is limited documentation on these parameters due to the difficulty in obtaining the measurements. Thus, in the 1993 Greenland ground-truth experiment at Dye 2, a sample distribution of ice layers, lenses and pipes was obtained. A 5 m by 3 m area of the ice sheet was probed at 10 cm increments using a marked steel rod which was pressed into the snowpack until it hit ice. The raw data from this experiment are shown in Figure 7. To validate this probing experiment, a pit was dug alongside the 5 m by 3 m area and each 10 cm vertical wall was documented for size and location of ice features.

Fig. 7. A sample distribution of the ice features in a 5 m by 3 m area of the Greenland ice sheet at Dye 2. Each measurement represents the depth that the steel rod hit ice.
As Figure 7 shows, there was a continuous ice layer at a depth of 1 m and the thickness of this layer fluctuated between 1 and 3 cm. Other sample pits dug several hundred meters away from this pit also had an ice layer at a depth of 1 m. This layer may have been the surface from a previous summer and it shows that some ice layers in the percolation zone may extend over very large areas. The results from this probing experiment were used to create the sample distribution of n(h) shown in Figure 8. It is clear from this sample that the ice features do not have a standard distribution. In this case, they tended to be located between 37 and 42 cm, between 46 and 49 cm, between 59 and 61 cm, between 65 and 70 cm and between 78 and 81 cm. The ice layer at 1 m is not included in this distribution.

Fig. 8. A sample distribution of the location of ice features below the surface or n(h) in the Greenland snow pack at Dye 2.
Determining the backscatter coefficient σB is as difficult as calculating n(h) Figure 9 is a picture taken the 1993 Greenland experiment of an ice pipe leading down to an ice lens. Since the AAFE altimeter is nadir-viewing, these ice features would be viewed by the instrument from their top surface. In the optical regime, a target with gradual curving surfaces and an arbitrary shape has a backscatter coefficient of
where r(0) is the reflection coefficient at normal incidence and α1 and α2 are the radii of curvature in the two planes of observation (Reference Swift, Hayes, Herd, Jona and DelnoreSwift and others, 1985). Density measurements of the ice features taken during the 1993 experiment were between 0.86 and 0.91 Mg m−3. Since this is very close to the density of pure ice, which is 0.916 Mg m−3, the dielectric constant of pure ire, ε i, may be used to calculate r(0) or

Using ground-truth measurements of snow density and water content along with the Debye-like model in Equation (1) to approximate the dielectric constant of the surrounding snow results in ε s values ranging from 1.76 + j.001 to 1.83 + j.05 and an r(0) between 0.13–j.006 and 0.17–j.008.

Fig. 9. Picture of an ice pipe and an icr lens taken during the 1993 Greenland ground-truth experiment at Dye 2.
Ice pipes in the percolation zone are typically 4–7 cm in diameter and their size is independent of depth in the first meter cf the snowpack. In addition, since they are viewed by the radar altimeter from their top surface, they appear to be circular. Therefore, the average backscatter cross-section of an ice pipe in the percolation zone is σ B ice pipe(h) = σ B ice pipe ≈ –28 dBsm. The ice lenses, on the other hand, are larger at greater depths. Lenses within 60 cm cf the surface are typically 10–20 cm in diameter, while those closer to 80 cm are often 50–60 cm in diameter. The resulting average backscatter cross-section for such ice lenses is σ B ice lens(h = 60 cm) ≈ –20 dBsm and σ B ice lens(h = 80cm) ≈ –8 dBsm. Finally, a continuous ice layer, such as the one throughout the Dye 2 area located at 1 m, is larger than the area of the AAFE footprint, and therefore its backscatter cross-section is limited by the footprint area to σ B ice layer(h – 1 m) ≈ 20dBsm. Since the ice feature with the largest contributing backscatter cross-section in the percolation zone is the continuous ice layer, it is the scatterer, but the ice lenses and pipes are closer to the surface, and the incoming signal is not attenuated as much before it interacts with them.
Although these ground-truth data give an idea of the size and distribution of ice features, they represent only one sample in the percolation zone, which covers a large area of the ice sheet. These results can be inserted into Equation (21), however, to get an idea of their effectson the return waveform. For example, a model optical volume-scattering return is created using Equation (21), the sample distribution of n(h) in Figure 8 along with the ice layer at 1 m and the ground-truth values of σB. To get the total return power, P r, in Equation (24), this optical volume-scattering model is combined with a model surface return having typical values of 0.20 m and 4° for σ h, and s, resulting in the final model percolation-zone waveform in Figure 10a. As expected, the ice layer has the largest effect on the waveform, creating the second peak at 1 m from the surface. Figure 10b is an actual AAFE return waveform obtained from the Dye 2 area during the 1993 ground-truth experiment. This waveform exhibits a second peak similar to that in the model waveform in Figure 10a. The satellite altimeters do not typically observe these double-peak waveforms because the average depth of the ice layer varies over the much larger satellite footprint and therefore the ice-layer effect will not be as pronounced in the waveform.

Fig. 10. Altimeter model and actual returns from the percolation zone, (a) The combined surface and volume-scattering model and (b) actual AAFE return waveform from the percolation zone.
Both the model and actual waveforms agree with results from the ground-based Ku-band FMCW radar operated at Dye 2 during the 1993 ground-truth experiment. Nadir results for this radar show a significant return from the surface and from the ice layer at 1 m and smaller returns from the ice lenses and pipes (Reference Jezek, Gogineni and ShanablehJezek and others, 1994, Reference Zabel and JezekZabel and others, 1994; personal communication from I. Zabel, 1993). Therefore, when a continuous ice layer is present in the percolation zone, it is the dominant scatterer and has the greatest effect on the AAFE return waveform.
Although this model agrees with some of the altimeter returns from the percolation zone, it does not explain other more complex waveforms such as those in Figure 6. Since both n(h) and σ B(h) play an important role in the return waveform and both may vary significantly through the percolation zone, it is difficult to invert the relationship in Equation (21) and determine n(h) and σB(h) from an actual waveform. Equation (21) does, however, show the relationship between the return and n(h) and σB(h), and allow sample distributions to he inserted and manipulated to illustrate the effect on the return waveform.
C. Dry-Snow-Zone Model
In the dry-snow zone, where there is no summer melting, the density of the snow is low and the liquid-water content is 0%. Measured values of snow density, which lie between 0.28 and 0.38 Mg m−3 (Reference BensonBenson, 1962) result in attenuation coefficients less than 0.1 Np m−1 or l dB m−1 and depths of penetration greater than 5 m. Such a low attenuation coefficient suggests that a significant component of the return waveform is due to volume scattering from the sub-surface snow.
The scattering due to the sub-surface volume, P rv(t), again calculated using the volume-scattering radar-range equation (Reference Swift, Hayes, Herd, Jona and DelnoreSwift and others, 1985):

The individual snow grains, which are less than 0.5 mm in this region, are small relative to the 2.16 cm wavelength of the altimeter. Therefore, the volume scattering a primarily due to Rayleigh scattering (Reference Ulaby, Moore and FungUlaby and others, 1981). As a result, the volume-backscatter coefficient, η v, is
where σ B is the Rayleigh backscatter cross-section per particle and n is the density per unit volume. In the dry-snow zone, the density of the snowpack and the size of the snow grains are fairly constant in the upper several meters (Reference LingLing, 1985), resulting in an σ B and n that are constant with position. The resulting return power due to the Rayleigh volume scattering is

where

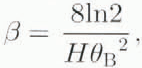
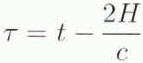
and
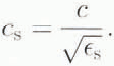
Equation (29) was obtained by performing the integral in Equation (27) in cylindrical coordinates. Reference Davis and MooreDavis and Moore (1993) obtained similar results by performing the analysis in spherical coordinates. Figure 11 shows how varying the attenuation coefficient, α, of the sub-surface snow affects the shape of the volume-scattering return. As α approaches infinity, the depth of penetration goes to zero and, as expected, the volume-scattering return goes to zero. On the other hand, as α goes to zero, the depth of penetration approaches infinity and Ρ rv(τ) becomes a function of the antenna beamwidth.

Fig. 11. Effects of varying attenuation, τ, on the Rayleigh volume-scattering model of the dry-snow zone of Greenland.
As in the percolation zone, the total return power, Ρ r(τ), is the incoherent sum of the surface- and volume-backscatter components. The series of waveforms in Figure 12 illustrates the effect of varying the attenuation coefficient on the total return power. This is done by changing the snow density and liquid-water content using Equation (1) and (2). The first waveform shows that a liquid-water content of 3% results in a return that is predominantly due to surface-scattering. Sub-surface scattering effects do not appear until the liquid-water content approarhes 0%. The following waveforms in Figure 12 illustrate the effect of keeping the liquid-water content at zero and reducing the snow density from 0.40 to 0.27 Mg m−3.

Fig. 12. Combined surface and Rayleigh volume-scattering model for varying values of snow density, ρs and liquid-water content, mv.
Values of the attenuation coefficient in the dry-snow zone are determined using an LMSE fit to a non-linear seven-parameter model, which is the sum of Equation (24) and a noise-floor parameter or
This combined surface and Rayleigh volume-scattering model explains a return waveform such as waveform 6 in Figure 1, which has a sharp leading edge and a long, gently sloping trailing edge. As Figure 13 shows, the combined model fit to waveform 6 yields σ h = 0.42m, s = 2.6°, α = 0.1 Np m–1 and δ p = 5.0 m, which are reasonable surface and sub-surface parameters for the dry-snow zone. Using the attenuation coefficients, α, and assuming the snow is dry and has m v = 0%, results in an approximate snow density of ρ s = 0.29 Mg m−3. Attenuation coefficients from a section of the dry-snow zone obtained by fitting the combined model in Equation (34) to AAFE return waveforms have an average of 0.11 Np m−1 or 1 dB m−1. This is equivalent to an approximate snow density of ρ s = 0.28 Mg m−3. Reference Davis and ZwallyDavis and Zwally (1993) fitted a similar combined surface- and volume-scattering model to GEOSAT radar-altimeter waveforms and obtained values between 0.1 and 0.l5 Np m−1 in the dry-snow zone at 72° N, which was die upper extent of the SEASAT satellite coverage.

Fig. 13. Combined surface and Rayleigh volume-scattering model fit to waveform 6 in Figure 1.
Figure 14a and b show values of σh, and s from the same fit to Equation (34). The values of σ h are similar to those shown in Figure 4b over this same flight section, which were obtained when the waveforms were fitted to the surface-scattering model of Equation (15). This shows that, although Rayleigh volume scattering affects returns from the dry-snow zone, a surface-scattering model can be used for rms surface-height measurements, since the leading edge of the waveform is always due to a surface return. Values of s, on the other hand, cannot be obtained using the surface-scattering model in the dry-snow zone. The combined model, however, allows part of the trailing edge to be attributed to s and part to α, resulting in reasonable values of rms surface slope, such as those shown in Figure 14b. This model, however, does not take into account slope-induced error and mispointing angle of the aircraft, and therefore some of the data points may be biased slightly higher than expected.

Fig. 14. Results of the combined surface and Rayleigh volume-scattering model fit to AAFE return waveforms from the dry-snow zone of the Greenland ice sheet, (a) Values of rms surface height, σh; (b) Values of rms surface slope, s.
3. Discussion and Concluding Remarks
As Figures 1 and 6 showed, the shape of the AAFE airborne-altimeter waveforms differs significantly from satellite returns from the Greenland ice sheet. One reason for this difference is the significantly smaller footprint of the airborne instrument The AAFE altimeter has a 15.6° 3 dB beamwidth and a 2.77 ns compressed pulse width and, as a result, when the aircraft altitude is 400 m, its pulse-limited footprint is less than 20 m and its beam-limited footprint is less than 125 m. A reflective surface that is rough enough to reflect power back to the radar even at the farthest extent of the beam-limited footprint will create an AAFE waveform that is approximately 30–40 range bins wide from the beginning of the leading edge to the end of the trailing edge. The SEASAT satellite radar altimeter had a similar pulse width of 3.2 ns, but its 1.6° beamwidth and 800 km orbit (Reference DavisDavis, 1992) result in pulse-limited and beam-limned footprint radii of greater than 875 m and 11 km, respectively. As a result, SEASAT returns from the same rough surface will create waveforms that are more than 100 range bins wide. The range-bin size of both systems is similar due to the equivalent pulse widths but this significant difference in the waveform width or length of the trailing edge makes the two returns appear very different.
Another cause for the differences between the airborne and satellite waveform shapes is the effects of rms surface slope, s, on the altimeter waveform. Figure 15a shows the effects of varying s on the AAFE return waveform for a constant altitude of 400 m. Once the rms surface slope approaches the same order of magnitude as the AAFE beamwidth, the waveform achieves its maximum width or the return is a full waveform. The occurrence of rms surface-slope values on the order of 15.6°, however, is very unlikely and therefore surface scattering alone cannot produce a full waveform for the AAFE altimeter. As Figure 15b shows, the SEASAT returns approach a maximum width or a full waveform when the rms surface slope exceeds 1.6°, but the AAFE returns will not be full until s exceeds 15.6°. Since the rms surface slope on the Greenland ice sheet is usually less than a few degrees, the effects of volume scattering on the trailing edge of the AAFE waveform are easy to see. The SEASAT satellite-altimeter returns, on the other hand, are typically full waveforms and the effects of volume scattering on the trailing edge are less evident.

Fig. 15. Comparison of airborne- and satellite-altimeter waveforms. Effects of varying rms surface slope on (a) the airborne-AAFE-altimeter return waueform (assuming a constant altitude of 400 m and a beamwidth of 15.6°); (b) the satellite-altimeter waveform (assuming a constant altitude of 800 km and a beamwidth of 1.6°).
A third cause of the differences in waveform shape is that the area of the satellite-altimeter footprint is over 2000 times greater than the AAFE airborne footprint. As a result, the deviation in surface altitude of the ice sheet across the satellite footprint can be much greater than across the airborne-altimeter footprint, causing a longer, more gently sloping trailing edge in the satellite-altimeter return. This also creates the double-ramp waveforms reported by Reference Martin, Zwally, Brenner and BindschadlerMartin and others (1983), which were not recorded with the airborne AAFE altimeter.
Despite the differences in the airborne and satellite waveforms, these models of the diagenetic zones of Greenland provide a better understanding of how the radar-altimeter Ku-band pulse interacts with the ice sheet. In addition, these models allow important geophysical parameters to be measured, such as rms surface roughness and slope in the ablation and soaked zones, and attenuation and depth of penetration in the dry-snow zone. Although the percolation zone is complex and difficult to model, the ground-truth data taken at Dye 2 have helped in modeling this area. The next step in understanding scattering in this region is to use a multiple-scattering model to explain the complex radar-altimeter waveforms that are often obtained in the percolation zone.
During the next few years, the NASA airborne group will repeat many of the original flight lines over Greenland. Comparisons between the 1991 and 1993 results and these future experiments will allow changes in the geophysical parameters of the ice sheet to be monitored.
Acknowledgements
The authors would like to thank the Observational Sciences Branch at the NASA Wallops Flight Facility, especially W. Krabill and E. Frederick for providing the GPS and AOL data and Dr R. Thomas for providing the funding for this project under NASA grant NGT-50606. They would also like to thank Dr C. Rowe and Dr M. Anderson from the University of Nebraska for their help in the probing experiment at Dye 2.


















