Introduction
Rise of sea level caused by increased discharge of ice from the world’s glaciers, ice caps and ice sheets would have numerous profound economic and social consequences (Reference Schneider, Parry, Canziani, Palutikof, van der Linden and HansonSchneider and others, 2007). The fate of land-based ice depends on future climate and dynamics of outlet glaciers terminating in the sea. Climate variations have immediate effects on the glacier surface, but effects on the overall behavior of outlet glaciers that are cumulative over decades or centuries are poorly understood.
Shrinkage of southeastern Alaska glaciers accounts for ∼20% of the total contribution of glaciers, ice caps and ice sheets to sea-level rise (Reference MeierMeier and others, 2007). Recent volume changes of several glaciers in the region (including Columbia Glacier) have been determined by laser altimetry (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002). Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) compared recent satellite imagery with earlier digital elevation models constructed by the US Geological Survey (USGS) and determined that mass loss of Columbia Glacier over ∼1960–2006 was ∼6% of the total loss of Alaska glaciers. These studies of mass loss do not separately resolve effects of surface mass balance and mass loss by calving.
The extensive observational record at Columbia Glacier, and previous analysis of it, is an invaluable resource for investigating the behavior of such ocean-terminating glaciers. The major part of this record is the series of 139 vertical aerial photography flights between 1957 and June 2010, most of which covered only the ∼20 km long lower reach. Photogrammetric analysis yielded changes between successive flights in horizontal and vertical coordinates of many identifiable surface features (Reference KrimmelKrimmel, 2001). As noted below, however, there is only a very small body of surface mass-balance measurements.
There is only a small record of 67 direct measurements of surface mass balance on Columbia Glacier in 1977–78 (Reference Mayo, Trabant, March and HaeberliMayo and others, 1979), 1983–95 (Reference KrimmelKrimmel, 2001) and 1992–97. A model of surface mass balance (Reference Rasmussen and ConwayRasmussen and Conway, 2004) using an established upper-air database is calibrated here for Columbia Glacier with the 67 measurements.
The model thus calibrated is used to construct the surface mass-balance record over 1948–2007. This paper also estimates the 1948–2007 iceberg production resulting from the combination of surface mass-balance processes and volume loss due to drawdown of the glacier surface, as well as disintegration of the part of the lower reach between the pre-retreat terminus and the 2007 terminus. Projecting possible future dynamic changes in the glacier is not the purpose of this paper. Future surface mass balance, however, is estimated under continuation of climate conditions that existed over 1995–2007 and under postulated changes in temperature and precipitation.
Columbia Glacier
Columbia Glacier (Fig. 1) is a large temperate glacier flowing from 3700 m a.s.l. on the south side of the Chugach Mountains to a fjord that empties into Prince William Sound. From its first recorded observation in 1794 (Reference VancouverVancouver, 1798) until ∼1981, the glacier terminus rested on a marine shoal at about L = 67 km, where L is the distance from the head of the glacier measured along its main flowline. At that time the glacier area was ∼1070 km2. Reference Calkin, Wiles and BarclayCalkin and others (2001) found that the advance to that position from at least 10 km up-glacier began as early as the 15th century.

Fig. 1. Columbia Glacier, showing pre-retreat and later terminus positions. Closed circles indicate 1977–78 mass-balance stake measurements. Crosses are crevasse measurements. Open circles indicate distance, L, (km) from the head of the glacier following the main flowline. Universal Transverse Mercator (UTM) coordinates (m) are in zone 6 of the North American Datum of 1927 (NAD27). Contours are for pre-retreat topography (fig. 1 of Reference Mayo, Trabant, March and HaeberliMayo and others, 1979). Valdez AP is at 61.3° N, 146.35° W. The nearest NCEP/NCAR point is at 60° N, 147.5° W.
Water depths at the shoal measured in 1973 ranged from <2 to ∼30 m, but behind it the water was several hundred meters deep (Reference PostPost, 1975). Post correctly surmised that if the terminus retreated into the deeper water, calving would increase beyond the rate of ice flow to the terminus, and the glacier would undergo drastic retreat. Terminus retreat began slowly in ∼1981 and accelerated to its maximum rate (∼1 km a−1) 10 years later (Reference KrimmelKrimmel, 2001). Although the rate of flow to the terminus increased by about an order of magnitude, it could not compensate for the increased calving (Reference Van der VeenVan der Veen, 1995). Ice speed at the terminus increased from ∼2 km a−1 in 1981 to ∼12 km a−1 in 2001 (Reference PfefferPfeffer, 2007).
By 2004 (Reference O’Neel, Pfeffer, Krimmel and MeierO’Neel and others, 2005) the terminus had retreated to L = 52 km and by 2010 to L = 49 km (Fig. 1). According to radar soundings in 1977 and 1978 (Reference Mayo, Trabant, March and HaeberliMayo and others, 1979), the glacier bed is below sea level for another 15 km up-glacier from the 2010 terminus position. Reference PfefferPfeffer (2007) concluded from analysis of the glacier’s flow characteristics that retreat will continue.
Data Sources
Surface mass balance
Surface mass-balance measurements were made in late summer 1977 and 1978 on the glacier (Reference Mayo, Trabant, March and HaeberliMayo and others, 1979) at 56 locations ranging from 135 to 2645 m a.s.l. They were made by the direct glaciological method of using stakes drilled into the ice. A few other measurements were made indirectly.
On 3 August 1997, D. Trabant and Krimmel measured on crevasse walls the depth from the glacier surface to the ash layer deposited by the 18 August 1992 eruption of Mount Spurr, 260 km to the west. Mean altitude of the sites over the 5 years was determined by taking into account glacier slope and 1992–93 measured flow, resulting in assigning a mean altitude 60 m above that measured in 1997. Mean altitudes of the ten sites range between 944 and 2498 m a.s.l.
Surface lowering was measured photogrammetrically on the occasion of ten vertical aerial photography flights (6 November 1983 to 27 September 1995) at a site on stagnant ice near the terminus (Reference KrimmelKrimmel, 2001). The rate of lowering was nearly constant over the 12 year period while the surface altitude at the site decreased from ∼200 to ∼100 m. Because the glacier surface there in that season is snow-free, the lowering is due to ice loss, about −9.4 m a−1.
Mass-balance records for Wolverine and Gulkana Glaciers were integrated over their 1966 topography (Reference Van Beusekom, O’Neel, March, Sass and CoxVan Beusekom and others, 2011) and for South Cascade Glacier over its 1970 topography (Reference RasmussenRasmussen, 2009). These USGS programs have been maintained since 1966 at the first two glaciers, and since 1958 at the third.
Glacier geometry
The 1957 area–altitude distribution in 100 ft (∼30.5 m) altitude bands was supplied by S. O’Neel (personal communication, 2009). The 2007 area–altitude distribution in 50 m altitude bands derived from 5 m resolution satellite images (Reference Korona, Berthier, Bernard, Rémy and ThouvenotKorona and others, 2009) was supplied by E. Berthier (personal communication, 2010).
Bathymetry of part of the fjord occupied by the glacier prior to retreat was surveyed by the US National Oceanographic and Atmospheric Administration (NOAA) in September 2005. It was supplied south of L = 51.7 km (Fig. 1) on a 100 m square grid by S. O’Neel (personal communication, 2009). Bathymetry on a 200 m square grid south of L = 55.3 km was constructed (Reference KrimmelKrimmel, 2001) from surveys by the USGS in late summer or fall over 1995–97. Calving rate over 1981–95 is also given by Reference KrimmelKrimmel (2001).
Meteorological conditions
US National Centers for Environmental Prediction and US National Center for Atmospheric Research (NCEP/NCAR) Reanalysis data (Reference KalnayKalnay and others, 1996; Reference KistlerKistler and others, 2001) give values of meteorological variables at many levels in the atmosphere at integer multiples of 2.5° in both latitude and longitude. The database has the advantages that it has 6 hour temporal resolution, is free of missing values and is maintained as an integral part of an ongoing major scientific enterprise. The nearest gridpoint (60.0° N, 147.5° W) is 125 km due south of the 2007 glacier terminus. Daily data there at 1200 UTC for 1948–2007 at four standard levels, 1000, 925, 850 and 700 hPa, were downloaded in May 2008 from Columbia University: http://ingrid.ldgo.columbia.edu/SOURCES/.NOAA/.NCEP-NCAR/.CDAS-1/.
Daily meteorological observations have been made since summer 1975 at the Valdez US National Weather Service Office (61.13° N, 146.35° W), which is ∼35 km east of the 2007 glacier terminus. Seasonal variation of mean 1948– 2007 upper-air conditions is shown in Figure 2, along with mean 1976–2007 Valdez precipitation.

Fig. 2. (a–e) Mean 1948–2007 conditions at 850 hPa at 60° N, 147.5° W: (a) geopotential height, (b) temperature, (c) relative humidity, (d) wind speed (upper) and magnitude of mean vector wind (lower), and (e) direction of mean vector wind. (f) Mean 1976–2007 Valdez precipitation.
Surface Mass-Balance Model
Mass-balance modeling has historically obtained meteorological data either from regular weather service stations for analysis over several years (Reference De Woul and HockDe Woul and Hock, 2005) or from automated weather stations operated on or near the glacier for analysis over one or a few years (Reference Andreassen and OerlemansAndreassen and Oerlemans, 2009). Upper-air meteorological data were initially used to model surface accumulation by Reference Rasmussen and ConwayRasmussen and Conway (2001) and to model surface ablation by Reference Rasmussen and ConwayRasmussen and Conway (2003). They have been used since then to model mass balance in Scandinavia (Reference Rasmussen and ConwayRasmussen and Conway, 2005), Iceland (Reference RasmussenRasmussen, 2005), Svalbard (Reference Rasmussen and KohlerRasmussen and Kohler, 2007) and on Mount Rainier, Washington, USA (Reference Rasmussen and WengerRasmussen and Wenger, 2009).
Surface accumulation
Precipitation, P, is partitioned between rain and snow, c sfc, at any altitude, z, by interpolating temperature, T(z), in the NCEP/NCAR data. Rain, the part of P when T(z) > +2°C, is assumed to run off without refreezing in the glacier. Although other values have been used for the rain/snow transition, including 0°C by some authors, there is abundant support for using +2°C (Reference OerlemansOerlemans, 1991; Reference Førland and Hanssen-BauerFørland and Hanssen-Bauer, 2003; Reference Kohler and AanesKohler and Aanes, 2004).
Surface accumulation over the period [t 1, t 2] in days is taken to be equal to the snowfall, which is calculated from03C6

in which the flux, f, is

and pseudo-precipitation P = max[0, RH U(ϕ’)]. Here 0 ≤ RH ≤ 1 is the 850 hPa relative humidity and U is the component of the wind from critical direction ϕ’. That is
![]() , in which
, in which
![]() is the speed and ϕ
850 the direction of the 850 hPa wind. Because RH is dimensionless, f has the same units as U (m s−1). The proportionality coefficient, α, and critical direction, ϕ’, are two of the three parameters of the model.
is the speed and ϕ
850 the direction of the 850 hPa wind. Because RH is dimensionless, f has the same units as U (m s−1). The proportionality coefficient, α, and critical direction, ϕ’, are two of the three parameters of the model.
Mean 1948–2007 seasonal variation of calculated climatological conditions is shown in Figure 3 for 500 and 1000 m a.s.l. The snow fraction, c sfc/P, at 1000 m is uniformly high from mid-fall through late spring. At 500 m the fraction slowly increases from a low value early in that period and approaches the 1000 m value only at the end of it, even though T is comparable at the beginning and end. The cause is a peculiarity of the T(t, z) distribution: there are relatively more days with T ≥ +2°C at 500 m early in the winter than late, but not at 1000 m.

Fig. 3. Model estimates of climatological conditions averaged over 1948–2007. (a) Precipitation, (b) snowfall, (c) snowfall/precipitation ratio and (d) temperature. Heavy curves are for 1000 m a.s.l.; light curves are for 500 m a.s.l.
Model precipitation has about the same general seasonal variation as measured precipitation (Fig. 2) at Valdez, i.e. with a spring minimum, but has much greater amplitude. This is due in part to Valdez station being at the head of the fjord (Port Valdez; Fig. 1) and thus being partially shielded, by high topography, from storms from the south.
Surface ablation
A one-coefficient degree-day model is used to estimate ablation:

in which T + = max(0, T) and t 1 and t 2 are as in Equation (1). Temperature, T, is interpolated at z in the reanalysis data, and β is the third model parameter, along with α and ϕ’ in Equations (1) and (2).
The mean 1948–2007 June–September vertical profile of the T
+ sum is shown in Figure 4, along with that of
![]() .
.

Fig. 4. Mean June–September vertical profiles of temperature at 60.0° N, 147.5° W over 1948–2007. (a)
![]() (heavy) and
(heavy) and
![]() (light); (b) positive degree-days (PDD) ∑ T
+. Mean summer altitudes of the 1000, 925, 850 and 700 hPa levels are shown; in winter they are lower, from ∼50% at 1000 hPa to ∼10% at 700 hPa.
(light); (b) positive degree-days (PDD) ∑ T
+. Mean summer altitudes of the 1000, 925, 850 and 700 hPa levels are shown; in winter they are lower, from ∼50% at 1000 hPa to ∼10% at 700 hPa.
Annual surface balance
Surface mass balance is the sum of surface accumulation and surface ablation:
in which c sfc is given by Equations (1) and (2) and a sfc by Equation (3). Because the surface mass-balance measurements span such a large altitude range, there is good resolution of the coefficients α and β. Observations at high (low) altitude pertain mainly to the α (β) term. Conversely, if the measurements had all been at similar altitudes, the resolution would have been poor; i.e. Equation (4) would approach being one equation with two unknowns, α and β. That is, an infinite number of c sfc, a sfc pairs, and underlying α,β pairs, would satisfy Equation (4).
Temperature in the upper-air database is at 1200 UTC (about 0200 local time), which means T
+ is taken from near the minimum of the diurnal cycle. Thus coefficient β is numerically larger than it would be were T
+ taken near the maximum of the cycle. That is, β and the T
+ sum are inversely related because their product (Equation (3)) is controlled by the measured surface balance,
![]() , at low altitude. Amplitude of the diurnal cycle is small in the upper air, so this effect is probably also small.
, at low altitude. Amplitude of the diurnal cycle is small in the upper air, so this effect is probably also small.
Model results
Coefficients optimized by minimizing the root-mean-square (rms) error between measured and modeled values using the 67 mass-balance measurements over 1977–97 are α = 0.0061 s and β = 0.0041 m d−1 °C−1 with ϕ’ = 200°. The β value is typical for a snow-covered surface, which is the case on Columbia Glacier for much of the year. In comparing the model results with measurements, t 1 and t 2 in Equations (1) and (3) are the dates of the measurements. In calculating balances over other periods, t 1 and t 2 are chosen to span the entire year. Results are weakly sensitive to model parameter ϕ’ because of the slow variation of the cosine factor in the expression for U in forming P in Equation (2).
Goodness of fit of the model is expressed by the rms of the model errors,
![]() , and by the coefficient of determination (Reference BevingtonBevington, 1969):
, and by the coefficient of determination (Reference BevingtonBevington, 1969):
in which σ is the standard deviation of
![]() (z). The rms model error over the 67 cases is 1.0 m w.e. a−1 with r
2 = 0.88 (Fig. 5)
(z). The rms model error over the 67 cases is 1.0 m w.e. a−1 with r
2 = 0.88 (Fig. 5)

Fig. 5. Surface mass balance: measured (
![]() ) and model (b
sfc) estimates (n = 67). (Details are given in the Data sources section.)
) and model (b
sfc) estimates (n = 67). (Details are given in the Data sources section.)
Inclusion of a constant term in Equation (4) produces negligible improvement. Although the model makes the unusual assumptions that neither precipitation, P (Equation (2)), nor the degree-day coefficient, β (Equation (3)), varies with altitude, model error is uncorrelated with altitude (r = +0.05). Because there is no constant term in Equation (4), the mean error is not necessarily zero; in the results here it is +0.03 m w.e. Mean 1948–2007 vertical profiles of calculated surface accumulation, c sfc, surface ablation, a sfc, and surface mass balance, b sfc, are shown in Figure 6.

Fig. 6. Altitude variation of mean 1948–2007 surface mass-balance components.
An implicit assumption of the model is that surface mass-balance components do not vary along an altitude contour. The measurements vary principally with altitude but there is a slight secondary variation, such as in the annual values at ∼500 m (Fig. 5). Inability to capture lateral variation is a source of much model error. When integrated over the topography, however, much of this error component cancels out. Although the error is large at any particular site (1.0 m w.e. a−1), errors,
![]() , at individual sites tend to cancel each other when averaged over the entire glacier, for which 0.3 m w.e. a−1 is assumed. If uncertainty in stake measurements is the same order, and if the two sources are mutually uncorrelated, they combine to 0.4 m w.e. a−1.
, at individual sites tend to cancel each other when averaged over the entire glacier, for which 0.3 m w.e. a−1 is assumed. If uncertainty in stake measurements is the same order, and if the two sources are mutually uncorrelated, they combine to 0.4 m w.e. a−1.
Reconstructed surface mass balance, b sfc(z), over 1948–2007 at 1000 m a.s.l. (Fig. 7) has three distinct periods: before, during and after 1970–94. Mean annual balances were +0.18, +0.92 and −0.86 m w.e. in the three periods (Table 1). Compared with the middle period, the first and third were much drier, and the three periods were progressively warmer in winter, with a decreasing fraction of precipitation falling as snow. The role of Figure 7 is to separate effects of changing climate conditions from effects of changing glacier geometry. With surface lowering, for instance, the strong vertical gradients of the three components of surface mass balance (Fig. 6) would cause it to become more negative even if climate were unchanging.

Fig. 7. Mean 1948–2007 October–September surface mass-balance model results (m w.e. a−1) at 1000 m a.s.l. Each series is fit with a piecewise-constant function, stages of which are determined empirically, so the probability, p{t}, is small, according to the t test, that the values in two successive stages are from the same population. For all pairs of successive stages, p{t} < 0.01.
Table 1. Mean glacier-wide surface mass-balance components at 1000 ma.s.l. over principal subperiods (Fig. 7) calculated with Φ′ = 200°, α = 0.0061 s and β = −0.0041 m w.e. d−1 °C−1

Over June–September at 1000 m a.s.l., 1964–92 was 0.9°C cooler than either the previous or following period. These shifts correspond roughly with rises in North Pacific sea-surface temperature, in winter after 1976 and in summer after 1988 (Reference Hare and MantuaHare and Mantua, 2000). The Pacific Decadal Oscillation index was strongly negative in the first period, strongly positive in the middle period and mildly positive in the third.
Seasonal evolution of mean 1948–2007 modeled cumulative surface mass balance is shown for 0, 500, 1000, 1500 and 2000 m a.s.l. in Figure 8. The curves for higher altitudes nearly coincide for the first ∼200 days of the season because precipitation is assumed to be constant with altitude, and above ∼1500 ma.s.l. temperatures are predominantly <+2°C.

Fig. 8. Mean 1948–2007 seasonal evolution of cumulative surface mass-balance model results relative to 1 October at 0, 500, 1000, 1500, 2000 and 2500 m a.s.l.
Sensitivity of model results to temperature shows that surface ablation at 1000 m a.s.l. would increase by 0.8 m w.e. a−1 under 1°C warming. In addition, change in the rain/snow partitioning would cause surface accumulation to decrease by 0.3 m w.e. a−1 for a total decrease of surface mass balance of 1.1 m w.e. a−1. Under an independent 10% increase in precipitation, surface accumulation would increase by 0.42 m w.e. a−1 . The effect of possibly increased cloudiness accompanying the increased precipitation on received solar radiation, and hence on surface ablation, is not considered.
Reference Lemke and SolomonLemke and others (2007) project that by 2100 temperature in the region will increase 3.2°C and precipitation by 21%, which have countervailing effects on surface balance. Combining sensitivities and projections yields changes by 2100 in surface accumulation of −0.1 m w.e.a−1, in surface ablation of −2.6 m w.e. a−1 and in balance of −2.7 m w.e. a−1 . Sensitivities and projections are expressed here using the index altitude 1000 m a.s.l. to separate climate effects from possible effects of changing glacier geometry.
Glacier-wide balances
The integral of surface mass balance over the area–altitude distribution (AAD) (Fig. 9) is approximated by

in which δA(zi ) is the glacier area in the altitude interval [zi − 25 m, zi + 25 m]. The 1957 AAD serves as a useful reference topography, as discussed by Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others (2001), which is relevant for climate investigations. Integrating over the evolving AAD, by contrast, combines the effects of climate variation and topography variation, which is relevant to investigation of total iceberg production.

Fig. 9. Area–altitude distributions with δA(z) in km2 per 50 m altitude increments. In 1957 the total area was 1068 km2 and the mean altitude was 1246 m; in 2007 they were 973 km2 and 1232 m.
Instead of explicitly obtaining intermediate AAD between 1957 and 2007, B
sfc(t) is approximated by interpolating linearly between
![]() in proportion to the variation of volume, V(t), relative to the 2007 volume:
in proportion to the variation of volume, V(t), relative to the 2007 volume:
In the absence of detailed information on the evolution of the topography, the zero-order assumption is made that change in AAD follows change in volume.
The integral over the 1957 AAD exceeds that over the 2007 AAD by ∼0.4 km3 in heavy surface accumulation years and by ∼0.1 km3 in light accumulation years. That is, high accumulation years favored
![]() more than
more than
![]() . Correlation of the difference with accumulation is r = +0.54, but with surface ablation it is negligible. Variation of B
sfc(t) integrated over the evolving AAD is shown in Figure 10. The generally positive surface mass balance from 1948 to 1995 was caused primarily by high surface accumulation over that period (Fig. 7).
. Correlation of the difference with accumulation is r = +0.54, but with surface ablation it is negligible. Variation of B
sfc(t) integrated over the evolving AAD is shown in Figure 10. The generally positive surface mass balance from 1948 to 1995 was caused primarily by high surface accumulation over that period (Fig. 7).

Fig. 10. Annual surface mass-balance model results integrated over evolving topography. Piecewise-constant function as in Figure 7, with p{ t} ≤ 0.01 for all pairs of successive stages.
Comparison with other glaciers
There are three glaciers in the region where the USGS has maintained surface mass-balance programs: Wolverine (60.4° N, 148.9° W, since 1966); Gulkana (63.3° N, 145.4° W, since 1966) and South Cascade (48.4° N, 121.1° W, since 1959). Critical direction, ϕ, assumed by the surface accumulation component, c sfc, of the model (Equations (1) and (2)), for Wolverine Glacier is 122° and for Gulkana Glacier is 238° (Reference Rasmussen and ConwayRasmussen and Conway, 2004), compared with 200° for Columbia Glacier.
Calculated glacier-wide annual surface accumulation, C sfc, at Columbia Glacier (Equations (1) and (6)) correlated with glacier-wide winter balance, B w, positively at Wolverine Glacier (r = +0.37), but negligibly at South Cascade and Gulkana Glaciers. Calculated glacier-wide annual surface ablation, A sfc, (Equations (3) and (6)) correlated strongly with glacier-wide summer balance, B s, at Wolverine (+0.80) and Gulkana (+0.76) Glaciers, but negligibly at South Cascade Glacier. Reference-surface balances (Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others, 2001) are used for all glaciers to take out the effects of changing glacier geometry.
Volume Change and Iceberg Production
Glacier volume change
Glacier topography is summarized concisely by its area–altitude distribution, shown in Figure 9 for 1957 and 2007. Change of glacier volume above sea level, ΔV + = −131 km3, over 1957–2007 is calculated geodetically using the two AADs. For comparison, E. Berthier (personal communication, 2010) estimated a loss of volume above sea level of 136 ± 5 km3. Dynamic thinning and disintegration of the lower reach between the pre-retreat position of the terminus, L = 67 km, and its 2007 position, L = 50 km, (Fig. 1) has been the major source of icebergs.
Effects of tectonic uplift are neglected. Reference PlafkerPlafker (1969) analyzed changes after the 27 March 1964 magnitude 8.4 earthquake with epicenter 61.06° N, 147.44° W. Although changes in the region varied from −2.5 to +11.5 m, they were negligible at Columbia Glacier and were −0.3 m at Valdez.
Changes in the mass of firn are also neglected by assuming Sorge’s law (Reference BaderBader, 1954). This holds that the density profile from the surface to the firn/ice transition is unchanging, so the entire thickness change in the ice/firn/snow column is due to change in the thickness of the ice. Since rapid retreat began, the total thickness has changed by hundreds of meters (Reference Walter, O’Neel, McNamara, Pfeffer, Bassis and FrickerWalter and others, 2010), so the possible changes in the firn thickness are comparatively small.
On the assumption that glacier topography changed little between 1948 and 1957, the total 1948–2007 volume change is taken to be the same as the total 1957–2007 change. When the USGS began ground observations in the mid-1970s, the basin seemed to be full of ice; i.e. ice levels from the terminus to the equilibrium line were abutting, but not encroaching into, mature heather and other plants growing in several inches of soil. This and old photographs by E.H. Harriman and W.O. Field (Reference BrownBrown, 2004) suggest that the glacier had been stable for several decades prior to then.
Estimating 1948–2007 change of glacier volume below sea level, ΔV− , is less certain. A bathymetric survey conducted by the NOAA in September 2005 sounded the full width of the fjord that had been previously occupied by the glacier as far north as L = 57.4 km (Fig. 1), yielding a volume of 10.6 km3. Between there and L = 52.1 km, the northern extent of the survey, floating ice prevented sounding the full width of the fjord. At each L value, on each side of the fjord, linear extrapolation from the last depth sounded to zero at the margin of the fjord yields an additional volume of 0.3 km3.
Maximum depth from the 2005 survey along an east–west line at each distance, L, from the head of the glacier is shown in Figure 11, along with the terminus-retreat history from figure 14 of Reference KrimmelKrimmel (2001). The volume between L = 52.1 km and the 2007 terminus, L = 50 km, is roughly estimated as an additional ∼2 km3. In sum, these yield ΔV− ≈ −13 km3. When combined with the value ΔV + = −131 km3, the total volume change is ΔV ≈ −144 km3.
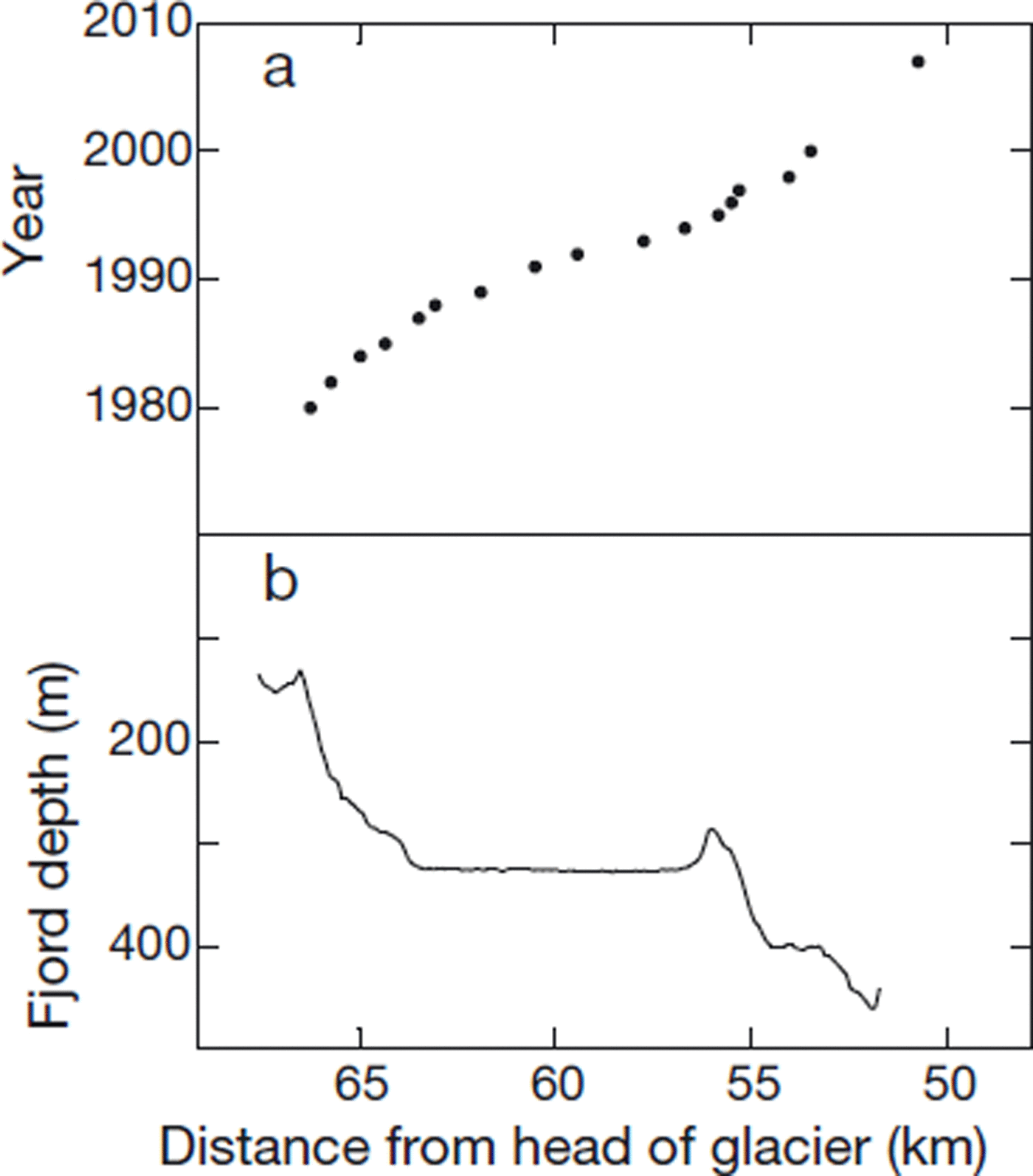
Fig. 11. (a) Terminus-retreat history (Reference KrimmelKrimmel, 2001) and (b) maximum depth in 2005 bathymetric survey along east–west line at each distance, L, from head of the glacier.
Comparison of the 2005 bathymetry with soundings made in the mid-1990s (Reference KrimmelKrimmel, 2001) showed that the 2005 depths were ∼7 m shallower over the section of the fjord between L = 55 and 67 km. In the case of erosion, Reference Motyka, Truffer, Kruiger and BuckiMotyka and others (2006) found during advance of Taku Glacier, Alaska, that rates averaged 4 m a−1 over 1989–2003. Uncertainty in the possible changes in the fjord bed is much smaller than the mean depth, which is ∼300 m.
There are three principal sources of uncertainty in the 1948–2007 volume change, ΔV. The largest is that in the change above sea level, ΔV +, for which Berthier’s 5 km3 is assumed. Next largest is that in the −13 km3 change below sea level, ΔV− , calculated from the 2005 NOAA bathymetry, which is assumed to be 2 km3. Third is possible change in the bathymetry due to sediment transport between the onset of retreat and 2005, for which 1 km3 is assumed. On the further assumption that these three are mutually uncorrelated, the resultant uncertainty is 5.5 km3.
Total iceberg production
Where ΔV is the change of volume, ∑ B sfc the sum of annual B sfc(t) and ∑ D the sum of annual calving volumes over any period of years, the three quantities are related through
Observations discussed above indicate that the glacier volume changed little from 1948 to 1981, but decreased ∼144 km3 from 1981 to 2007. That is, the amount, V(t), by which the volume exceeded the 2007 volume was ∼144 km3 from 1948 to 1981. Annual B sfc(t) summed over the 15 years from 1981 to 1995 (Equation (6)) gives ∑ B sfc = 18 km3 ice eq. Reference KrimmelKrimmel (2001, fig. 20) shows that over 1981–95 the calving flux, dD/dt, increased roughly linearly from ∼1.5 km3 a−1 in 1981 to ∼7 km3 a−1 in 1995; total calving volume, ∑ D, over that period was 60 km3.
Evolution of the volume thus assumed is shown in Figure 12, along with a piecewise-linear calving rate, dD(t)/dt, consistent with it and with the 1981–95 variation of Reference KrimmelKrimmel (2001); over 1995–2007 dD(t)/dt varied linearly from 7 km3 a−1 in 1995 to 9 km3 a−1 in 2007. Values of ΔV, ∑ B sfc and ∑ D are shown in Table 2 for each of the three subperiods. The 1948–2007 ∑ B sfc is 42 km3 ice eq., which combined with the ∼144 km volume loss yields a total iceberg volume of ∼186 km3. The cause of the difference in slope of dD(t)/dt between 1981–95 and 1995–2007 (Fig. 12) is that ∑ B sfc over the first subperiod is +18 km3 ice eq. and over the second is −6 km3 ice eq. That is, over the first subperiod ∑ B sfc > 0 augmented ΔV < 0 in producing ∑ D (Equation (8)), whereas in the second subperiod part of the ΔV < 0 was caused by ∑ B sfc < 0. About 64% of the decline in ∑ B sfc between the two subperiods was due to reduced surface accumulation, caused by both warming and drying, and the rest was due to increased surface ablation.

Fig. 12. (a) Evolution of volume, V(t), relative to 2007 and (b) piecewise-linear calving rate, dD(t)/dt, consistent with it and with the 1981–95 variation of Reference KrimmelKrimmel (2001). Over 1948–81, dD(t)/dt is shown as a uniform value integrating to ∑ D = ∑ B sfc over that period (Table 2).
Table 2. Variation of volume, V, annual surface mass balance, B sfc, surface accumulation, C sfc, surface ablation, A sfc, and calving, D, over principal periods of glacier change (Equation (8))

From 1948 until drastic retreat began, ∼1981, when volume change of the glacier was small, almost all iceberg production (30 km3) was from positive surface mass balance (Fig. 13). More detailed analysis of changes in calving is not possible because of uncertainties in the evolution of the volume of the glacier. Moreover, without using an advanced dynamic model it is not possible to determine the trajectories down to the calving front of changes in surface mass balance over the extent of the glacier.

Fig. 13. Decadal variation of components of volume change. Upper striped bar: glacier-wide surface accumulation; open bar: glacier-wide surface ablation; lower striped bar: calving; upper horizontal line: net glacier-wide surface mass balance; lower horizontal line: total volume change. Because of lack of detailed information on the evolution, V(t), of the volume of the glacier, the calving rate, dD/dt, is not strictly constant over 1948–81 but averages the same value as in Figure 12 (0.9 km3 a−1), so that volume change then is nearly zero.
Surface mass balance during the 1960s, for example, was slightly positive (Fig. 10). From continuity (Equation (8)), calving over that decade would also have been small, unless the glacier volume was decreasing. In addition, observations during the 1970s by Reference MeierMeier and others (1978) indicated up to 10 m a−1 of localized thinning near the terminus and increased iceberg discharge. During retreat, from 1981 to 2007, surface mass balance (12 km3 ice eq.) contributed only 8% of the total iceberg production (156 km3). The remainder was from dynamic thinning and disintegration of the part of the lower reach between the pre-retreat terminus and the 2007 terminus.
Discussion
Use of upper-air meteorological data in the NCEP/NCAR Reanalysis database has several advantages over using data from weather service stations or from instruments installed on or near the glacier. The temporal resolution and continuity of the record since 1948 make it a valuable resource for surface mass-balance modeling. The model described here can therefore compute surface mass balance over any time interval at any altitude.
The model adopts two simplifications that differ from assumptions usually made in mass-balance modeling, but that are justified by results here. One is that precipitation is constant with altitude. At Columbia Glacier, altitude increases generally to the north, away from the coast, which is in the downwind direction during precipitation events. Whereas precipitation might increase with altitude locally, it also decreases with distance from the coast, along the maritime/continental gradient in the region. Surface accumulation in the model does increase with altitude, even though precipitation does not because temperature decreases with altitude, so the fraction of precipitation falling as snow increases.
Another atypical model result is that the degree-day factor, β, can be constant with altitude. Its value is typical of values found in numerous PDD models for surface ablation on other glaciers (e.g. Reference Braithwaite and ZhangBraithwaite and Zhang, 2000; Reference HockHock, 2003), although in those models a larger value is used for exposed ice than for a snow-covered surface. The lower-albedo ice surface is exposed for a longer summer period at low altitude than at high, thus enhancing absorption of solar radiation over the season. Another condition at some glaciers is that their lower reaches are shaded for part of the day by nearby topography whereas the higher reaches are not. Because Columbia Glacier is large with little nearby strong relief except to the north, this effect is small there.
Although both simplifications would seem to contribute to negative model bias at higher altitude (underestimating surface accumulation and overestimating the magnitude of surface ablation) and the opposite bias at lower altitude, they are justified by the fact that model error,
![]() , is uncorrelated with altitude (r = +0.05). Much model error comes from the assumption that mass-balance components do not vary along an altitude contour. Measurements vary principally with altitude but there is a slight secondary variation, such as in the values at ∼500 m (Fig. 5). The model’s inability to capture any lateral variation is a source of much of its error, but failing to capture variation with altitude is not.
, is uncorrelated with altitude (r = +0.05). Much model error comes from the assumption that mass-balance components do not vary along an altitude contour. Measurements vary principally with altitude but there is a slight secondary variation, such as in the values at ∼500 m (Fig. 5). The model’s inability to capture any lateral variation is a source of much of its error, but failing to capture variation with altitude is not.
In this work we cannot speculate on future dynamic behavior of the glacier, but results do provide a basis for estimating thinning due to surface mass-balance processes. The approximately −0.5 km3 ice eq. a−1 surface mass balance over 1995–2007 (Fig. 10) when distributed across the ∼970 km2 area of the glacier averages ∼0.5 m a−1 thinning. Finer temporal resolution of the volume change and calving rate requires more advanced dynamic models (e.g. Reference PfefferPfeffer, 2007; Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others, 2010).
The finding that the retreat phase of Columbia Glacier proceeds independently of climate is not new (Reference ClarkeClarke, 1987; Reference Meier and PostMeier and Post, 1987; Reference O’Neel, Pfeffer, Krimmel and MeierO’Neel and others, 2005; Reference PfefferPfeffer, 2007). Such fast dynamic behavior is not restricted to tidewater glaciers of Alaska but is also a feature of outlet glaciers in Antarctica (Reference RignotRignot and others, 2008) and Greenland (Reference Howat, Joughin and ScambosHowat and others, 2007; Reference Joughin, Smith, Howat, Scambos and MoonJoughin and others, 2010). Additional studies are needed to quantify the processes and timescales that control the dynamic responses, and also to assess fluxes of surface mass balance and calving at other tidewater glacier systems.
Conclusions
Models of surface mass balance together with volume-change calculations are needed to determine the total volume of iceberg discharge from tidewater glaciers. Prior to retreat of Columbia Glacier, positive surface mass balance was offset by an equal amount of iceberg production (30 km3), an inference that was a direct consequence of assuming that the glacier volume was unchanging then. Calving then was only about a quarter of surface ablation (i.e. ∼4 km3 ice eq. a−1) and changed little over 1948–2007.
Between 1981 and 2007 the glacier experienced a period of accelerating volume decrease, mainly due to an increasing rate of iceberg production. During the first half of the retreat (1982–95), 4.3 km3 a−1 of ice was lost due to iceberg calving. This loss was partly offset by a 1.3 km3 a−1 gain in volume from positive surface mass balance over this period. In the later part of the retreat (1996–2007), 8.0 km3 a−1 of ice was lost by iceberg calving, with an additional 0.5 km3 a−1 of ice loss due to negative surface mass balance. Over 1948–81, calving was due entirely to positive surface mass balance, whereas since then only 8% has been, 92% being due to volume loss of the glacier (Table 2).
Allocating 1948–2007 calving volume, ∑ D ≈ 186 km3, to sea-level rise depends on the timescale considered. Over the period since retreat began, the biggest part is due to change, ΔV + ≈ −131 km3, of the volume above sea level. Some of the ∑ B sfc ≈ 42 km3 iceeq. contribution from surface mass balance includes short-term recycling of water from the sea. Results (Table 2) indicate that the contribution to sea-level rise increased from ∼0.008 mm a−1 during 1982–95 to ∼0.023 mm a−1 during 1996–2007 (determined using 3.62 × 10° km2 as the area of the sea). The recent value is slightly more than 1% of the total present-day eustatic sea-level rise of ∼1.8 mm a−1 estimated by Reference MeierMeier and others (2007). Loss of volume below sea level, ΔV− ≈ −13 km3, did not contribute because it was already displacing sea water. Moreover, as a consequence of the density difference between ice and sea water, its melting would slightly lower sea level.
Acknowledgements
We thank S. O’Neel for supplying the 2005 bathymetric survey and the area–altitude distribution for 1957, E. Berthier for the 2007 distribution, R. March for securing the base map for Figure 1 and H. Greenberg for determining the 2007 terminus position. Comments by W.T. Pfeffer improved the scope and content of the paper. Thoughtful comments by two anonymous reviewers greatly improved the clarity of the paper and are deeply appreciated. This work was supported by US National Science Foundation grant ARC 0732739.

















