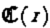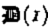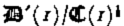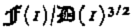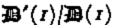1. Introduction
Undulations on the surface of ice sheets with a predominant wavelength of the order of several times the ice thickness have been studied by many authors in the past, notably by Reference BuddBudd (1970[a], Reference Budd[b], Reference Budd1971) who also gives an account of the relevant literature. For steady-state conditions he was able to relate the frequency spectrum of the bedrock topography to that of the surface and could explain, for instance, under what circumstances the basal shear stress fluctuates in sympathy with the surface slope. Budd considered the non-Newtonian viscous flow of a medium down a uniform slope with small harmonic undulations superimposed on it, but resorted to an approximate solution technique. A clear separation of the solution for bedrock undulations and steady-state accumulation-rate was not attempted, nor was there any systematic treatment of the transient response. Moreover, some of his boundary conditions were derived using an integrated mass-balance law, an unnecessary and doubtful procedure.
For these reasons, Hutter and others (in press) re-investigated the entire matter anew, first aiming at a clear and systematic formulation of the governing equations, secondly separating the steady-state and the transient response; and, thirdly, attempting to use a perturbation technique to answer various questions concerning the state of stress and velocity in a nearly parallel-sided slab. In this paper the analysis of Hutter and others is continued insofar as we investigate the time-dependent response. Our interest is, in particular, in the variation of the surface undulations as a result of initial disturbances and/or time-dependent accumulation rate. This must, under certain circumstances produce surface waves travelling down the glacier. Such waves were treated by Reference NyeNye (1960, Reference Nye1963[a], Reference Nye[b]) using kinematic wave theory. In that theory the ice slope is regarded as a whole. Balance of mass forms the only significant field equation, and balance of momentum is virtually abandoned, except, perhaps, as it enters the continuity equation through a phenomenological equation connecting discharge with depth and surface inclination.
Contrary to kinematic wave theory, the present approach makes full use of the momentum equation, in which, however, acceleration terms are discarded. The mathematical complexities introduced thereby are overcome by a stretching of coordinates. This restricts the disturbances to surface waves with wavelengths which are long compared to the mean thickness of the ice sheet, but short compared to its length; however, the method has the advantage that it delivers the wave speeds and the diffusivities as functions of the geometry of the ice slope and the boundary conditions at the ice-bedrock interface in a much more systematic way than is possible with the kinematic wave theory. Two features are new when compared with kinematic wave theory. First, the governing equation for the surface elevation depends on the ratio of ice thickness to a typical wavelength. Secondly, Glen's flow law must be generalized, because otherwise our proposed solution technique fails. The reason for this failure is natural, because in Glen's flow law stress deviators grow infinitely fast at low strain-rates, a singular behaviour that leads to singular integrals in the solutions.
2. Governing equations
Consider slow flow of a viscous medium of uniform thickness down a uniform slope. Let (x, y) be a Cartesian coordinate system; x is down and y normal to the plane. Further, let (u, v) be the components of the velocity vector v in the x- and y-directions respectively, and denote by
where t ij ′ is the stress deviator (the stress tensor will be denoted by t ij ) and t II′2 its second invariant, A is temperature dependent in general, but will henceforth be assumed constant; this is only a qualitative limitation which does not affect the essential conclusions of the calculations. B is an as yet unspecified function; for Glen's flow law B(x) ═ x (n − 1)/2.
In what follows it is advantageous to non-dimensionalize lengths, stresses, and time with the mean thickness of the undisturbed, strictly parallel-sided slab, D, σ0 ═ ρg D where ρ is the ice density and g the gravitational constant, and τ = A −1[ρgDB (ρ2 g 2 D 2]−1. Thus

For ice and Glen's flow law τ is in the order of 1 to 3 dFootnote *.
In non-dimensional variables, the governing field equations are:

where γ is The slope angle, and u, v are the dimensionless velocity components in the x and y directions, respectively, and

For ice obeying Glen's flow law,

in which ø is a constant whose value may substantially vary from glacier to glacier, and at the surface, i.e. at y = γ(x, t),

In these equations

The first of (Equations 5) is a non-linear sliding law accounting for a possible regelation mechanism. For ø = 0 it includes the no-slip condition. As a first approximation we have neglected a thorough treatment of bedrock undulations. Very roughly, they are incorporated in (Equations 5), however, and can be taken into account by adjusting ø accordingly.
A steady solution of (Equations 3), (5), and (6), henceforth denoted by a circumflex and valid for vanishing steady accumulation rate

Here a comment regarding the choice
Consider fluctuations on the motion given by (Equations 8); denote these by tildes so that u = û + ū. The governing equations can now be separated for the two parts. We shall perform this separation under the assumption that the steady-state stresses are large in comparison to the stresses set up by the transient motion. The perturbation equations can then be linearized with respect to the stresses so that the following perturbation equations are obtained:

in which and

In this paper we shall consider long surface waves; in other words, wavelengths of the time-dependent surface undulations will be assumed to be large in comparison to the mean glacier thickness. Needless to say the total length of the glacier is also assumed to be large :compared to these wavelengths. Based on this we introduce the stretchings

where μ may be interpreted as the ratio of the mean thickness to a characteristic wavelength. Incorporating (Equations 11) in (Equations 1) gives (deleting tildes)

In these equations quantities with a circumflex are known from the solution of the steady-state problem, and

at the top surface (y = γ(ξ, τ))

It is about at this point that we should comment on the introduction of the stretchings, (Equations 11). Time was stretched to balance all members on the left-hand side of the first of (Equations 14). Only in this case does it admit possible wave-like solutions. We shall see corroboration for this in the following section, because the emerging equation for surface elevation will essentially be a forward wave equation. The stretchings were further such that the kinematic boundary condition in (Equations 14) was preserved; this was not so with all other stretchings we tried. Incidentally it is well known in fluid mechanics (see, e.g. Reference StokerStoker, 1957; Reference BenneyBenney, 1966) and may, for instance, be used to derive the shallow-water equations. But what have we gained? The stretching parameter has explicitly entered the governing equations, and since it is small this suggests a perturbation solution technique which carries the advantage that surface-wave and velocity field have been mathematically decoupled: the solution of the former can be used in the determination of the latter. This will become clear below.
Our aim is to develop asymptotic solutions of the non-linear problem for μ small. The physical interest is in waves induced by the accumulation/ablation rate
We emphasize that (Equations 12)–(1) are for long waves of small amplitudes even though they are formally written for finite amplitudes. Solutions must therefore be sought in the form

These will be restricted to the steady-state results of (Equations 8), which themselves are based on (Equations 5) that neglect bedrock topography. Small undulations of the latter could be introduced by means of a second perturbation parameter. This will not be attempted in this paper.
3. On Glen's flow law
Despite its general acceptance in glaciology, Glen's flow law has its shortcomings. The most serious one is its singular behaviour at small stress deviators and strain-rates: for very small strain-rates the stresses grow infinitely fast. To avoid such pathological behaviour Glen's flow law can, for instance, be altered by introducing a polynomial law instead. This was suggested by Reference LliboutryLliboutry (1969). By simply fitting experimental data he obtained
where a, b, and c are temperature dependent at most. Unlike Glen's law, B(x) = X (n−1)/2, the constitutive relationship for the stress deviator based on Equation (16) no longer shows the singular behaviour at zero stresses.
There have been other proposals to change Glen's flow law. Reference Barnes, Barnes, Tabor and WalkerBarnes and others (1971) and Reference Ramseier and DickinsRamseier and Dickins (1972), for instance, suggest instead of Equation (16) a hyperbolic sine
where n and β are constants, but such a law still leads to infinite viscosities and thus does not remove the mathematical singularities mentioned above. For that purpose a finite-viscosity law must be developed. Reference Colbeck and EvansColbeck and Evans (1973) give a form similar to that of Lliboutry. On the other hand, using a model of statistical mechanics, in which rate-process theory is used, the law
where f (·) is a polynomial, can be derived (a paper on this is in preparation). A power-series expansion for small x reduces this to a polynomial similar to Equation (15).
For most computational purposes the odd behaviour of Glen's law does not matter. This paper is an exception, because the mathematical approach used here will become singular when based on a Glen-type power law. In order to avoid unnecessary complications, we shall, henceforth, use the simplest extension avoiding this singularity, namely
so that in view of the definition of

When introducing Equation (19) three constants, namely A,

Knowing these, a or
Before we present the solution technique a warning is in order which puts the mathematical approach into the proper perspectives. It is true that the difficulty with the use of Glen's flow law is a mathematical one connected to the proposed perturbation approach. (It has also arisen in finite-difference and other solution techniques of the respective equations, see Reference Hutter, Hutter, Legerer and SpringHutter and others (1979).) As
4. Long waves on an infinite ice slab
In this section we present the method of solution for the flow of a viscous medium of uniform thickness down a uniform slope. When the perturbation expansions (5) are substituted into (Equations 12)–(14) a hierarchy of initial-boundary-value problems is obtained. The zeroth-order equations are

subject to the boundary conditions

and

When using the generalized Glen's law of Equation (19) straightforward integration yields

where

There remains the determination of the surface topography. It may be derived from the third of (Equations 24) and the resulting (Equations 25). One obtains

with

Equation (27) is the desired result. For
which determines γ(ξ, τ) implicitly. The resulting Equation (29) implies that a given disturbance will deform with progressing time; the solution must eventually fail as the profile steepens and μ becomes finite.Footnote * The above results do not yet give indications on the unsuitably of Glen's flow law. Indeed we may set
The perturbation procedure outlined above yields a sequence of linear non-homogeneous differential equations subject to boundary conditions some of which are non-linear. The zeroth order approximation resulted in the forward-wave Equation (29). It can be improved by constructing higher-order approximations. To second order one then obtains

The functions
Analytical solutions to Equation (30) are probably hard to find, yet some insight can be gained for special cases. To this end let us write γ = 1 + δη) (since η no longer appears we may use this symbol with this new meaning). Then

Here, the parameter δ represents a typical surface elevation above the undisturbed level γ = 1. According to the perturbation procedure it cannot be larger than O(μ) but could be smaller. Furthermore, Equation (31) gives indications on the size of

To first order in δ we find

Nothing can be inferred about the size of the various coefficients involved. In particular they need not be O(1), because they follow from the integrations performed in the Appendix. The remaining simplifications therefore depend on the order of magnitude of the various terms considered.
-
(i) If
and δ = 0(μ) the leading terms are (34)
(34)
-
(ii) If
and δ = 0(μ 2) then (35)
(35)
-
(iii) If
the leading terms are (36)
(36)
Clarity about which of these equations should apply is obtained if the magnitude of the various coefficient functions is determined. First indications follow, if we assume no slip, ø = 0, and use Glen's flow law,

with
5. Solutions of the governing equations
When compared with the kinematic wave theory as presented by Nye, none of the above equations matches fully with his own which is

Here, C0, C0 ' = dC 0/dξ, D o, and D o' = dD 0/dξ, are known functions of ξ. Differences between (Equations 32) and (37) evolve because Equation (37) is valid for a slope of ice with variable thickness, whereas Equation (32) was derived for a slab of constant thickness, and, clearly, because Equation (32) contains O(μ 2) terms. For steep slopes their neglect is justified. Solutions for this case are of limited interest, but follow most easily if Equation (32) is subject to the Galilean transformation

We then obtain the heat equation,

with the general solution

in which η 0(ξ) is the initial disturbance.
When applying Equation (38) to the non-linear Equation (34) what obtains is the inhomogeneous Burger equation (see, e.g. Reference Leibowich and SeebassLeibowich and Seebass, 1974)

where

Construction of solutions to Equation (41) depends on the magnitude of κ. If κ is large, small perturbation solutions are suggested. If κ = O(1) and, more generally, for all κ, solutions are determined by utilizing the Hopf-Cole transformation

which reduces Equation (41) to the linear equation

For arbitrary accumulation-rate it must be integrated numerically. For impulsive accumulation-rate

it can, however, be treated exactly, because then Equation (43) reduces to the heat equation. Thus we can solve the initial-value problem to find

which provides the detailed structure of the wave for all time; â(X) is identical with the initial disturbance of the surface elevation above its mean.
If κ is small, multiple time scales are suggested, but these are not needed, because when solutions to Equation (41) are constructed by the regular perturbation expansion

no secular terms arise. What obtains is a sequence of heat equations

of which solutions again have the form of Equation (40) and will not be repeated here. If O(μ 2) terms are included in an exploitation of Equation (32) the solution may again be written in convolution form

where the Green's function

which for μ = 0 reduces to Equation (40). When
a perturbation solution is suggested. It boundaries are at lnfinity this yields a hierarchy of heat equations, namely, if

of which the solutions have again the form of Equation (40).
For any other more complicated equation, say (Equations 35) or (36) direct numerical methods must be suggested for their solution.
6. Discussion and conclusion
The calculations performed above remain rather theoretical and are of little help for real glaciological problems as long as no numerical values for the various coefficients of the surface-wave equation are available. Since our model treats surface waves on a plane parallel-sided slab, it will be of value for a glacier in the regions for from its head or its snout.
Several effects are built into the model:
-
(i) finite inclination of the ice slab,
-
(ii) sliding of the ice over its bed,
-
(iii) generalization of Glen's flow law.
It is interesting to see how these effects influence the coefficients in the basic governing equations. All these can be summarized in the equation

The first two terms on the left-hand side represent essentially the kinematic wave theory including diffusion. In the original coordinates ξ and τ the corresponding equation contains two constants,

and then find to first order in μ

For Glen's flow law and when the ice adheres to the bed it was shown that

Fig. 1.
-
(a) Surface-wave velocity
as a function of the inclination angle γ parameterized for n = 2, 3 and various values of in the generalized Glen flaw law. No slip of the glacier at the bed.
in the generalized Glen flaw law. No slip of the glacier at the bed.
-
(b) Same as Figure 1a, but for the case when sliding occurs. The sliding law is ub = øτm, and has been used for m = 2. The thick lines are for ub = 0.005, the thin lines for ub = 0.01.

Fig. 2.
-
(a) Diffusion parameter
as a function of the inclination angle γ parameterized for n = 2, 3 and for various values of in the generalized Glen flow law. No slip of the glacier at the bed.
in the generalized Glen flow law. No slip of the glacier at the bed.
-
(b) Same as Figure 2a, but for the case when sliding occurs. The sliding law is ub = øτm, m = 2.
Diffusion being significant we shall henceforth and irrespective of what value the wavelength parameter may have, use X and T as independent variables. With their use a possible extension of kinematic wave theory follows from numerical values of
In Figure 3 I have plotted the first of these parameters as a function of γ, parameterized for different values of

where η O is the thickness behind the shock. Generally it must be expected to be close to unity so that η O –1

Fig. 3.
-
(a)
as a function of the inclination angle γ parameterized for n = 2, 3 and various values of in the generalized Glen flow law. No slip of the glacier at the bed.
in the generalized Glen flow law. No slip of the glacier at the bed.
-
(b) Same as Figure 3a, but for the case when sliding occurs. The sliding law is ub = øτm, m = 2.
The significance of the coefficient ϵ in Equation (50) can be estimated from Figure 4. (Effects due to this term are usually attributed to dispersion.) Unlike the functions of the previous graphs, the value of

Fig. 4.
-
(a) Dispersion parameter
plotted against the inclination angle γ parameterized for n = 2, 3 values of . No slip of the glacier at the bed.
. No slip of the glacier at the bed.
-
(b) Same as Figure 4a, but for a sliding velocity ub, = 0.005. The sliding law is ub = øτm, m = 2.
-
(c) Same as Figure 4a, but for a sliding velocity ub = 0.01. The sliding law is ub = øτm, m = 2.
Finally, in order to obtain information about the magnitude of

Fig. 5.
-
(a)
plotted against the inclination angle γ for n = 2 and various values of a and several sliding conditions.
-
(b) Same as Figure 5a, but for n = 3.
In conclusion we may say that the surface-wave equation appropriate for ice slopes must have the form

where for ice I/ϵ is the dominant coefficient and where |ζ| is generally larger than |κ|, but smaller than unity. The non-linear terms in Equation (50) can safely be regarded as small corrections of the linear reduced equation, in which dispersion and diffusion are taken into account. The non-linear terms can safely be neglected so that the zeroth order equation reads

Of the diffusion and dispersion effects contained in this equation the second is more important than the former but this is a materially dependent property for which dependence on the parameter
Appendix
Here we briefly summarize the derivation of Equation (30). To this end the (Equations 12)–(14) are written for the o(μ) terms. The differential equations for the stresses are

and must satisfy the boundary conditions (see Equation (14))

and y = γ(x, t). Straightforward integration thus reveals

The longitudinal stresses

so that

It is now evident that a non-vanishing coefficient a prevents the first-order longitudinal stresses becoming infinite at η = 1. This demonstrates that the generalization of Glen's flow law is important.
To obtain the first-order velocity field the fifth and third of (Equations 12) must be integrated. From the former and the first of Equations (A.3) we obtain

Integrating this and using the boundary condition

gives as first-order longitudinal velocities

with

The first-order velocities


where

This completes the first-order solution; the results determine the wave Equation (20) as for as O(μ) terms go. To determine also the O(μ 2) terms, second-order shear stresses and velocities must be determined. The former follow from the first of (Equations 12), or

so that after an integration

is obtained, in which

The boundary condition for τ at η = γ implies that

Equations (A.10) and (A.12) together allow the determination of the constant of integration κ 1 (ξ, τ). Once it is determined, τ may be written in the form

in which

Beyond this point calculations are very involved. For this reason we shall restrict ourselves henceforth to the necessary minimum. Substituting (A. 13) and the fifth of (Equations 25) into the differential equation for

and using the boundary condition

it is straightforward to show that

Alternatively, the continuity equation

determines v as follows

with

These results now enable us to corroborate Equation (4.9). Indeed, with Equations (A.6), (A.7), (A.17), and (A. 18) the surface-wave equation, the first of (Equations 14), assumes the form of Equation (30), in which

Evaluation of the above functions hinges on explicit expressions for the functions

where