Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chin, William
and
Simson, Daniel
2010.
Coxeter transformation and inverses of Cartan matrices for coalgebras.
Journal of Algebra,
Vol. 324,
Issue. 9,
p.
2223.
Fu, Xuerong
Yao, Hailou
and
Hu, Yonggang
2023.
Triangular matrix coalgebras: Representation theory and recollement.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 02,

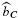 associated to
associated to 