Hostname: page-component-6d856f89d9-72csx Total loading time: 0 Render date: 2024-07-16T06:46:10.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Soliton-like solutions and chaotic motions for a forced and damped Zakharov–Kuznetsov equation in a magnetized electron–positron–ion plasma

Published online by Cambridge University Press:  29 July 2015

Hui-Ling Zhen ,
Bo Tian ,
De-Yin Liu ,
Lei Liu  and
Yan Jiang
Hui-Ling Zhen
Affiliation:
State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China
Bo Tian*
Affiliation:
State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China
De-Yin Liu
Affiliation:
State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China
Lei Liu
Affiliation:
State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China
Yan Jiang
Affiliation:
State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China
*
†Email address for correspondence: tian_bupt@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A forced and damped Zakharov–Kuznetsov equation for a magnetized electron–positron–ion plasma affected by an external force is studied in this paper. Via the Hirota method, the soliton-like solutions are given. The soliton’s amplitude gets enhanced with the phase velocity 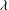${\it\lambda}$ decreasing or ion-to-electron density ratio 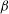${\it\beta}$ increasing. With the damped coefficient increasing, when the external force 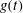$g(t)$ is periodic, the two solitons are always parallel during the propagation and background of the two solitons drops on the 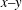$x{-}y$ plane, and amplitudes of the two solitons increase on the 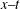$x{-}t$ and 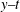$y{-}t$ planes, with 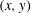$(x,y)$ as the coordinates of the propagation plane and $t$ as the time. 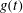When $g(t)$ is exponentially decreasing, the two solitons merge into a single one and the background rises on the 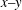$x{-}y$ plane, and amplitudes of the two solitons decrease on the 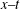$x{-}t$ and 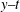$y{-}t$ planes. Further, associated chaotic motions are obtained when 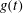$g(t)$ is periodic. Using the phase projections and Poincaré sections, we find that the chaotic motions can be weakened with 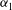${\it\alpha}_{1}$, the amplitude of 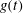$g(t)$, decreasing. With 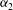${\it\alpha}_{2}$, the frequency of 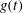$g(t)$, decreasing, a three-dimensional attractor with stretching-and-folding structure is found, indicating that the weak chaos is transformed into the developed chaos. Chaotic motions can also be weakened with 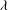${\it\lambda}$, the phase velocity, decreasing, but strengthened with ${\it\beta}$, the ion-to-electron density ratio, and 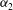${\it\alpha}_{2}$ decreasing.

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 5 , October 2015 , 905810515
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adnan, M., Williams, G., Qamar, A., Mahmood, S. & Kourakis, I. 2014 Pressure anisotropy effects on nonlinear electrostatic excitations in magnetized electron–positron–ion plasmas. Eur. Phys. J. D 68, 247–263.CrossRefGoogle Scholar
Ashraf, S., Yasmin, S. & Asaduzzaman, M. 2014 Electrostatic solitary structures in a magnetized nonextensive plasma with $q$ -distributed electrons. Plasma Phys. Rep. 40, 306–311.Google Scholar
Berezhiani, V. I., El-Ashry, M. Y. & Mofiz, U. A. 1994 Theory of strong-electromagnetic-wave propagation in an electron–positron–ion plasma. Phys. Rev. E 50, 448–452.Google Scholar
Berezhiani, V. I., Garuchava, D. P. & Shukla, P. K. 2007 Production of electron–positron pairs by intense laser pulses in an overdense plasma. Phys. Lett. A 360, 624–628.Google Scholar
Beiglböck, W., Eckmann, J. P., Grosse, H., Loss, M., Smirnov, S., Takhtajan, L. & Yngvason, J. 2000 Concepts and Results in Chaotic Dynamics. Springer.Google Scholar
Chen, H., Wilks, S. C. & Bonlie, J. D. 2009 Relativistic positron creation using ultraintense short pulse lasers. Phys. Rev. Lett. 102, 179501.Google Scholar
Dehghan, M. & Manafian, J. 2013 Analytical treatment of some partial differential equations arising in mathematical physics by using the exp-function method. Intl J. Mod. Phys. B 25, 2965–2981.CrossRefGoogle Scholar
Gao, Y. T. & Tian, B. 2006 Cosmic dust-ion-acoustic waves spherical modified Kadomtsev–Petviashvili model, and symbolic computation. Phys. Plasmas 13, 112901.Google Scholar
Glatt-Holtz, N., Temam, R. & Wang, C. 2014 Martingale and pathwise solutions to the stochastic Zakharov–Kuznetsov equation with multiplicative noise. J. Discrete Continuous Dyn. Syst. 19, 1047–1085.CrossRefGoogle Scholar
Hirota, R. 2004 The Direct Method in Soliton Theory. Cambridge University Press.Google Scholar
Hirsch, M. W., Smale, S. & Devaney, R. L. 2004 Differential Equations, Dynamical Systems, and an Introduction to Chaos. Elsevier.Google Scholar
Infeld, E. & Rolands, G. 1990 Nonlinear Waves, Soliton and Chaos. Cambridge University Press.Google Scholar
Kourakis, I., Moslem, W. M. & Abdelsalam, U. M. 2009 Nonlinear dynamics of rotating multi-component pair plasmas and e–p–i plasmas. Plasma Fusion Res. 4, 18–25.Google Scholar
Lalescu, C. C., Meneveau, C. & Eyink, G. L. 2013 Synchronization of chaos in fully developed turbulence. Nonlinear Dyn. 110, 084102.Google Scholar
Laptyeva, T. V., Bodyfelt, J. D., Krimer, D. O. & Flach, S. 2010 The crossover from strong to weak chaos for nonlinear waves in disordered systems. Europhys. Lett. 91, 30001.CrossRefGoogle Scholar
Mathieu, J. & Scott, J. 2000 An Introduction to Turbulence Flow. Cambridge University Press.CrossRefGoogle Scholar
Michel, C., Haelterman, M., Suret, P., Randoux, S., Kaiser, R. & Picozzi, A. 2011 Thermalization and condensation in an incoherently pumped passive optical cavity. Phys. Rev. A 84, 033848.Google Scholar
Mónica, A. G. & Jorge, A. G. 2012 Formation of a two-kink soliton pair in perturbed sine-Gordon models due to kink-internal-mode instabilities. Phys. Rev. E 86, 066602.Google Scholar
Moslem, W. M., Ali, S. & Shukla, P. K. 2007 Solitary, explosive, and periodic solutions of the quantum Zakharov–Kuznetsov equation and its transverse instability. Phys. Plasmas 14, 1064–1070.Google Scholar
Mulansky, M., Ahnert, K., Pikovsky, A. & Shepelyansky, D. L. 2011 Strong and weak chaos in weakly nonintegrable many-body Hamiltonian systems. J. Stat. Phys. 145, 1256–1274.Google Scholar
Mushtaq, A. & Khan, S. A. 2008 Dust ion-acoustic waves in magnetized quantum dusty plasmas with polarity effect. Phys. Plasmas 15, 013701.Google Scholar
Myatt, J., Delettrez, J. A. & Maximov, A. V. 2009 Optimizing electron–positron pair production on kilojoule-class high-intensity lasers for the purpose of pair-plasma creation. Phys. Rev. E 79, 1019–1027.Google Scholar
Pakzad, H. R., Javidan, K. & Tribeche, M. 2014 Time evolution of nonplanar electron acoustic shock waves in a plasma with superthermal electrons. Astrophys. Space Sci. 352, 185–191.Google Scholar
Pal, B., Poria, S. & Sahu, B. 2015 Instability saturation by the oscillating two-stream instability in a weakly relativistic plasma. Phys. Plasmas 22, 036407.Google Scholar
Peletan, L., Baguet, S. & Torkhani, M. 2014 Quasi-periodic harmonic balance method for rubbing self-induced vibrations in rotor-stator dynamics. Nonlinear Dyn. 78, 2501–2515.Google Scholar
Paul, R. K. 2015 Investigation on the feasibility of fusion in a compressed beam of ions subject to an electrostatic field. J. Plasma Phys. 81, 132–140.Google Scholar
Rasheed, A., Tsintsadze, N. L. & Murtaza, G. 2012 Nonlinear structure of ion-acoustic solitary waves in a relativistic degenerate electron–positron–ion plasma. J. Plasma Phys. 78, 133–141.Google Scholar
Sabry, R., Moslem, W. M. & Shukla, P. K. 2011 On the generation of envelope solitons in the presence of excess superthermal electrons and positrons. Astrophys. Space Sci. 333, 203–208.CrossRefGoogle Scholar
Safeer, S., Mahmood, S. & Haque, Q. 2014 Ion acoustic solitons in dense magnetized plasmas with nonrelativistic and ultrarelativistic degenerate electrons and positrons. Astrophys. J. 793, 36–47.Google Scholar
Sahu, B. & Tribeche, M. 2012 Nonextensive dust acoustic solitary and shock waves in nonplanar geometry. Astrophys. Space Sci. 338, 259–264.Google Scholar
Salahuddin, M., Saleem, H. & Saddiq, M. 2002 Ion-acoustic envelope solitons in electron–positron–ion plasmas. Phys. Rev. E 66, 1162–1167.Google Scholar
Seough, J., Yoon, P. H. & Kim, K. H. 2013 Solar-wind proton anisotropy versus beta relation. Phys. Rev. Lett. 110, 582–586.CrossRefGoogle ScholarPubMed
Shally, L., Murugan, S. M. R. & Rama, G. 2014 Soliton propagation in negative-index materials with self-steepening effect. Eur. Phys. J. D 68, 1621–1638.Google Scholar
Shilov, M., Cates, C. & James, R. 2004 Dynamical plasma response of resistive wall modes to changing external magnetic perturbations. Phys. Plasmas 11, 2573–2579.Google Scholar
Shukla, P. K. & Mamun, A. A. 2003 Solitons, shocks and vortices in dusty plasmas. New J. Phys. 5, 17–23.CrossRefGoogle Scholar
Stoica, P. & Moses, R. L. 1997 Introduction to Spectral Analysis. Prentice-Hall.Google Scholar
Tian, B. & Gao, Y. T. 2005 Cylindrical nebulons, symbolic computation and Bäklund transformation for the cosmic dust acoustic waves. Phys. Plasmas 12, 070703.Google Scholar
Williams, G. P. 1997 Chaos Theory Tamed. Joseph Henry.Google Scholar
Wu, G. C. & Baleanu, D. 2014 Discrete fractional logistic map and its chaos. Nonlinear Dyn. 75, 283–287.Google Scholar
Yair, Z. 2008 From single- to multiple-soliton solutions of the perturbed KdV equation. Physica D 237, 2987–3007.Google Scholar
Zhang, R. X. & Yang, S. P. 2011 Adaptive synchronization of fractional-order chaotic systems via a single driving variable. Nonlinear Dyn. 66, 831–837.Google Scholar
Zhang, X., Shen, X., Liu, J., Ouyang, X., Qian, J. & Zhao, S. 2009 Analysis of ionospheric plasma perturbations before Wenchuan earthquake. Nat. Hazards Earth Syst. Sci. 9, 1259–1266.Google Scholar
Zobaer, M. S., Nahar, L. & Mukta, K. N. 2013 KdV and Burgers equations on DA waves with strongly coupled dusty plasma. Astrophys. Space Sci. 346, 351–357.Google Scholar