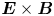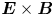2. Electrostatic potential in curved magnetic fields

Consider a plasma system consisting of ions and electrons. Let $n_e$ denote the electron density. We assume that $n_e$ follows a Boltzmann distribution with constant temperature $T_e>0$:

(2.1)\begin{equation} n_e=A_e\exp\left\{-\frac{q\phi}{k_BT_e}\right\}. \end{equation}

Here, $A_e\left ({\boldsymbol {x}}\right )$ is a positive spatial function, $\phi$ denotes the electric potential, $q=-e$ is the electron charge and $k_B$ is the Boltzmann constant. It is convenient to introduce the constant

(2.2)\begin{equation} \lambda=\frac{e}{k_BT_e}. \end{equation}

Let $\boldsymbol {B}=\boldsymbol {B}\left ({\boldsymbol {x}}\right )$ denote a static magnetic field. Recall that $\boldsymbol {B}$ must be solenoidal, ${\boldsymbol {\nabla }}\boldsymbol {\cdot }\boldsymbol {B}=0$. In the following, we demand that $\boldsymbol {B}\neq 0$ throughout the domain of interest $V$. Let $n$ denote the ion density. Assuming quasi-neutrality, $n_e=Zn$ with $Z$ the number of protons in the ions. Using (2.1), the ion continuity equation reads

(2.3)\begin{equation} \lambda\phi_t={-} {\boldsymbol{\nabla}}\boldsymbol{\cdot}\boldsymbol{v}-\lambda\boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{\nabla}\phi-\boldsymbol{\nabla}\log{A_e}\boldsymbol{\cdot}\boldsymbol{v}. \end{equation}

Here, $\boldsymbol {v}$ denotes the ion fluid velocity. On the other hand, denoting with $m$ the ion mass, the ion fluid equation of motion can be written as

(2.4)\begin{equation} m n\frac{{\rm d}\boldsymbol{v}}{{\rm d}t}=Ze n\left({\boldsymbol{v}\times\boldsymbol{B}+\boldsymbol{E}}\right)-\boldsymbol{\nabla} P,\end{equation}

where $P$ represents pressure and $\boldsymbol {E}=-\boldsymbol {\nabla }\phi$ the electric field. It is convenient to decompose the ion fluid velocity as

(2.5)\begin{equation} \boldsymbol{v}=\boldsymbol{v}_{{\parallel}}+\boldsymbol{v}_{{\perp}}, \end{equation}

where $\boldsymbol {v}_{\parallel }$ denotes the velocity component along the magnetic field and $\boldsymbol {v}_{\perp }$ the perpendicular one. In the two-dimensional drift turbulence setting, the parallel velocity component is neglected because the time scale of fluctuations $t_d$ is faster than the time scale $t_b$ of ion dynamics along the magnetic field, $t_d\ll t_b$. In the following, we will therefore put

(2.6)\begin{equation} \boldsymbol{v}_{{\parallel}}=\boldsymbol{0}, \end{equation}

and discard the dynamics along $\boldsymbol {B}$. In this context, it is of interest to study the long-term evolution of coherent structures. It is worth noticing that in the opposite regime $t_d\gg t_b$ the parallel motion $\boldsymbol {v}_{\parallel }$ gets averaged out as well due to the fast bounce oscillation, although the polarization drift becomes neoclassically enhanced due to a large orbit size, leading to a neoclassically modified turbulence model with a dominant Hasegawa–Mima-type polarization nonlinearity (Hahm & Tang Reference Hahm and Tang1996). To proceed, we introduce a reference time scale $t_c$ and a reference length scale $L_{\perp }$ across $\boldsymbol {B}$, and take $k_BT_e$ as reference value for the energy. In the standard drift turbulence ordering $t_c=2{\rm \pi} /\varOmega _c$, with $\varOmega _c=ZeB/m$ the ion cyclotron frequency, while $L_{\perp }$ corresponds to the sound radius $\rho _s=c_s\varOmega _{c}^{-1}\sim k_{\perp }^{-1}$, where $c_s=\left ({Zk_BT_e/m}\right )^{1/2}$ is the sound speed and $k_{\perp }$ a characteristic perpendicular wavenumber for the turbulence. In this study we further consider a regime of plasma where the electric potential energy is small compared with the electron kinetic energy, and the ratio between the component of the electric field perpendicular to the magnetic field and the magnetic field itself is small:

(2.7a,b)\begin{equation} \left\lvert{\frac{e\phi}{k_BT_e}}\right\rvert\sim\epsilon,\quad \frac{t_c E_{{\perp}}}{L_{{\perp}} B}\sim\epsilon, \end{equation}

where $\epsilon \ll 1$ is a small ordering parameter, $E_{\perp }=\left \lvert {\boldsymbol {E}_{\perp }}\right \rvert$, with $\boldsymbol {E}_{\perp }$ the component of the electric field $\boldsymbol {E}$ perpendicular to $\boldsymbol {B}$, and $B=\left \lvert {\boldsymbol {B}}\right \rvert$. The remaining perpendicular component $\boldsymbol {v}_{\perp }$ can be expanded into a first-order term $\boldsymbol {v}_{1}$, which will correspond to first-order $\boldsymbol {E}\times \boldsymbol {B}$ drift dynamics, a second-order term $\boldsymbol {v}_{2}$, which will be identified with second-order $\boldsymbol {E}\times \boldsymbol {B}$ drift dynamics plus the polarization drift encountered in guiding centre theory, and higher-order corrections. At second order in $\epsilon$ we therefore have

(2.8)\begin{equation} \boldsymbol{v}=\boldsymbol{v}_{{\perp}}=\epsilon\boldsymbol{v}_{1}+\epsilon^2\boldsymbol{v}_{2}. \end{equation}

To proceed, a further working assumption is needed on the rate of change of $\boldsymbol {v}$, which may only evolve on time scales long relative to a gyroperiod:

(2.9)\begin{equation} \frac{t_c}{\left\lvert{\boldsymbol{v}}\right\rvert}\frac{\partial\boldsymbol{v}}{\partial t}\ll 1. \end{equation}

Recalling the decomposition (2.8), (2.9) leads to

(2.10a,b)\begin{equation} \frac{t_c^2}{L_{{\perp}}}\left\lvert{\frac{\partial\boldsymbol{v}_1}{\partial t}}\right\rvert\sim \epsilon,\quad \frac{t_c^2}{L_{{\perp}}}\left\lvert{\frac{\partial\boldsymbol{v}_2}{\partial t}}\right\rvert\sim\epsilon. \end{equation}

Furthermore, we enforce the cold ion hypothesis $T=0$, with $T$ the ion temperature, implying that ions are not subject to thermal fluctuations, and therefore

(2.11)\begin{equation} P=0. \end{equation}

To obtain expressions for $\boldsymbol {v}_{1}$ and $\boldsymbol {v}_{2}$, consider again the equation of motion (2.4), which at second order in $\epsilon$ now reads as

(2.12)\begin{equation} \epsilon Ze\left({\boldsymbol{B}\times\boldsymbol{v}_{1}-\boldsymbol{E}_1}\right)=\epsilon^2\left[{-}m\frac{{\rm d}\boldsymbol{v}_1}{{\rm d}t}+Ze \left({\boldsymbol{v}_{2}\times\boldsymbol{B}+\boldsymbol{E}_2}\right)\right]. \end{equation}

Here, we used (2.10a,b) to extract the order of $\partial \boldsymbol {v}_{1}/\partial t$ according to $\partial \boldsymbol {v}_{1}/\partial t\rightarrow \epsilon \partial \boldsymbol {v}_1/\partial t$. In addition, the electric potential $\phi$ and electric field $\boldsymbol {E}$ have been decomposed into first-order and second-order components according to

(2.13a,b)\begin{equation} \phi=\epsilon\phi_1+\epsilon^2\phi_2,\quad \boldsymbol{E}=\epsilon\boldsymbol{E}_1+\epsilon^2\boldsymbol{E}_2={-}\epsilon\boldsymbol{\nabla}\phi_1-\epsilon^2\boldsymbol{\nabla}\phi_2. \end{equation}

Hence, the cross product of (2.12) with $\boldsymbol {B}/B^2$ can be cast in the form

(2.14)\begin{equation} \epsilon\left({\frac{\boldsymbol{E}_1\times\boldsymbol{B}}{B^2}-\boldsymbol{v}_{1}}\right)=\epsilon^2\left[-\sigma\frac{\boldsymbol{B}\times\dfrac{{\rm d}\boldsymbol{v}_1}{{\rm d}t}}{B^2}+\boldsymbol{v}_{2}+\frac{\boldsymbol{B}\times\boldsymbol{E}_2}{B^2}\right], \end{equation}

where we introduced the physical constant

(2.15)\begin{equation} \sigma=\frac{m}{Ze}. \end{equation}

Notice that all terms on the left-hand side of (2.14) are first order in $\epsilon$, while those on the right-hand side are second order. The first-order $\boldsymbol {E}\times \boldsymbol {B}$ flow $\boldsymbol {v}_{\boldsymbol {E}_1}$ can be obtained from the left-hand side:

(2.16)\begin{equation} \boldsymbol{v}_{1}=\boldsymbol{v}_{\boldsymbol{E}_1}=\frac{\boldsymbol{E}_1\times\boldsymbol{B}}{B^2}. \end{equation}

Similarly, the second-order fluid drift is given by

(2.17)\begin{equation} \boldsymbol{v}_{2}=\boldsymbol{v}_{\rm pol}+\boldsymbol{v}_{\boldsymbol{E}_2}=\sigma\frac{\boldsymbol{B}\times\dfrac{{\rm d}\boldsymbol{v}_1}{{\rm d}t}}{B^2}+\frac{\boldsymbol{E}_2\times\boldsymbol{B}}{B^2}. \end{equation}

Evidently, the second term on the right-hand side is a second-order $\boldsymbol {E}\times \boldsymbol {B}$ drift $\boldsymbol {v}_{\boldsymbol {E}_2}$, while the first term is nothing but a polarization drift $\boldsymbol {v}_{\rm pol}$ (see Hazeltine & Waelbroeck Reference Hazeltine and Waelbroeck1998). Indeed, in a straight magnetic field $\boldsymbol {B}=B_0\boldsymbol {\nabla } z$ with $B_0\in \mathbb {R}$ one has

(2.18)\begin{equation} \boldsymbol{v}_{\rm pol}=\sigma\frac{\boldsymbol{B}\times\dfrac{{\rm d}\boldsymbol{v}_1}{{\rm d}t}}{B^2}=\frac{\sigma}{B_0^2}\frac{{\rm d}\boldsymbol{E}_{1\perp}}{{\rm d}t}, \end{equation}

with $\boldsymbol {E}_{1\perp }$ the component of $\boldsymbol {E}_1$ perpendicular to $\boldsymbol {B}$. Combining equations (2.16) and (2.17), the total ion velocity has the expression

(2.19)\begin{align} \boldsymbol{v}& =\epsilon\boldsymbol{v}_{\boldsymbol{E}_1}-\epsilon^2\sigma\frac{\boldsymbol{B}\times\left[\boldsymbol{v}_{\boldsymbol{E}_1}\times\left({\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}_1}}\right)\right]}{B^2}-\epsilon^2\sigma\frac{\partial}{\partial t}\frac{\boldsymbol{\nabla}_{{\perp}}\phi_1}{B^2}+\epsilon^2\sigma\frac{\boldsymbol{B}\times\boldsymbol{\nabla}\left({\boldsymbol{v}_{\boldsymbol{E}_1}^2+\phi_2}\right)}{2B^2}\nonumber\\ & =\epsilon\left({1-\epsilon\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}_1}}{B^2}}\right)\boldsymbol{v}_{\boldsymbol{E}_1}-\epsilon^2\sigma\frac{\partial}{\partial t}\frac{\boldsymbol{\nabla}_{{\perp}}\phi_1}{B^2}+\epsilon^2\sigma\frac{\boldsymbol{B}\times\boldsymbol{\nabla}\left({\boldsymbol{v}_{\boldsymbol{E}_1}^2+\phi_2}\right)}{2B^2}, \end{align}

where we introduced the orthogonal gradient operator

(2.20)\begin{equation} \boldsymbol{\nabla}_{{\perp}}f=\frac{\boldsymbol{B}\times\left({\boldsymbol{\nabla} f\times\boldsymbol{B}}\right)}{B^2}, \end{equation}

with $f$ some function. Then, we have

(2.21)\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{v}= \boldsymbol{\nabla}\boldsymbol{\cdot}\left[ \epsilon\left({1-\epsilon\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}_1}}{B^2}}\right)\boldsymbol{v}_{\boldsymbol{E}_1} \right] -\epsilon^2\sigma\frac{\partial}{\partial t}\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{\boldsymbol{\nabla}_{{\perp}}\phi_1}{B^2}}\right)\nonumber\\ + \frac{1}{2}\epsilon^2\sigma\boldsymbol{\nabla}\left({\boldsymbol{v}_{\boldsymbol{E}_1}^2+\phi_2}\right)\boldsymbol{\cdot}\boldsymbol{\nabla}\times\left({\frac{\boldsymbol{B}}{B^2}}\right). \end{gather}

Defining the total $\boldsymbol {E}\times \boldsymbol {B}$ drift velocity as

(2.22)\begin{equation} \boldsymbol{v}_{\boldsymbol{E}}=\epsilon\boldsymbol{v}_{\boldsymbol{E}_1}+\epsilon^2\boldsymbol{v}_{\boldsymbol{E}_2}=\frac{\boldsymbol{E}\times\boldsymbol{B}}{B^2}, \end{equation}

at second order equation (2.19) can be expressed solely in terms of $\phi$ as

(2.23)\begin{align} \boldsymbol{v}& =\boldsymbol{v}_{\boldsymbol{E}}-\sigma\frac{\boldsymbol{B}\times\left[\boldsymbol{v}_{\boldsymbol{E}}\times\left({\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}\right)\right]}{B^2}-\sigma\frac{\partial}{\partial t}\frac{\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}+\sigma\frac{\boldsymbol{B}\times\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2}{2B^2}\nonumber\\ & =\left({1-\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}}\right)\boldsymbol{v}_{\boldsymbol{E}}-\sigma\frac{\partial}{\partial t}\frac{\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}+\sigma\frac{\boldsymbol{B}\times\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2}{2B^2}. \end{align}

We remark that this same result can also be obtained by a simple iteration method where, regarding the left-hand side of (2.4) as a smaller term than the right-hand side, we have the lowest-order solution as $\boldsymbol {v}=\boldsymbol {v}_{\boldsymbol {E}}$ and the next-order solution as given by (2.23). Similarly, in terms of $\phi$, (2.21) can be written as

(2.24)\begin{align} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{v}& = \boldsymbol{\nabla}\boldsymbol{\cdot}\left[ \left({1-\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}}\right)\boldsymbol{v}_{\boldsymbol{E}} \right] -\sigma\frac{\partial}{\partial t}\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}}\right)\nonumber\\ & \quad + \frac{1}{2}\sigma\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2\boldsymbol{\cdot}\boldsymbol{\nabla}\times\left({\frac{\boldsymbol{B}}{B^2}}\right). \end{align}

On the other hand, the term

(2.25)\begin{equation} \lambda\boldsymbol{v}\boldsymbol{\cdot}{\boldsymbol{\nabla}}\phi =\epsilon^3\lambda\left({\boldsymbol{v}_1\boldsymbol{\cdot}\boldsymbol{\nabla}\phi_2+\boldsymbol{v}_2\boldsymbol{\cdot}\boldsymbol{\nabla}\phi_1+\epsilon\boldsymbol{v}_2\boldsymbol{\cdot}\boldsymbol{\nabla}\phi_2}\right) \end{equation}

appearing on the right-hand side of (2.3) is a third-order contribution that can be neglected. Using (2.24) and (2.25) to evaluate (2.3), at second order we thus obtain

(2.26)\begin{align} \frac{\partial}{\partial t}\left[\lambda A_e\phi -\sigma\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{A_e\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}}\right)\right]= \boldsymbol{\nabla}\boldsymbol{\cdot}\left[ A_e\left({\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}-1}\right)\boldsymbol{v}_{\boldsymbol{E}} -\sigma A_e\frac{\boldsymbol{B}\times\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2}{2B^2} \right]. \end{align}

To check the consistency of the ordering assumptions leading to (2.26) we must verify that the ion fluid conservation laws are satisfied by the derived equation. First consider the total mass

(2.27)\begin{equation} M_V=m\int_{V}n\,{\rm d}V. \end{equation}

In this notation $V\subset \mathbb {R}^3$ is a bounded domain occupied by the plasma and ${\rm d}V$ the volume element in $\mathbb {R}^3$. The constancy of $M$ follows immediately by noting that at leading order in $\phi$

(2.28)\begin{equation} M_V=m\int_{V}A_e\left({1+\lambda\phi}\right)\,{\rm d}V. \end{equation}

Then, using (2.26) and (2.23) we have

(2.29)\begin{equation} \frac{{\rm d}M_V}{{\rm d}t}={-}m\int_{\partial V}A_e\boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{n}\,{\rm d}S, \end{equation}

where $\boldsymbol {n}$ is the unit outward normal to the boundary $\partial V$, ${\rm d}S$ is the surface element on $\partial V$ and $\boldsymbol {v}$ is given by (2.23). This boundary integral vanishes if the system is periodic or the fluid velocity $\boldsymbol {v}$ is tangential to the bounding surface, $\boldsymbol {v}\boldsymbol {\cdot }\boldsymbol {n}=0$ on $\partial V$, or $A_e=0$ on $\partial V$. Next, consider the fluid energy

(2.30)\begin{equation} E_V=\int_{V}n\left({\frac{1}{2}m\boldsymbol{v}^2+Ze\phi}\right)\,{\rm d}V. \end{equation}

To study conservation of energy it is convenient to subtract from $E_V$ the total mass $M_V$ and define a new quantity:

(2.31)\begin{equation} H_V=\frac{E_V}{Ze}-\frac{M_V}{m\lambda}=\int_V n\left({\frac{1}{2}\sigma\lambda\boldsymbol{v}^2+\lambda\phi^2-\frac{1}{\lambda}}\right)\,{\rm d}V. \end{equation}

At leading order in $\phi$ we therefore obtain

(2.32)\begin{equation} H_{V}=\frac{1}{2}\int_{V}A_e\left({\sigma\boldsymbol{v}_{\boldsymbol{E}}^2+\lambda\phi^2-\frac{2}{\lambda}}\right)\,{\rm d}V. \end{equation}

Since $A_e\left ({\boldsymbol {x}}\right )$ is independent of time, the quantity $H_V$ can be further simplified to

(2.33)\begin{equation} H_{V}=\frac{1}{2}\int_{V}A_e\left({\lambda\phi^2+\sigma\frac{\left\lvert{\boldsymbol{\nabla}_{{\perp}}\phi}\right\rvert^2}{B^2}}\right)\,{\rm d}V.\end{equation}

Using (2.26), the rate of change in $H_V$ is

(2.34)\begin{align} \frac{{\rm d}H_V}{{\rm d}t}& =\int_{V}A_e\left({\lambda\phi\phi_t+\frac{\sigma}{B^2}\boldsymbol{\nabla}\phi\boldsymbol{\cdot}\boldsymbol{\nabla}_{{\perp}}\phi_t}\right)\,{\rm d}V\nonumber\\ & =\int_{V}{\phi\left[\lambda A_e\phi_t-\sigma\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{A_e\boldsymbol{\nabla}_{{\perp}}\phi_t}{B^2}}\right)\right]}\,{\rm d}V+\sigma\int_{\partial V}A_e\phi\frac{\boldsymbol{\nabla}_{{\perp}}\phi_t}{B^2}\boldsymbol{\cdot}\boldsymbol{n}\,{\rm d}S\nonumber\\ & =\int_{V}\phi\boldsymbol{\nabla}\boldsymbol{\cdot}\left[A_e\left({\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}-1}\right)\boldsymbol{v}_{\boldsymbol{E}}-\sigma A_e\frac{\boldsymbol{B}\times\boldsymbol{\nabla}\boldsymbol{v}^2_{\boldsymbol{E}}}{2B^2}\right]\,{\rm d}V\nonumber\\ & \quad +\sigma\int_{\partial V}A_e\phi \frac{\boldsymbol{\nabla}_{{\perp}}\phi_t}{B^2}\boldsymbol{\cdot}\boldsymbol{n}\,{\rm d}S\nonumber\\ & =\int_{\partial V}A_e\phi\left[\left({\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}-1}\right)\boldsymbol{v}_{\boldsymbol{E}}-\sigma\frac{\boldsymbol{B}\times\boldsymbol{\nabla\boldsymbol{v}_{\boldsymbol{E}}^2}}{2B^2}+\sigma\frac{\boldsymbol{\nabla}_{{\perp}}\phi_t}{B^2}\right]\boldsymbol{\cdot}\boldsymbol{n}\,{\rm d}S\nonumber\\ & \quad-\frac{1}{2}\sigma\int_{V}A_e\boldsymbol{v}_{\boldsymbol{E}}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2\,{\rm d}V\nonumber\\ & ={-}\int_{\partial V}A_e\phi\,\boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{n}\,{\rm d}S-\frac{1}{2}\sigma\int_{V}A_e\boldsymbol{v}_{\boldsymbol{E}}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2\,{\rm d}V. \end{align}

Here, $\boldsymbol {v}$ is given by (2.23) and the notation $\phi _t=\partial \phi /\partial t$ has been used. Notice that boundary integrals vanish if the system is periodic or $\boldsymbol {v}\boldsymbol {\cdot }\boldsymbol {n}=0$ on $\partial V$ or $A_e\phi =0$ on $\partial V$.

However, the last term on the right-hand side cannot be written as a boundary integral. Hence, an additional ordering condition is needed to ensure that energy is preserved. This term originates from the quantity

(2.35)\begin{equation} \sigma\boldsymbol{\nabla}\boldsymbol{\cdot}\left({A_e\frac{\boldsymbol{B}\times\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2}{2B^2}}\right)=\frac{1}{2}\sigma\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2\boldsymbol{\cdot}\boldsymbol{\nabla}\times\left({\frac{A_e\boldsymbol{B}}{B^2}}\right) \end{equation}

appearing on the right-hand side of (2.26). We therefore demand that

(2.36)\begin{equation} \frac{t_c\sigma}{2A_e}\left\lvert{\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2\boldsymbol{\cdot}\boldsymbol{\nabla}\times\left({\frac{A_e\boldsymbol{B}}{B^2}}\right)}\right\rvert\sim\epsilon^3. \end{equation}

Observe that the scaling above reflects the degree of accuracy of the ordering assumption $t^2_c L_{\perp }^{-1}\partial \boldsymbol {v}_{2}/\partial t\sim \epsilon$ adopted in (2.10a,b) which led to the omission of this term from fluid momentum balance. Recalling that $\boldsymbol {v}_{\boldsymbol {E}}^2$ is second order in $\epsilon$, if the density gradient is small $L_{\perp }\left \lvert {\boldsymbol {\nabla }_{\perp }A_e}\right \rvert /A_e\sim \epsilon$ the condition (2.36) is automatically satisfied for those magnetic fields such that $B_0L_{\perp }\left \lvert {\boldsymbol {\nabla }\times \left ({B^{-2}\boldsymbol {B}}\right )}\right \rvert \sim \epsilon$, with $B_0\in \mathbb {R}$ a reference magnetic field, or equivalently

(2.37)\begin{equation} \boldsymbol{B}=B^2\left({\boldsymbol{\nabla}\zeta+\epsilon\boldsymbol{\xi}}\right) \end{equation}

for some potential $\zeta$ and vector field $\boldsymbol {\xi }$. This condition implies that the quantity $\boldsymbol {B}/B^2$ does not depart largely from a potential field, physically implying that the divergence of the $\boldsymbol {E}\times \boldsymbol {B}$ velocity scales as $t_c\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v}_{\boldsymbol {E}}=t_c\epsilon \boldsymbol {\nabla }\times \boldsymbol {\xi }\boldsymbol {\cdot }\boldsymbol {\nabla }\phi \sim \epsilon ^2$. This is the case of the standard Hasegawa–Mima equation, where $L_{\perp }\left \lvert {\boldsymbol {\nabla }_{\perp } A_e}\right \rvert /A_e\sim \epsilon$ and (2.36) is satisfied with $\zeta =B_0^{-1}z$, $B_0\in \mathbb {R}$ and $\boldsymbol {\xi }=\boldsymbol {0}$ so that $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v}_{\boldsymbol {E}}=0$. An alternative way to fulfil (2.36) is to assume that

(2.38)\begin{equation} L_{{\perp}}\left\lvert{\boldsymbol{\nabla}\boldsymbol{v}_{\boldsymbol{E}}^2}\right\rvert\sim\epsilon\boldsymbol{v}_{\boldsymbol{E}}^2,\end{equation}

implying a mild change in $\boldsymbol {E}\times \boldsymbol {B}$ drift velocity across $\boldsymbol {B}$ as in the case for large-scale coherent structures studied in § 3.

Once the prescription (2.36) is enforced, the last term in (2.26) can be neglected since it scales as $\epsilon ^3$, and we obtain a consistent equation for the potential $\phi$,

(2.39)\begin{equation} \frac{\partial}{\partial t}\left[\lambda A_e\phi -\sigma\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{A_e\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}}\right)\right]= \boldsymbol{\nabla}\boldsymbol{\cdot}\left[ A_e\left({\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}-1}\right)\boldsymbol{v}_{\boldsymbol{E}} \right], \end{equation}

which preserves the total mass (2.28) and the energy (2.33) exactly under suitable boundary conditions. In particular, one obtains

(2.40a,b)\begin{equation} \frac{{\rm d}M_{V}}{{\rm d}t}={-}m\int_{\partial V}A_e\boldsymbol{v}'\boldsymbol{\cdot}\boldsymbol{n}\,{\rm d}S,\quad \frac{{\rm d}H_{V}}{{\rm d}t}={-}\int_{\partial V}A_e\phi\,\boldsymbol{v}'\boldsymbol{\cdot}\boldsymbol{n}\,{\rm d}S, \end{equation}

with the effective ion fluid velocity

(2.41)\begin{equation} \boldsymbol{v}'=\left({1-\sigma\frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}}\right)\boldsymbol{v}_{\boldsymbol{E}}-\sigma\frac{\partial}{\partial t}\frac{\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}. \end{equation}

The conditions on magnetic field topology for the existence of an additional conserved quantity (generalized enstrophy) are discussed in § 4.

We suggest that (2.39) is appropriate to describe electrostatic turbulence in magnetic fields with arbitrary topology. In particular, considering the ordering condition (2.36), the equation is best suited for magnetic fields of the type (2.37) so that $t_c\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v}_{\boldsymbol {E}}\sim \epsilon ^2$, or for configurations (2.38) such that the spatial change in $\boldsymbol {E}\times \boldsymbol {B}$ drift velocity scales as $t^2_cL_{\perp }^{-1}\boldsymbol {\nabla }\boldsymbol {v}_{\boldsymbol {E}}^2\sim \epsilon ^3$.

It should be noted that (2.39) can be derived from the standard drift turbulence ordering $e\phi /k_BT_e\sim \varOmega _c^{-1}\partial /\partial t\sim \epsilon$, $k_\perp L_{\perp }'\sim k_{\perp }L_{n_e}\sim k_{\perp }/k_{\parallel }\sim \epsilon ^{-1}$ and $k_{\perp }\rho _s\sim 1$, where $L_{\perp }'$ is a large perpendicular scale associated with the spatial change in $\boldsymbol {B}$, $L_{n_e}\sim A_e/\left \lvert {\boldsymbol {\nabla }_{\perp } A_e}\right \rvert$ the characteristic spatial scale associated with the density $n_e$, $k_{\parallel }$ a characteristic wavenumber along the magnetic field, $\rho _s=c_sm/ZeB$ the sound radius and $c_s=(Zk_BT_e/m)^{1/2}$ the sound speed. With such ordering the last term in (2.26) can be discarded from the outset, being a third-order contribution. However, this comes at the price of additional constraints on the spatial change allowed for $\boldsymbol {B}$, since all its spatial derivatives $L_{\perp }\nabla \sim 1/k_{\perp }L_{\perp }'\sim \epsilon$ must be small.

Regarding the physical interpretation of the terms appearing in the equation, it is worth observing that the quantity $\boldsymbol {\nabla }\boldsymbol {\cdot }\left ({B^{-2}\boldsymbol {\nabla }_{\perp }\phi }\right )$ arises from the component of the vorticity $\boldsymbol {\nabla }\times \boldsymbol {v}_{\boldsymbol {E}}$ along $\boldsymbol {B}$. Indeed,

(2.42)\begin{equation} \frac{\boldsymbol{B}}{B^2}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}=\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}}\right)+\left[\boldsymbol{\nabla}\times\left({\frac{\boldsymbol{B}}{B^2}}\right)\right]\times\frac{\boldsymbol{B}}{B^2}\boldsymbol{\cdot}\boldsymbol{\nabla}_{{\perp}}\phi. \end{equation}

In addition, a term $\boldsymbol {\nabla }\boldsymbol {\cdot }\left ({nB^{-2}\boldsymbol {\nabla }_{\perp }\phi }\right )$ is often encountered in modern gyrokinetic and gyrofluid theories as the ion polarization charge density in Poisson's equation for the electric potential (Strinzi & Scott Reference Strinzi and Scott2004; Hahm, Wang & Madsen Reference Hahm, Wang and Madsen2009). The factor $1-\sigma B^{-2} \boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\times \boldsymbol {v}_{\boldsymbol {E}}$ on the right-hand side of (2.39) is similarly predicted by gyrokinetic theory as a correction caused by the polarization charge-like term to the effective magnetic field strength:

(2.43)\begin{equation} B_{{\parallel}}^{{\ast}}\simeq B\left({1+\sigma \frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}}\right), \end{equation}

which corresponds to the Jacobian determinant of the guiding centre phase space when parallel dynamics is ignored. This correction causes a net drift velocity (see equation (4) of Hahm (Reference Hahm1996) or the discussion in Littlejohn (Reference Littlejohn1981)):

(2.44)\begin{equation} \tilde{\boldsymbol{v}}_{\boldsymbol{E}}=\frac{\boldsymbol{B}\times\boldsymbol{\nabla}\phi}{BB_{{\parallel}}^{{\ast} }}\simeq \left({1-\sigma \frac{\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}}{B^2}}\right)\boldsymbol{v}_{\boldsymbol{E}}. \end{equation}

3. Limit to the Hasegawa–Mima equation and curvature effects

In this section we show that (2.39) reduces to the Hasegawa–Mima equation (Hasegawa & Mima Reference Hasegawa and Mima1977a) when the magnetic field is straight, $\boldsymbol {B}=B_0\boldsymbol {\nabla } z$ with $B_0\in \mathbb {R}$. In the remainder of this paper, we restrict our attention to the constant density case $A_e\in \mathbb {R}$. In tokamak turbulence this condition can occur in the core of H-mode plasmas (Bernert et al. Reference Bernert, Eich, Kallenbach, Carralero, Huber, Lang, Potzel, Reimold, Schweinzer and Viezzer2015) where density is often well approximated by a flat profile.

Before proceeding further, it should be noted that in many cases of practical interest the magnetic field varies on spatial scales $L_{\perp }$ that are larger than the sound radius $\rho _s$, i.e. $\rho _s/L_{\perp }\sim \epsilon$. If both magnetic field and electric potential vary on the macroscopic spatial scale $L_{\perp }$, the terms $\boldsymbol {\nabla }\boldsymbol {\cdot }\left ({A_e\boldsymbol {v}_{\boldsymbol {E}}}\right )$ and $\boldsymbol {\nabla }\boldsymbol {\cdot }\left ({({\sigma }/{2})({A_e\boldsymbol {B}}/{B^2})\times \boldsymbol {\nabla } \boldsymbol {v}_{\boldsymbol {E}}^2}\right )$ on the right-hand side of (2.26) become comparable third-order terms because

(3.1)\begin{align} \dfrac{\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\dfrac{\sigma}{2}\dfrac{A_e\boldsymbol{B}}{B^2}\times\boldsymbol{\nabla} \boldsymbol{v}_{\boldsymbol{E}}^2}\right)}{\boldsymbol{\nabla}\boldsymbol{\cdot}\left({A_e\boldsymbol{v}_{\boldsymbol{E}}}\right)}= \dfrac{\dfrac{\sigma}{2}{\boldsymbol{\nabla} \boldsymbol{v}_{\boldsymbol{E}}^2}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\left({\dfrac{A_e\boldsymbol{B}}{B^2}}\right)}{\boldsymbol{\nabla} \boldsymbol{\cdot}\left({A_e\boldsymbol{v}_{\boldsymbol{E}}}\right)}\sim \epsilon^3\dfrac{\varOmega_c}{v_E/L_{{\perp}}} \sim \epsilon^3\dfrac{\varOmega_ceBL_{{\perp}}^2}{mc^2_s/Z}\dfrac{k_BT_e}{e\phi} \sim \epsilon^2\dfrac{L_\perp^2}{\rho_s^2}. \end{align}

Hence, in this scenario the ordering breaks down. However, physical settings with $\rho _s/L_{\perp }\sim \epsilon$ can still be handled by invoking the standard Hasegawa–Mima ordering (which leads to the same (2.39) as previously explained) where the magnetic field changes on the large spatial scale $L_{\perp }$, while the electric potential is characterized by the smaller scale length $\rho _s$.

To elucidate how a curved inhomogeneous magnetic field modifies the Hasegawa–Mima equation, it is convenient to study (2.39) in the limit of a magnetic field of the type

(3.2)\begin{equation} \boldsymbol{B}=B_0\boldsymbol{\nabla} z+\epsilon_{B}\boldsymbol{a}, \end{equation}

where $\epsilon _{B}\ll 1$ is an ordering parameter and $\boldsymbol {a}=\left ({a_x,a_y,a_z}\right )$ a vector field such that $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {a}=0$. For simplicity, we assume that $a_z=\boldsymbol {a}\boldsymbol {\cdot }\boldsymbol {\nabla } z=0$. Notice that the magnetic field (3.2) satisfies (2.37) and thus (2.36) as well. Furthermore, at the first order in $\epsilon _B$ the curvature of the magnetic field (3.2) is given by

(3.3)\begin{equation} \boldsymbol{\kappa}=\frac{\boldsymbol{B}}{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\left({\frac{\boldsymbol{B}}{B}}\right)=\frac{\epsilon_B}{B_0}\frac{\partial\boldsymbol{a}}{\partial z}.\end{equation}

It is convenient to introduce the two-dimensional gradient and Laplacian operators:

(3.4a,b)\begin{equation} \boldsymbol{\nabla}_{\left({x,y}\right)}f=\frac{\partial f}{\partial x}\boldsymbol{\nabla} x+\frac{\partial f}{\partial y}\boldsymbol{\nabla} y,\quad \Delta_{\left({x,y}\right)}f= \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}, \end{equation}

where $f=f\left ({x,y,z}\right )$ is some function. Then, at first order in $\epsilon _B$ we have

(3.5a)\begin{gather} B^2=B_0^2, \end{gather}

(3.5b)\begin{gather}\boldsymbol{\nabla}_\perp\phi=\boldsymbol{\nabla}_{\left({x,y}\right)}\phi-\frac{\epsilon_B}{B_0}\left[ \left({\boldsymbol{a}\boldsymbol{\cdot}\boldsymbol{\nabla}\phi}\right)\boldsymbol{\nabla} z+\frac{\partial\phi}{\partial z}\boldsymbol{a} \right], \end{gather}

(3.5c)\begin{gather}\boldsymbol{v}_{\boldsymbol{E}}=\frac{\boldsymbol{\nabla} z\times\boldsymbol{\nabla}\phi}{B_0}+\frac{\epsilon_B}{B_0^2}\boldsymbol{a}\times\boldsymbol{\nabla}\phi, \end{gather}

(3.5d)\begin{gather}\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{v}_{\boldsymbol{E}}=\frac{\epsilon_B}{B_0^2}\boldsymbol{\nabla}\phi\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{a}, \end{gather}

(3.5e)\begin{gather}\boldsymbol{\nabla}\times\boldsymbol{v}_{\boldsymbol{E}}=\frac{\Delta_{\left({x,y}\right)}\phi}{B_0}\boldsymbol{\nabla} z +\frac{\epsilon_B}{B_0^2}\boldsymbol{\nabla}\times\left({\boldsymbol{a}\times\boldsymbol{\nabla}\phi}\right)-\frac{1}{B_0}\boldsymbol{\nabla}_{\left({x,y}\right)}\frac{\partial \phi}{\partial z}. \end{gather}

Hence, defining the bracket

(3.6)\begin{equation} \left[f,g\right]_{\left({x,y}\right)}=\frac{\partial f}{\partial x}\frac{\partial g}{\partial y}-\frac{\partial f}{\partial y}\frac{\partial g}{\partial x}, \end{equation}

with $f,g$ some functions, (2.39) becomes

(3.7)\begin{align} & \frac{\partial}{\partial t}\left[ \lambda\phi-\frac{\sigma}{B_0^2}\Delta_{\left({x,y}\right)}\phi +\frac{\epsilon_B\sigma}{B_0^3}\frac{\partial\boldsymbol{a}}{\partial z}\boldsymbol{\cdot}\boldsymbol{\nabla}\phi+\frac{2\epsilon_B\sigma}{B_0^3}\boldsymbol{a}\boldsymbol{\cdot}\boldsymbol{\nabla}\left({\frac{\partial\phi}{\partial z}}\right) \right]\nonumber\\ & \quad=\frac{\sigma}{B_0^3}\left[ \phi,\Delta_{\left({x,y}\right)}\phi-\frac{2\epsilon_B}{B_0}\boldsymbol{a}\boldsymbol{\cdot}\boldsymbol{\nabla}\left({\frac{\partial\phi}{\partial z}}\right) \right]_{\left({x,y}\right)}\nonumber\\ & \qquad -\frac{\epsilon_B}{B_0^2}\left({1-\frac{\sigma}{B_0^2}\Delta_{\left({x,y}\right)}\phi}\right)\boldsymbol{\nabla}\phi\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{a}\nonumber\\ & \qquad+\frac{\sigma\epsilon_B}{B_0^4}\boldsymbol{\nabla}\phi\boldsymbol{\cdot}\boldsymbol{\nabla}\left({\Delta_{\left({x,y}\right)}\phi}\right)\times\boldsymbol{a}. \end{align}

Recalling (3.3), we see that the third term on the left-hand side of (3.7) arises from the curvature of the magnetic field. Terms involving ${\partial \phi }/{\partial z}$ describe the effect of the inhomogeneity of the electric potential along the vertical axis. The term including $\boldsymbol {\nabla }\times \boldsymbol {B}=\epsilon _B\boldsymbol {\nabla }\times \boldsymbol {a}$ can be ascribed to the presence of electric current in the system. Finally, the last term on the right-hand side results from the polarization drift associated with the component of the magnetic field $\epsilon _B\boldsymbol {a}$. Observe that (3.7) reduces to the Hasegawa–Mima equation when $\epsilon _B=0$:

(3.8)\begin{equation} \frac{\partial}{\partial t}\left({\lambda\phi-\frac{\sigma}{B_0^2}\Delta_{\left({x,y}\right)}\phi}\right)=\frac{\sigma}{B_0^3}\left[\phi,\Delta_{\left({x,y}\right)}\phi\right]_{\left({x,y}\right)}.\end{equation}

The effect of the field curvature (3.3) can be made explicit by expanding $\boldsymbol {a}$ in Taylor series around $z=0$, and by considering the dynamics on such a plane. At first order in $z$, one has

(3.9a,b)\begin{equation} \boldsymbol{a}=\boldsymbol{a}_0+z\boldsymbol{a}_1,\quad \boldsymbol{\kappa}=\frac{\epsilon_B}{B_0}\boldsymbol{a}_1, \end{equation}

where $\boldsymbol {a}_0=\left ({a_{0x},a_{0y},0}\right )$ and $\boldsymbol {a}_{1}=\left ({a_{1x},a_{1x},0}\right )$ are vector fields independent of $z$. Using (3.9a,b) and setting ${\partial \phi }/{\partial z}=0$, all terms in (3.7) lose the dependence on $z$, giving a two-dimensional equation:

(3.10)\begin{gather} \frac{\partial}{\partial t}\left( \lambda\phi-\frac{\sigma}{B_0^2}\Delta_{\left({x,y}\right)}\phi+\frac{\sigma}{B_0^2}\boldsymbol{\kappa}\boldsymbol{\cdot}\boldsymbol{\nabla}\phi \right)=\frac{\sigma}{B_0^3}\left[ \phi,\Delta_{\left({x,y}\right)}\phi \right]_{\left({x,y}\right)}\nonumber\\ -\frac{1}{B_0}\left({1-\frac{\sigma}{B_0^2}\Delta_{\left({x,y}\right)}\phi}\right)\boldsymbol{\kappa}\times\boldsymbol{\nabla}\phi\boldsymbol{\cdot}\boldsymbol{\nabla} z. \end{gather}

In many applications, the curvature of the magnetic field is not small. It is therefore instructive to examine how the Hasegawa–Mima equation is modified when curvature is a leading-order term. To this end, consider a circular magnetic field $\boldsymbol {B}= B_0 r\boldsymbol {\nabla }\varphi$, where $\left ({r,\varphi,z}\right )$ are cylindrical coordinates and $B_0\in \mathbb {R}$. Notice that $\boldsymbol {B}^2= B_0^2$ is constant (unlike the usual dependence $\left \lvert {\nabla \varphi }\right \rvert ^2=1/r^2$), and that the curvature of the magnetic field is given by $\boldsymbol {\kappa }=-\boldsymbol {\nabla }\log r$. Assuming that the condition (2.36), which in this case can be explicitly written as $r^{-1}\partial \left \lvert {\boldsymbol {\nabla }_{\perp }\phi }\right \rvert ^2/\partial z\sim \epsilon ^3$, is initially satisfied by the electric potential $\phi$, (2.39) can be written as

(3.11)\begin{equation} \frac{\partial}{\partial t}\left(\lambda\phi\!-\!\frac{\sigma}{ B_0^2}\Delta_{\left({z,r}\right)}\phi\right)\!=\! \frac{\kappa}{ B_0}\frac{\partial\phi}{\partial z}\left({\frac{\sigma}{ B_0^2}\Delta_{\left({z,r}\right)}\phi-1}\right)\!-\frac{\sigma\kappa}{ B_0^3 }\left[\phi,\frac{\partial\phi}{\partial r}\right]_{\left({z,r}\right)}+\frac{\sigma}{ B_0^3}\left[\phi,\Delta_{\left({z,r}\right)}\phi\right]_{\left({z,r}\right)}, \end{equation}

where we introduced the differential operators

(3.12a–c)\begin{align} \boldsymbol{\nabla}_{\left({z,r}\right)}f=\frac{\partial f}{\partial z}\boldsymbol{\nabla} z+\frac{\partial f}{\partial r}\boldsymbol{\nabla} r,\quad \Delta_{\left({z,r}\right)}f=\frac{1}{r}\frac{\partial}{\partial r}\left({r\frac{\partial f}{\partial r}}\right)+\frac{\partial^2 f}{\partial z^2},\quad \left[f,g\right]_{\left({z,r}\right)}\!=\frac{\partial f}{\partial z}\frac{\partial g}{\partial r}-\frac{\partial g}{\partial z}\frac{\partial f}{\partial r}. \end{align}

Notice that the field curvature modifies the Hasegawa–Mima equation through the modulus $\kappa ^2=1/r^2$, and that (3.11) is two-dimensional if axial symmetry $\partial \phi /\partial \varphi =0$ is assumed. Furthermore, since we expect the electric potential $\phi$, the electric field $-\boldsymbol {\nabla }_{\left ({z,r}\right )}\phi$ and the electric charge $-\Delta _{\left ({z,r}\right )}\phi$ to be bounded, the Hasegawa–Mima equation can be recovered in the limit $r\rightarrow \infty$ ($\kappa \rightarrow 0$) where field lines become progressively straight. Next, observe that in the Hasegawa–Mima equation (3.8) steady states are given by the equation $[\phi,\Delta _{\left ({x,y}\right )}\phi ]=0$, or simply $\Delta _{\left ({x,y}\right )}\phi =-f\left ({\phi }\right )$ with $f$ some function of $\phi$. Since the electric charge $-\Delta _{\left ({x,y}\right )}\phi$ should vanish when $\phi =0$, for small $\phi$ we may set $f=f_0\phi$ with $f_0$ a positive real constant (the positive sign physically means that charge density gradients $-\boldsymbol {\nabla }_{\left ({x,y}\right )}\Delta _{\left ({x,y}\right )}\phi$ are directed in the opposite direction to the electric field $-\boldsymbol {\nabla }_{\left ({x,y}\right )}\phi$). Then, considering a two-dimensional domain $\left ({x,y}\right )\in V=[0,{\rm \pi} ]^2$ such that the electric potential is grounded on the boundary, i.e. $\phi =0$ on $\partial V$, solution of the steady Hasegawa–Mima equation gives self-organized states of the type $\phi =\phi _0\sin \left ({m x}\right )\sin \left ({n y}\right )$ with $\phi _0\in \mathbb {R}$, $m,n\in \mathbb {Z}$ and $f_0=m^2+n^2$. Since $f_0$ corresponds to the ratio between enstrophy and energy in the fluid limit $\lambda =0$, at equilibrium the minimum possible value $f_0=2$ corresponding to $m=n=1$ is expected to be preferentially selected (see e.g. Hasegawa (Reference Hasegawa2004) on this point). Let us see how the situation changes in a curved magnetic field. Since the right-hand side of (3.11) can be written as

(3.13)\begin{equation} \frac{1}{r}\left[\phi,-\frac{r}{ B_0}-\frac{\sigma}{ B_0^3}\frac{\partial\phi}{\partial r}+\frac{\sigma }{ B_0^3}r\Delta_{\left({z,r}\right)}\phi\right]_{\left({z,r}\right)}, \end{equation}

steady states in the circular magnetic field $\boldsymbol {B}= B_0 r\boldsymbol {\nabla }\phi$ are described by the equation

(3.14)\begin{equation} \frac{\sigma}{ B_0^3}\left({\frac{\partial^2\phi}{\partial r^2}+\frac{\partial^2\phi}{\partial z^2}}\right)=\frac{1}{ B_0}-\frac{f\left({\phi}\right)}{r}. \end{equation}

Considering the case $f=f_0\phi$ and taking a two-dimensional toroidal domain with squared cross-section $\left ({r,z}\right )\in V=[1,2]^2$ and Dirichlet boundary conditions $\phi =0$ on the boundary $\partial V$, solution of (3.14) results in a self-organized steady state sustained by the curvature of the magnetic field. Figure 1 shows contour plots of the steady electric potential $\phi$ and vorticity $\omega =\boldsymbol {\nabla }\times \boldsymbol {v}\boldsymbol {\cdot } r\boldsymbol {\nabla }\varphi$ with $\boldsymbol {v}$ given by (2.41) obtained by numerical solution of (3.14) as compared with the Hasegawa–Mima case. The corresponding fluid drifts $\boldsymbol {v}_{\boldsymbol {E}}$ and $\boldsymbol {v}$ are given in figure 2. From these figures, one sees that contours of electric potential $\phi$, vorticity $\omega$ and fluid drifts $\left \lvert {\boldsymbol {v}_{\boldsymbol {E}}}\right \rvert$ and $\left \lvert {\boldsymbol {v}}\right \rvert$ tend to accumulate in regions of higher curvature (small radius $r$), implying the onset of steeper gradients, while inhomogeneities are suppressed where the curvature is weaker. Figure 2 also reveals that the fluid drifts $\boldsymbol {v}_{\boldsymbol {E}}$ and $\boldsymbol {v}$ are enhanced where the curvature is stronger. We remark that the observed behaviour is not caused by the gradient or curvature drifts of the guiding centre framework because the cold ions approximation is being considered. In addition, the background magnetic field has uniform strength in this example. Hence, curvature affects self-organized states through the $\boldsymbol {E}\times \boldsymbol {B}$ drift, as clear from (2.39).

Figure 1. (a,b) Contour plots of the self-organized steady electric potential $\phi$ in a straight magnetic field $\boldsymbol {B}=B_0\boldsymbol {\nabla } z$ (Hasegawa–Mima equation) and in a circular magnetic field $\boldsymbol {B}= B_0 r\boldsymbol {\nabla }\varphi$. (c,d) Contour plots of the respective vorticities $\omega =\boldsymbol {\nabla }\times \boldsymbol {v}\boldsymbol {\cdot }\boldsymbol {\nabla } z$ and $\omega =\boldsymbol {\nabla }\times \boldsymbol {v}\boldsymbol {\cdot } r\boldsymbol {\nabla }\varphi$ with the ion fluid velocity $\boldsymbol {v}$ defined by (2.41). In this simulation, $B_0=1$ and $f_0=2$ for the Hasegawa–Mima case, while $B_0=1$, $\sigma =0.1$ and $f_0=1$ for the circular magnetic field case.

Figure 2. (a,b) Vector plots of the $\boldsymbol {E}\times \boldsymbol {B}$ drift velocity $\boldsymbol {v}_{\boldsymbol {E}}$ associated with the steady states of figure 1 and contour plots of the modulus $\left \lvert {\boldsymbol {v}_{\boldsymbol {E}}}\right \rvert$. (c,d) Vector plots of the corresponding total ion fluid velocity $\boldsymbol {v}$ of (2.41) and contour plots of the modulus $\left \lvert {\boldsymbol {v}}\right \rvert$.

The effect of vertical inhomogeneity in the potential $\phi$ can be further examined by setting $\phi =q+\sin \left ({m z}\right )p$, with $q\left ({r}\right )$ and $p\left ({r}\right )$ radial functions and $m\in \mathbb {Z}$. Then, (3.14) reduces to the system

(3.15a,b)\begin{equation} \frac{\sigma}{ B_0^3}\frac{\partial^2 p}{\partial r^2}+\left({\frac{f_0}{r}-m^2\frac{\sigma}{ B_0^3}}\right)p=0,\quad \frac{\sigma}{ B_0^3}\frac{\partial^2 q}{\partial r^2}+\frac{f_0}{r}q-\frac{1}{ B_0}=0. \end{equation}

A plot of the electric potential $\phi$ obtained by solution of system (3.15a,b) for different values of $m$ and $B_0$ is given in figure 3. Notice that for a sufficiently large magnetic field strength $B_0$, structures arise in the radial direction as well. The size and spacing of these radial structures appear to be modulated by the background strength and curvature of the magnetic field rather than the constant $m$ associated with the vertical oscillation.

Figure 3. Contour plots of the electric potential $\phi$ obtained by solution of (3.15a,b) for different values of $m$ and $B_0$. Dirichlet boundary conditions $p(1)=p(2)=1$ and $q(1)=q(2)=1$ are used. The case $m=1$ for (a) $B_0=1$ and (d) $B_0=5$. The case $m=3$ for (b) $B_0=1$ and (e) $B_0=5$. The case $m=6$ for (c) $B_0=1$ and (f) $B_0=5$. In this simulation $\sigma =0.5$ and $f_0=1$.

4. The case of curved magnetic fields crossing a surface perpendicularly

The Hasegawa–Mima equation is endowed with two inviscid invariants, the total energy and the generalized enstrophy. The generalized enstrophy is an invariant arising from the two-dimensional nature of the governing equation, which is restricted to the flat $\left ({x,y}\right )$ plane with normal given by the straight vertical magnetic field $\boldsymbol {B}=B_0\boldsymbol {\nabla } z$. It is useful to consider the conditions under which the same kind of topological invariant persists in general magnetic fields. A condition for the analogy with two-dimensional vorticity dynamics to apply is that the magnetic field defines the normal direction of a general (not necessarily flat) two-dimensional surface $\varSigma \subset \mathbb {R}^3$. In this case, the dynamics is restricted to the surface $\varSigma$ because the drift velocity (2.23) satisfies $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {v}=0$. The geometric condition for a vector field $\boldsymbol {B}$ to locally define the normal of a surface $\varSigma$ is given by the Frobenius integrability condition (Frankel Reference Frankel2012):

(4.1)\begin{equation} \boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{\nabla}\times\boldsymbol{B}=0. \end{equation}

In particular, if the magnetic field $\boldsymbol {B}$ has vanishing helicity density then there exist locally defined functions $\alpha,C$ such that

(4.2)\begin{equation} \boldsymbol{B}=\alpha\boldsymbol{\nabla} C. \end{equation}

The magnetic field $\boldsymbol {B}$ thus defines the normal to the surface $C={\rm constant}$. When $\alpha =\alpha \left ({C}\right )$, the magnetic field $\boldsymbol {B}$ becomes a vacuum magnetic field because $\boldsymbol {\nabla }\times \boldsymbol {B}=\boldsymbol {0}$. In this section, we are concerned with magnetic fields of the type (4.2). We will assume that the functions $\alpha$ and $C$ exist in the domain $V$, and that $\boldsymbol {B}\neq \boldsymbol {0}$ in $V$. It is worth noticing that for time-independent magnetic fields the constraint (4.1) corresponds to the requirement that the electric current $\boldsymbol {J}=\boldsymbol {\nabla }\times \boldsymbol {B}$ is always perpendicular to the magnetic field, $\boldsymbol {J}\boldsymbol {\cdot }\boldsymbol {B}=0$. In tokamaks this condition will be rarely satisfied because most of the plasma current is aligned with the magnetic field. In addition, we remark that adiabatic electron response underlying the generalized Hasegawa–Mima equation (2.39) may impose additional constraints on the magnetic field configuration. Indeed, one expects adiabatic electron response to hold only when the integral curves of the magnetic field form closed surfaces, with generally non-rational rotational transform.

Next, recall that the magnetic field $\boldsymbol {B}$ must be solenoidal. Hence, the Lie–Darboux theorem (Arnold Reference Arnold1989; de Léon Reference de Léon1989) applies: locally there exist functions $\varPsi,\theta$ such that

(4.3)\begin{equation} \boldsymbol{B}=\boldsymbol{\nabla}\varPsi\times\boldsymbol{\nabla}\theta. \end{equation}

Again, we will assume that the functions $\varPsi$ and $\theta$ are well defined in the domain $V$. A typical example of vacuum magnetic field is the magnetic field generated by a point dipole. In this case

(4.4a–d)\begin{equation} \alpha=1,\quad C={-}M\frac{z}{\left({r^2+z^2}\right)^{3/2}},\quad \varPsi=M\frac{r^2}{\left({r^2+z^2}\right)^{3/2}},\quad \theta=\varphi, \end{equation}

where $\left ({r,\varphi,z}\right )$ are cylindrical coordinates and $M$ a physical constant with units of T m$^3$. The functions $\left ({C,\varPsi,\theta }\right )$ can be used as a system of curvilinear coordinates. The Jacobian determinant of the coordinate transformation is given by

(4.5)\begin{equation} J=\boldsymbol{\nabla} C\boldsymbol{\cdot}\boldsymbol{\nabla}\varPsi\times\boldsymbol{\nabla}\theta=\frac{B^2}{\alpha}. \end{equation}

Given two functions $f,g$ it is convenient to introduce the bracket

(4.6)\begin{equation} \left[f,g\right]_{\left({\varPsi,\theta}\right)}=\frac{\partial f}{\partial\varPsi}\frac{\partial g}{\partial\theta}- \frac{\partial f}{\partial\theta}\frac{\partial g}{\partial\varPsi}.\end{equation}

Using (4.6), the derived (2.39) can be written as

(4.7)\begin{equation} \frac{\partial}{\partial t}\left[\lambda\phi-\sigma\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}}\right)\right]=\frac{B^2}{\alpha}\left[\phi, -\frac{\alpha}{B^2} +\sigma\frac{\alpha^2}{B^4}\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{\boldsymbol{\nabla}_{{\perp}}\phi}{\alpha}}\right) \right]_{\left({\varPsi,\theta}\right)}. \end{equation}

One can verify that under appropriate boundary conditions on the surface boundary $\partial \varSigma$ the surface energy

(4.8)\begin{equation} H_{\varSigma}=\frac{1}{2}\int_{\varSigma}\left({\lambda\phi^2+\sigma\frac{\left\lvert{\boldsymbol{\nabla}_{{\perp}}\phi}\right\rvert^2}{B^2}}\right)\frac{\alpha}{B^2}\,{\rm d}\varPsi \,{\rm d}\theta \end{equation}

is a constant of (4.7). The condition for conservation of generalized enstrophy,

(4.9)\begin{equation} W_{\varSigma}=\frac{1}{2}\int_{\varSigma}\left\{ \lambda\frac{\left\lvert{\boldsymbol{\nabla}_{{\perp}}\phi}\right\rvert^2}{B^2}+\sigma\left[\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{\boldsymbol{\nabla}_{{\perp}}\phi}{B^2}}\right)\right]^2 \right\}\frac{\alpha}{B^2}\,{\rm d}\varPsi \,{\rm d}\theta,\end{equation}

can be obtained by noting that the second argument of the bracket on the right-hand side of (4.7) must be a function of $\boldsymbol {\nabla }\boldsymbol {\cdot }\left ({B^{-2}\boldsymbol {\nabla }_{\perp }\phi }\right )$ up to a function of $\phi$. The condition is

(4.10)\begin{equation} \alpha=\frac{k}{\left\lvert{\boldsymbol{\nabla} C}\right\rvert^2}=\frac{B^2}{k},\quad k\in\mathbb{R},\end{equation}

which is equivalent to

(4.11)\begin{equation} \boldsymbol{\nabla}\times\left({\frac{\boldsymbol{B}}{B^2}}\right)=\boldsymbol{0}. \end{equation}

In this case, $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v}_{\boldsymbol {E}}=\boldsymbol {\nabla }\phi \boldsymbol {\cdot }\boldsymbol {\nabla }\times \left ({B^{-2}\boldsymbol {B}}\right )=0$. Notice also that $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}=0$ implies that configurations of the type (4.10) must satisfy

(4.12)\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot}\left({\frac{\boldsymbol{\nabla} C}{\left\lvert{\boldsymbol{\nabla} C}\right\rvert^2}}\right)=0.\end{equation}

In spherical geometry, denoting with $R$ the spherical radius, a magnetic field satisfying (4.10) and (4.12) can be obtained by setting

(4.13a–c)\begin{equation} \alpha=\frac{ B_0}{R^4},\quad B_0\in\mathbb{R},\quad C=\frac{R^3}{3}. \end{equation}

Similarly, in cylindrical geometry, magnetic fields compatible with (4.10) and (4.12) include those generated by

(4.14a)\begin{align} \alpha& =\frac{ B_0}{r^2},\quad B_0\in\mathbb{R},\quad C=\frac{r^2}{2}, \end{align}

(4.14b)\begin{align} \alpha& = B_0 r^2,\quad B_0\in\mathbb{R},\quad C=\varphi. \end{align}

Observe that when $\lambda =0$ (4.7) with either (4.13a–c) or (4.14a) gives the usual two-dimensional vorticity dynamics on a sphere or cylinder respectively. The case of (4.14b) corresponds to a circular magnetic field $\boldsymbol {B}= B_0 r^2\boldsymbol {\nabla }\varphi$ with curvature $\boldsymbol {\kappa }=-\boldsymbol {\nabla }\log r$. Assuming axial symmetry $\phi =\phi \left ({r,z}\right )$, the corresponding form of (2.39) is again two-dimensional:

(4.15)\begin{equation} \frac{\partial}{\partial t}\left[\lambda\phi-\frac{\sigma}{ B_0^2}\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\kappa^2\boldsymbol{\nabla}_{\left({z,r}\right)}\phi}\right)\right]= \frac{\sigma}{ B_0^3}\kappa\left[\phi,\boldsymbol{\nabla}\boldsymbol{\cdot}\left({\kappa^2\boldsymbol{\nabla}_{\left({z,r}\right)}\phi}\right)\right]_{\left({z,r}\right)}. \end{equation}

5. Concluding remarks

In conclusion, we have derived a model equation (2.39) describing electrostatic plasma turbulence in a general magnetic field. The equation preserves the mass (2.28) and the energy (2.33), and reduces to the Hasegawa–Mima equation in the limit of a straight magnetic field. The ordering adopted in the derivation of the equation is slightly different from the classical one. On the one hand, both the magnetic field and the electrostatic potential are allowed to vary on the same spatial scale. On the other hand, the requirement (2.36), which is automatically satisfied in the standard setting of the Hasegawa–Mima equation, ensures the consistency of the ordering with respect to preservation of energy. This latter condition implies that the derived equation is best suited for magnetic fields satisfying (2.37), implying a second-order $\boldsymbol {E}\times \boldsymbol {B}$ drift velocity divergence, or for spatial scales such that the change in $\boldsymbol {v}_{\boldsymbol {E}}^2$ represents a third-order contribution (2.38). Nevertheless, as discussed at the end of § 2 the same (2.39) can be obtained from the standard ordering, at the price of more stringent constraints on the spatial behaviour of the magnetic field.

Conservation of generalized enstrophy holds when the magnetic field defines the normal of a surface and it is compatible with two-dimensional vorticity dynamics. It should be noted that inverse energy cascades are expected to occur for all magnetic configurations such that generalized enstrophy is constant. Indeed, the order of $\phi$ derivatives appearing in (4.8) and (4.9) is not changed by the geometry of the background magnetic field. Detailed analysis of the effect of magnetic topology on inverse cascades and zonal flows is left for future work.

As a physical application of the obtained equation, we have studied how the curvature of a circular magnetic field with uniform strength modifies self-organized steady states by comparison with analogous equilibria in a straight magnetic field. A strong curvature tends to attract level sets of electric potential and vorticity, and to enhance fluid drift velocity. A higher curvature also appears to contribute to higher heterogeneity in the electric potential. This behaviour cannot be ascribed to gradient and curvature drifts occurring in the guiding centre picture because the model relies on the cold ions approximation. Hence, the effect of curvature is mediated by the $\boldsymbol{E}\times \boldsymbol{B}$ drift.

Finally, the results reported in this paper may be useful for constructing simplified models of turbulence in complex plasma systems of practical interest. In particular, we expect the derived equation to serve as a toy model of turbulence in tokamak and stellarator plasmas.