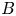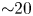1 Introduction
Electron holes are nonlinear solitary BGK (Bernstein, Greene & Kruskal Reference Bernstein, Greene and Kruskal1957) electrostatic structures sustained by electron trapping (Hutchinson Reference Hutchinson2017), which occur widely in space plasmas. For a recent summary of observations, see e.g. Lotekar et al. (Reference Lotekar, Vasko, Mozer, Hutchinson, Artemyev, Bale, Bonnell, Ergun, Giles and Khotyaintsev2020) and references therein. The theoretical stability of electron holes to motions with sinusoidal variation transverse to a magnetic field has recently been extensively analysed assuming that the relevant unstable perturbation is a parallel, kink-like, uniform shift of the hole position (Hutchinson Reference Hutchinson2018a,Reference Hutchinsonb, Reference Hutchinson2019a,Reference Hutchinsonb). In that work the dispersion relation's complex frequency 
$\omega$ was found using a ‘Rayleigh quotient’ (Parlett Reference Parlett1974) which provides an approximation accurate to second order in any deviations from the exact unstable mode structure, and is equivalent to solving the hole's overall momentum balance (Hutchinson & Zhou Reference Hutchinson and Zhou2016). The results are in reasonable agreement with particle-in-cell (PIC) simulations, but some discrepancies have been noted. The purpose of the present work is to discover whether more accurate mode parallel shape determination, including deviations from the shiftmode, can explain those discrepancies, and to quantify by analysis how important the deviations are.
Two main phenomena have been observed in transverse instability PIC simulations that are not well represented by the shiftmode analysis. They are (1) narrowing of the unstable mode structure relative to the shiftmode when near marginal oscillatory stability (Hutchinson Reference Hutchinson2019b) and (2) generation of long parallel length external ‘streaks’ or waves on the whistler branch during oscillatory instability at high magnetic field (Hutchinson Reference Hutchinson2019a).
Our approach to managing a generalization of the unstable mode of a Vlasov–Poisson problem, following long-standing mathematical analysis (Lewis & Symon Reference Lewis and Symon1979; Symon, Seyler & Lewis Reference Symon, Seyler and Lewis1982), is to represent the perturbation of potential in terms of the orthogonal eigenmodes of a judiciously chosen differential operator. In the present context, the operator generally used (Lewis & Seyler Reference Lewis and Seyler1982) represents the Poisson equation for steady (or very slowly varying) potential (
$\nabla ^2\phi -n=0$ in appropriately normalized units). The charged particle density difference 
$n_0(z)$ associated with the potential equilibrium 
$\phi _0(z)$ can be determined from this equation. Then for infinitesimally slow linearized potential perturbations 
$\phi _1$ about this equilibrium, the perturbed density is 
$n_1=\phi _1\,{\rm d}n_0/{\rm d}\phi _0$, and the resulting Poisson equation can be written using the operator 
$V_a \equiv (\nabla ^2-{\rm d}n_0/{\rm d}\phi _0)$ acting on 
$\phi _1$ as 
$V_a\phi _1=0$. This 
$V_a$ is called the ‘adiabatic’ operator, and the associated density perturbation 
$n_1$ the adiabatic density (perturbation). For low frequencies, expansion of the potential perturbation is most naturally in terms of the eigenmodes of 
$V_a$. For purely growing instabilities 
$\omega =0+{\rm i}\omega _i$, at the threshold 
$\omega _i\sim 0$, evidently the adiabatic response is nearly equal to the total because changes are infinitesimally slow; so the non-adiabatic part 
$\tilde V$ of the operator is small compared with 
$V_a$ in the perturbed Poisson equation. Consequently to lowest order the perturbation-unstable mode is equal to the eigenmode of 
$V_a$ with zero eigenvalue. For a solitary potential structure in a uniform background, such a zero eigenvalue always exists, and its eigenmode has the form of a uniform shift of the equilibrium.
By the preceding argument, determining where 
$\omega _i=0$, i.e. the stability threshold, can be accomplished exactly using just the shiftmode, provided that the real part 
$\omega _r$ of the mode frequency is zero. However, some hole instabilities are oscillatory, 
$\omega _r\neq 0$, 
$\omega _i>0$, and even if they are not we may wish to find a finite 
$\omega _i$ value. Then the unstable mode is not purely the shiftmode, and the extent to which it includes contributions from other eigenmodes of 
$V_a$ becomes an important question. It can be explored by carrying the perturbation analysis to first order in the other eigenmodes, in much the way that time-independent perturbation theory is used in quantum mechanics. This approach was successfully pursued in an early study of the one-dimensional instability of a train of electron holes that leads eventually to hole merger (Schwarzmeier et al. Reference Schwarzmeier, Lewis, Abraham-Shrauner and Symon1979). However, the few subsequent efforts to apply it (Schamel Reference Schamel1982, Reference Schamel1987; Collantes & Turikov Reference Collantes and Turikov1988) have been of limited utility either because of expanding about the wrong eigenmode (symmetric and not having zero eigenvalue) or, more fundamentally, because of adopting inappropriate approximations to the solution of the Vlasov equation (Jovanović & Schamel Reference Jovanović and Schamel2002), which constitutes the complementary (and more difficult) part of the Poisson–Vlasov system: the non-adiabatic perturbation. A more recent one-dimensional analysis (Dokgo et al. Reference Dokgo, Woo, Choi, Min and Hwang2016) of 
${\,{\rm sech}}^2(z/\ell )$ shaped holes considered their sole antisymmetric discrete adiabatic eigenmode, which is simply the shiftmode.
A separate thread of this question is the coupling, observed in simulations (Oppenheim, Newman & Goldman Reference Oppenheim, Newman and Goldman1999; Oppenheim et al. Reference Oppenheim, Vetoulis, Newman and Goldman2001; Lu et al. Reference Lu, Lembege, Tao and Wang2008), of hole instabilities at high magnetic field to long-wavelength external perturbation ‘streaks’ identified as belonging to the cold plasma whistler branch. Previous analyses (Newman et al. Reference Newman, Goldman, Spector and Perez2001; Vetoulis & Oppenheim Reference Vetoulis and Oppenheim2001; Berthomier et al. Reference Berthomier, Muschietti, Bonnell, Roth and Carlson2002) theorized that coupling to these waves was the primary cause of instability at high field, but adopted unjustified ad hoc expressions for the coupling. Recently it was shown that the high-field instability is not explicitly caused by the coupling (Hutchinson Reference Hutchinson2019a), but since simulations show that external coupling can affect the instability, an interesting question remains as to how to calculate it self-consistently.
The present approach solves the Vlasov problem without expansion, by integration over the prior orbit, numerically in the hole region. In the process the solution for wave coupling emerges rigorously from the mathematical analysis. Moreover we avoid any perturbative approximation for the relative amplitudes of the different modes. Instead we show how, in addition to a single extra discrete eigenmode contribution, the eigenmode continuum contribution can be approximately represented through a single amplitude corresponding to the external wave dispersion relation. Section 2 explains the eigenmodes and the expansion. Section 3 shows for the Vlasov operator form how the continuum modes can be included and reduced to effectively a single contribution. Section 4 discusses the numerical and analytic evaluations needed. Section 5 presents results.
Prior analysis has been, like the present work, of linearized stability. The nonlinear consequences, observed in simulations, are generally that the holes break up, becoming of limited transverse extent and of reduced amplitude. The resulting three-dimensional holes can, it seems, become stable because the unstable wavenumber modes do not fit within their transverse extent. However, nonlinear hole breakup is beyond the present scope.
2 Eigenmode expansion
Let us adopt a minimalist bra–ket notation for the adiabatic eigenmodes in which we expand 
$|e\rangle$, where the label 
$e$ being either real 
$p,q,\dots$ or integer 
$j,l,\ldots$ will denote respectively continuum or discrete eigenmodes. The inner product of any two Hilbert-space vectors (complex potential functions of 
$z$) denotes an overlap integral over (parallel) spatial coordinate 
$\langle u |s\rangle \equiv \int u^*(z)s(z)\,{\rm d}z$. Insofar as the eigenmodes are orthonormal, we write 
$\langle u |s\rangle =\delta _{us}$, where for continuum modes such that 
$u$ and 
$s$ are real parameters this is (approximately) a Dirac delta function, 
$\delta _{us}=\delta (u-s)$, whereas for discrete modes 
$\delta _{jl}$ is the Kronecker delta.
2.1 Adiabatic response eigenmodes
In units scaled to Debye length, electron background density and electron thermal energy, the one-dimensional Poisson equation, assuming immobile uniform ion density, is 
${\rm d}^2\phi /{\rm d}z^2=n-1$. The equilibrium analysed is chosen to be of the form 
$\phi _0=\psi {\,{\rm sech}}^4(z/4)$. Writing for brevity 
$S={\,{\rm sech}}(z/4)$ and 
$T=\tanh (z/4)$ and denoting the 
$z$ derivative by prime, the linearized equilibrium (‘adiabatic’) Poisson operator for this hole potential can then be written
\begin{equation} V_a = \left[\frac{{\rm d}^2}{{\rm d}z^2} - \frac{{\rm d}n}{{\rm d}\phi_0}\right] = \left[\frac{{\rm d}^2}{{\rm d}z^2} - \frac{\phi_0^{'''}}{\phi_0'}\right] = \left[\frac{{\rm d}^2}{{\rm d}z^2} +\frac{30}{16}S^2- 1\right]. \end{equation}
Notation 
$V$ reminds us that this is partly the Vlasov operator, transforming a potential into a density, and the subscript 
$a$ denotes adiabatic (meaning steady). The eigenmodes of this operator, satisfying 
$V_a|u\rangle =\lambda |u\rangle$, can be found (see Appendix A) by applying the raising operator 
$4 ({{\rm d}}/{{\rm d}z})-l T$ for 
$l=1,2,3,4,5$ to the function 
${\rm e}^{uz/4}$ yielding
$$\begin{gather} |u\rangle(z)= \exp(uz/4)\{[{-}15u^4 + (420S^2 - 225)u^2 - 945S^4 + 840S^2 - 120]T \nonumber\\ +\, u[u^4 + ({-}105S^2 + 85)u^2 + (945S^4 - 1155S^2 +274)]\}. \end{gather}$$
For real 
$u$, as 
$u z\to +\infty$ the mode is bounded (and tends to zero) only if 
$u$ is one of the discrete roots of the polynomial in the braces obtained by letting 
$S\to 0$ and 
$T\to {\rm sign}(u)$. These are 
$u=j=1,2,3,4,5$. The odd-numbered discrete modes are symmetric in 
$z$, and the even-numbered are antisymmetric. In contrast, imaginary 
$u$ values 
$u={\rm i}p$ give rise to the continuum modes which are formally finite at infinity. Their overlap integral over a finite domain exists; and, as the domain tends to infinity, it tends to a delta function. The continuum eigenmodes have definite parity only if 
$u$ reverses sign with 
$z$; so we write 
$u={\rm i} \sigma _z p$, where 
$\sigma _z={\rm sign}(z)$ and positive 
$p$ represents antisymmetric outwardly propagating waves.
The corresponding eigenvalues are
\begin{equation} \lambda_u= u^2/16-1={-}p^2/16-1. \end{equation}
Normalized so that 
$\langle j |l\rangle =\delta _{jl}$, they are given in table 1.
Table 1. Discrete eigenmodes.
In particular 
$\lambda _4=0$ for the shiftmode 
$|4\rangle \propto {\rm d}\phi _0/{\rm d}z$, and it is the predominant perturbation in essentially all linear electron hole instabilities. Moreover, it couples only to antisymmetric modes; so 
$|2\rangle$ is the only other discrete mode that needs to be considered.
It can be shown that the the continuum modes are ‘normalized’, in the sense that then 
$\langle p |q\rangle =\delta _{pq}=\delta (p-q)$, by dividing (2.2) by the factor
\begin{equation} [8{\rm \pi}(p^2+1^2)(p^2+2^2)(p^2+3^2)(p^2+4^2)(p^2+5^2)]^{1/2}. \end{equation}
Far from the hole (
$|z|\gg 1$) the normalized oscillatory continuum modes are sinusoidal with amplitude 
$1/\sqrt {8{\rm \pi} }=0.19947$ and parallel wavenumber 
$|k_\parallel |=p/4$. The eigenmodes are plotted in figure 1.
Figure 1. Eigenmodes of the adiabatic response operator.
2.2 Including non-adiabatic response
We now must consider the full linearized Poisson equation including the non-adiabatic response arising from the solution to the time-dependent Vlasov equation, 
$\tilde {V}$, as well as the adiabatic response 
$V_a$. The form of the non-adiabatic Vlasov operator 
$\tilde {V}$ is discussed later. For a perturbation 
$\phi _1(y,z,t)=\hat \phi (z)\exp ({{\rm i}(k_\perp y-\omega t)})$ with transverse wavenumber 
$k_\perp$ and frequency 
$\omega$, Poisson's equation becomes
\begin{equation} ({-}k_\perp^2+V_a+\tilde{V})|\hat\phi\rangle=0, \end{equation}
in which it is convenient to regard 
$k_\perp ^2\equiv \lambda _\perp$ as the full eigenvalue. We suppose the solution for potential can be expanded as a sum of scalar amplitudes 
$a_u$ times the eigenmodes 
$|u\rangle$ of 
$V_a$:
\begin{equation} |\hat\phi\rangle=\sum_u a_u |u\rangle, \end{equation}where the summation notation also includes an integral over the continuum modes.
Then we can invoke the orthogonal properties of the adiabatic eigenmodes and form the inner product:
\begin{equation} \langle s|( V_a+\tilde{V})|\hat\phi\rangle = \lambda_s\langle s|s\rangle a_s+\sum_u\langle s|\tilde{V}|u\rangle a_u, \end{equation}
which must be equal to 
$\lambda _\perp \langle s |s\rangle a _s$ to satisfy (2.5). In particular, choosing the predominant mode 
$\langle 4|$ for 
$\langle s |$, for which 
$\lambda _4=0$, we get an eigenvalue equation 
$0=(\lambda _4-\lambda _\perp )\langle 4|4\rangle a _4+\sum _u\langle 4|\tilde {V}|u\rangle a _u$.
If all the amplitudes 
$a_u$ for 
$u\neq 4$ are negligible, then 
$\tilde {V}$ contributes a correction (
$\lambda _{4}^{(1)}$) to the eigenvalue:
\begin{equation} \lambda_{4}^{(1)}= \frac{\langle4|\tilde{V}|4\rangle}{\langle4|4\rangle}=\lambda_\perp{-}\lambda_4. \end{equation}
The expression 
$\langle 4|\tilde {V}|4\rangle /\langle 4|4\rangle$ is the ‘Rayleigh quotient’ approximation for the eigenvalue of 
$V_a+\tilde {V}$ (because 
$\lambda _4=0$). It is physically the (normalized) jetting force on particles because of the unperturbed electric field 
$-{\rm d}\phi _0/{\rm d}z\propto \langle 4|$, acting on the non-adiabatic density perturbation 
$\tilde n = \tilde {V}|4\rangle$, integrated over the entire hole. It balances the (normalized) Maxwell shear stress from the transverse kinking of the hole (
$k_\perp ^2$) to make the total force zero.
Actually 
$\tilde {V}$ is a complicated nonlinear function of the complex frequency 
$\omega$ of the mode; and for specified 
$k_\perp$ the dispersion relation between 
$\omega$ and 
$k_\perp$ must be solved by some kind of iterative procedure searching for an 
$\omega$ that satisfies (2.8). The imaginary part of 
$\omega$ thus found determines the stability of the hole. This approximation has yielded stability results (Hutchinson Reference Hutchinson2018b, Reference Hutchinson2019a,Reference Hutchinsonb) that are in reasonable (but not perfect) agreement with simulation. The question at hand is whether analysis can determine approximately the magnitude of the other coefficients 
$a_u$ for 
$u\neq 4$, and therefore give a more accurate perturbation structure 
$|\hat \phi \rangle$ and 
$\omega$.
If instead of the approximation (2.8) we are able to evaluate all the matrix coefficients 
$\langle s |\tilde {V}|u\rangle$, then in principle we can regard (2.7) instead of (2.8) as a matrix eigensystem we must solve to find the 
$\omega$ that permits a non-zero solution for the vector 
$a_u$. The off-diagonal matrix entries 
$s\neq u$ are the coupling of the potential modes by the non-adiabatic Vlasov operator 
$\tilde {V}$. The condition for the existence of a solution is that the determinant of the matrix 
$[(-\lambda _\perp +\lambda _s)\langle s |s\rangle \delta _{su}+\langle s |\tilde {V}|u\rangle ]$ should be zero.
Such a programme faces formidable practical challenges, however, because each evaluation of 
$\tilde {V}|u\rangle$ requires a computation involving multiple-dimension integrations over space and velocity distribution – repeated for each mode 
$|u\rangle$ and each adjustment of 
$\omega$. Moreover, in principle, the continuum contains infinitely many modes, and the matrix contains the square of the number of modes. Obviously we require this number to be reduced. We can immediately restrict our attention just to antisymmetric modes, since by assumed symmetry no coupling to symmetric modes occurs. We later show how the entire continuum contribution can be reduced to a single amplitude. Continuum modes 
$|p\rangle$ extend to 
$|z|=\infty$, an integration range that for computation needs to be reduced, and have formally divergent inner products. We show how these difficulties are negotiated.
Formally, any mode for which 
$\tilde {V}|u\rangle a _u$ is not negligible must be retained in the sum of 
$\langle s |\tilde {V}|u\rangle$ in (2.7), giving for the dominant mode
\begin{equation} 0=(\lambda_4-\lambda_\perp)\langle4|4\rangle a_4+\langle4|\tilde{V}|4\rangle a_4+\sum_{u\neq 4}\langle4|\tilde{V}|u\rangle a_u, \end{equation}
but also for 
$s\neq 4$
\begin{equation} 0=(\lambda_s-\lambda_\perp)\langle s|s\rangle a_s+\langle s|\tilde{V}|4\rangle a_4+\sum_{u\neq 4}\langle s|\tilde{V}|u\rangle a_s. \end{equation} The well-known approach of time-independent perturbation theory in elementary quantum mechanics (see e.g. Dirac Reference Dirac1958, § 43) regards 
$\tilde {V}$ as systematically small, and takes 
$a_s$ for 
$s\neq 4$ also to be first-order small relative to 
$a_4$. The first-order approximation of (2.10) then drops the final sum term, giving
\begin{equation} a_s \simeq \frac{\langle s|\tilde{V}|4\rangle a_4}{(\lambda_\perp{-}\lambda_s)\langle s|s\rangle}. \end{equation}
Substituting back (with 
$s\to u$) into (2.9), the eigenvalue to second order is
\begin{equation} \lambda_\perp\simeq \lambda_4+\lambda_{4}^{(1)}+\lambda_{4}^{(2)}=\lambda_4 +\frac{\langle4|\tilde{V}|4\rangle}{\langle4|4\rangle} +\sum_{u\neq 4} \frac{\langle4|\tilde{V}|u\rangle\langle u|\tilde{V}|4\rangle}{(\lambda_\perp{-}\lambda_u)\langle4|4\rangle\langle u|u\rangle}. \end{equation}
Normally the substitution 
$\lambda _\perp \simeq \lambda _4$ is made in the final sum; but we do not need to do that since we consider 
$\lambda _\perp$ to be given and 
$\omega$ to be changed to achieve equality in this equation.
These perturbation equations (2.11) and (2.12) are appropriate for coupled discrete modes 
$|j\rangle$ when the amplitudes 
$a_u\langle u |u\rangle$ for 
$u\neq 4$ are small compared with 
$a_4\langle 4|4\rangle$. Those equations give the first-order mode amplitude and second-order eigenvalue correction from them. However, in our case, for the continuum modes, 
$\tilde {V}$ is not systematically small everywhere, and an altered approach appropriate to the actual form of 
$\tilde {V}$ must be adopted. We shall see that in order to obtain converged integrals for the relevant continuum inner products it is necessary to use the difference between 
$\tilde V |q\rangle$ and a pure wave operator expression 
$\tilde V_w|q\rangle$.
3 The eigenmode coefficients
3.1 The non-adiabatic linearized Vlasov operator
The operator 
$\tilde {V}$ transforms a potential perturbation 
$|u\rangle$ into a non-adiabatic density perturbation 
$\tilde n$, both of which are complex functions of 
$z$. It does so by solving the linearized time-dependent Vlasov equation for the non-adiabatic distribution function perturbation 
$\tilde f(z,v)$ and integrating it: 
$\tilde n =\int \tilde f \,{\rm d}v$. The solution can be found in terms of an integral over past time along the linearized Vlasov equation's ‘characteristic’, that is, the unperturbed orbit 
$\boldsymbol x(t)$, giving an integral expression
\begin{equation} \varPhi(\boldsymbol x,\boldsymbol v,t)\equiv \int_{-\infty}^t \phi_1(\boldsymbol x(\tau),t-\tau ) \,{\rm d}\tau, \end{equation}
where 
$\phi _1(\boldsymbol x,t)$ is the potential perturbation and 
$\boldsymbol x(\tau )$ is the past position of the unperturbed orbit that has velocity 
$\boldsymbol v$ at 
$(\boldsymbol x,t)$. The units of time adopted are 
$1/\omega _{pe}$: the inverse of the electron plasma frequency. When a uniform magnetic field in the 
$z$ direction is present with electron cyclotron frequency 
$\varOmega$ and the background perpendicular velocity distribution is Maxwellian, then the transverse perpendicular velocity dependence can be expressed as a sum over cyclotron harmonics (Hutchinson Reference Hutchinson2018b). The non-adiabatic parallel distribution function perturbation is then
\begin{equation} \tilde f(z,y,v,t) = \exp({{\rm i}(k_\perp y-\omega t)}) \sum_{m={-}\infty}^\infty \tilde f_m(z,v)= \exp({{\rm i}(k_\perp y-\omega t)}) \sum_{m={-}\infty}^\infty b_m \varPhi_m, \end{equation}with
\begin{equation} b_m={\rm i}\left[\omega_m \frac{\partial f_{\parallel0}}{\partial W_\parallel} +m\varOmega \frac{f_{\parallel0}}{T_\perp}\right] q_e{\rm e}^{-\zeta_t^2}{\rm I}_m(\zeta_t^2),\quad \varPhi_m=\int_{-\infty}^t \hat\phi(z(\tau)){\rm e}^{-{\rm i}\omega_m(\tau-t)}\,{\rm d}\tau. \end{equation}
Here 
$\zeta _t^2=k^2T_\perp /\varOmega ^2m_e$, where 
$T_\perp$ is the perpendicular temperature, 
${\rm I}_m$ is the modified Bessel function and 
$\omega _m=m\varOmega +\omega$. The unperturbed equilibrium parallel distribution function depends only on parallel energy 
$W_\parallel$ (not 
$z$ directly) and is written 
$f_{\parallel 0}$, but for the perturbed parallel distributions we omit the 
$\parallel$ subscript for brevity, and from now on omit the 
$y,t$ dependencies as implicitly 
$\exp ({{\rm i}(k_\perp y-\omega t)})$ (so in 
$\varPhi _m$, the upper limit is 
$t=0$). The prior integral 
$\varPhi _m$ is a function of parallel position 
$z$ and velocity 
$v$. The weight 
$b_m$ is independent of 
$z$ but depends on 
$W_\parallel$ through the 
$f_{\parallel 0}$ distribution. We can regard each harmonic 
$m$ as giving a perturbed density contribution 
$\tilde n_m(z)=\int \tilde f_m\, {\rm d}v$. When 
$\hat \phi$ is a sum over modes 
$|u\rangle$,
\begin{equation} \tilde n_m=\tilde{V}_{m}|\hat\phi\rangle=\tilde{V}_{m}\sum_u a_u|u\rangle=\int \sum_u a_u \tilde f_{um} \,{\rm d}v=\sum_u a_u \tilde n_{um}, \end{equation}
where 
$\tilde f_{um}$ denotes 
$\tilde f_m$ with 
$|\hat \phi \rangle =|u\rangle$ substituted in (3.2), and similarly 
$\tilde n_{um}=\int \tilde f_{um}\,{\rm d}v$. Then 
$\tilde V |\hat \phi \rangle =\sum _m\tilde V_m|\hat \phi \rangle =\sum _{u,m}a_u\tilde n_{um}$.
Solving analytically for 
$\varPhi _m$ and 
$n_m$ in the non-uniform equilibrium of an electron hole seems too difficult. The approach taken here is to perform the required integrations numerically. Evaluation of 
$\tilde n_{um}$ is performed using the same code for each 
$m$, but using the different 
$\omega _m$ in (3.3a,b). The inner products we need are 
$\langle s |\tilde V|u\rangle =\int _{-\infty }^\infty s^*(z)\tilde n_{u}(z)\,{\rm d}z$.
3.2 The external continuum wave contribution
In the region far outside the hole, 
$|z/4|\gg 1$ where 
$T=\tanh (z/4)\to \pm 1$ and 
$S={\,{\rm sech}}(z/4)\to 0$ in (2.2), the normalized continuum modes (taking them to be antisymmetrically outward-propagating) are
\begin{align} |p\rangle=A{\rm e}^{{\rm i}\sigma_zpz/4}=\sigma_z\frac{({-}15p^4+225p^2-120) +{\rm i}p (p^{4}-85p^{2}+274)}{[8{\rm \pi}(p^2+1^2)(p^2+2^2)(p^2+3^2)(p^2+4^2)(p^2+5^2)]^{1/2}}{\rm e}^{{\rm i}\sigma_zpz/4}, \end{align}
where 
$\sigma _z={\rm sign}(z)$. Thus they are purely sinusoidal waves. For large enough 
$|z|$ the influence of the local hole potential becomes negligible, and such waves should there be identified with the normal modes of the uniform background plasma. The applicable normal mode for the present electrostatic approximation, in the (usually well-justified) cold electrostatic limit, ignoring ion response, has dispersion relation (including the upper hybrid waves)
\begin{equation} k_\parallel^2/k_\perp^2=\frac{\omega^2(\varOmega^2+\omega_{pe}^2-\omega^2)} {(\varOmega^2-\omega^2)(\omega_{pe}^2-\omega^2)}. \end{equation}
(In our normalized units 
$\omega _{pe}=1$.) Assuming that 
$\omega$ and 
$k_\perp$ are prescribed, there is only one 
$|k_\parallel |$ that satisfies this dispersion relation; and corresponding to it, the continuum eigenmode of 
$V_a$ has 
$k_\parallel =\sigma _zp/4$. The mode number 
$p$ is taken positive, but 
$k_\parallel$ is signed. In this subsection we analyse just this single mode. The approach is mathematically justified in the following subsection.
For a single continuum mode, one can immediately calculate the value of 
$\varPhi _m(z)$ for external positions and inward orbit velocity (e.g. negative 
$v$ on the positive-
$z$ side) using 
$z'=z(\tau )$ and 
$\tau =-(z-z')/v$, as
\begin{align} \varPhi_{m}^{{\rm wave}}(z) = \int_{\sigma_z\infty}^zA\exp({{\rm i}[\sigma_zpz'/4+\omega_m (z-z')/v]})\,{\rm d}z'/v =\frac{A{\rm e}^{{\rm i}\sigma_zpz/4} }{{\rm i}(\sigma_zpv/4-\omega_m)}=\frac{A{\rm e}^{{\rm i}k_\parallel z} }{{\rm i}(k_\parallel v-\omega_m)}, \end{align}
where dropping the infinity limit is justified by positive imaginary part of 
$\omega$. This 
$\varPhi _{m}^{{\rm wave}}$ for the external region applies for all 
$z$ down to where the eigenmode begins to deviate significantly, because of non-zero hole potential, from the external wave; obviously that 
$z$ is of the order of a few times 4.
The non-adiabatic distribution perturbation for outward (positive 
$v$ at positive 
$z$) orbit velocity, by contrast, is strongly affected by the rapid variation of potential across the hole at 
$z\sim 0$ whose effect is carried into the external region by the particle orbits. However, for large enough 
$|z|$ the effects of the hole and earlier parts of the orbit become negligible because of dephasing between oscillatory contributions from different velocities. The dephasing effect attenuates the influence on density in a distance of several times 
$z_l\sim 1/\omega _m$, which is finite but (for 
$m=0$ at least) typically exceeds the hole extent itself (
${\sim }4$) because 
$\omega$ is small. Thus the very distant (
$|z|\gg z_l$) 
$\tilde n$ perturbations for inward- and outward-going velocities are given approximately by integrating 
${\rm d}v$ the same 
$\varPhi _m^{{\rm wave}}$ expression for 
$z\gg z_l$, but with 
$v$ of opposite sign.
The total wave density perturbation can then be considered to be a constant 
$\tilde V_m^{{\rm wave}}$ times 
$|p\rangle$, where
\begin{equation} \tilde V_m^{{\rm wave}}= \int_{-\infty}^\infty \frac{ b_m(v) }{{\rm i}(k_\parallel v-\omega_m)} \,{\rm d}v. \end{equation}
If 
$f_{\parallel 0}$ is an unshifted Maxwellian, and only 
$m=0$ is included, the total wave operator 
$\tilde V_w\equiv \sum _m\tilde V_m^{{\rm wave}}$ is proportional to the plasma dispersion function 
$Z$, and in the small 
$k_\parallel /\omega$ limit becomes 
$\tilde V_w=1+(k_\parallel /\omega )^2$. However, that approximation effectively implements the limit 
$\varOmega \gg \omega _{pe}$, and gives a dispersion relation 
$k_\parallel ^2/k_\perp ^2 = \omega ^2/(\omega _{pe}^2-\omega ^2)$, rather than the full cold plasma expression for finite 
$\varOmega /\omega$: (3.6). The full expression arises when the 
$|m|=1$ terms in the harmonic sum for the kinetic electrostatic dispersion relation (see e.g. Swanson Reference Swanson1989, § 4.4) are also included, to lowest order in 
$\zeta _t^2$. The resulting analytic form is
\begin{equation} \tilde V_w= 1 + \left(\frac{k_\parallel}{\omega}\right)^2 + k_\perp^2 \frac{T_\perp{/}T_\parallel}{\omega^2-\varOmega^2}. \end{equation} The crucial point is that 
$(\tilde {V}-\tilde {V}_{w})|q\rangle$ is localized, tending to zero in the region beyond 
$z_l$, which means that overlap integrals of the form 
$\langle p |\tilde {V}-\tilde {V}_{w}|q\rangle$ exist finite over an infinite domain. An important secondary feature is that, for external positions 
$|z|\ge z_d$ (where the effective hole edge 
$z_d$ is great enough that 
$\phi _0(z_d)=0$), the inward velocity part of 
$\tilde V_m^{{\rm wave}}$, consisting of
\begin{equation} \tilde V_m^{{\rm in}}= \int_{0}^\infty \frac{ b_m(-\sigma_x|v|) }{{\rm i}(-|k_\parallel v|-\omega_m)}\sigma_x \,{\rm d}|v|, \end{equation}
is exactly equal to the actual non-adiabatic density perturbation that accounts for the hole's presence and the full eigenmode structure. So the cancellation of the part of 
$\tilde V-\tilde V_w$ for inward orbits only is exact 
$(\tilde V^{{\rm in}}-\tilde V_m^{{\rm in}})|q\rangle =0$. Therefore the non-zero contribution to external region 
$z$ integrals of 
$(\tilde V-\tilde V_w)|q\rangle$ arises only from outward orbits 
$(\tilde V^{{\rm out}}-\tilde V_m^{{\rm out}})|q\rangle \neq 0$. The necessary integral of outward orbits, however, must be carried out to an upper limit for which 
$|z|\gg z_l\gg z_d$. We consider explicitly only parallel distributions 
$f_{\parallel 0}$ that are symmetric in 
$v$. In that case 
$b_m$ is symmetric, and the overlap integrals can be calculated for a single sign of 
$v$ and then doubled to give the total.
3.3 Reducing the continuum to give the dispersion matrix
Now we discuss mathematically how the previous considerations allow us to reduce the continuum contribution to effectively a single mode. Using 
$s,u\to q,p$ etc. to observe our notation for continuum modes, and supposing them to be normalized (
$\langle q |p\rangle =\delta _{qp}$), we write the continuum part of (2.10) explicitly as an integral 
$a(p)\,{\rm d}p$ over an amplitude distribution function 
$a(p)$ rather than a sum. Proceeding with no assumption about the size of cross-coupling of secondary modes, the eigenmode equation inner product with mode 
$\langle s |$ gives the re-expressed (2.10) as
\begin{equation} 0=(\lambda_s-\lambda_\perp)\langle s|s\rangle a_s+\sum_j\langle s|\tilde{V}|j\rangle a_j +\int\langle s|\tilde{V}|p\rangle a(p)\,{\rm d}p. \end{equation}
We apply this equation for the three modes 
$s=4,2,q$. First for the continuum mode (
$\langle s |=\langle q |$) with the adiabatic terms moved to the left-hand side:
\begin{equation} (-\lambda(q)+\lambda_\perp)a(q)=\sum_j\langle q|\tilde{V}|j\rangle a_j +\int\langle q|\tilde V|p\rangle a(p)\,{\rm d}p. \end{equation}
We write the continuum integral using 
$\langle q |\tilde V_w|p\rangle = \tilde V_w \delta _{qp}$ as
\begin{align} \int \langle q|\tilde{V}|p\rangle a(p)\,{\rm d}p=\int\langle q|\tilde{V}_{w}+(\tilde{V}-\tilde{V}_{w})|p\rangle a(p)\,{\rm d}p =\tilde{V}_{w}a(q) +\int\langle q|(\tilde{V}-\tilde{V}_{w})|p\rangle a(p)\,{\rm d}p. \end{align}
The final term can be approximated by observing that, by construction, 
$\tilde V -\tilde V_w$ is significant only in the inner 
$z$ region. As can be seen in figure 1, the form of the continuum modes in the inner region is almost independent of 
$p$. (Actually for small 
$p$, which is our interest here, the differences are even smaller than that figure shows.) Therefore, to that degree of approximation, we can replace 
$|p\rangle$ with 
$|q\rangle$ in the final term, giving 
$\int \langle q |(\tilde {V}-\tilde {V}_{w})|p\rangle a (p)\,{\rm d}p\simeq \langle q |\tilde {V}-\tilde {V}_{w}|q\rangle \int a(p)\,{\rm d}p$, and obtain the equation
\begin{equation} (-\lambda(q)+\lambda_\perp{-}\tilde V_w)a(q)=\sum_j\langle q|\tilde{V}|j\rangle a_j +\langle q|\tilde V-\tilde V_w|q\rangle\int a(p)\,{\rm d}p. \end{equation}
Since (by the approximate invariance of the continuum modes in the inner region) the right-hand side is a weak function of 
$q$, this equation implies that 
$a(q)$ is a resonant function of 
$q$ centred on the 
$q$ value for which its coefficient on the left-hand side is approximately zero. We can write the coefficient of 
$a(q)$ using (2.3) 
$-\lambda (q)=k_\parallel ^2+1$ and (3.9) as
\begin{align} k_\parallel^2+k_\perp^2+1-\tilde V_w\simeq k_\perp^2\left(1-\frac{T_\perp{/}T_\parallel}{\omega^2-\varOmega^2}\right) +k_\parallel^2\left(1-\frac{1}{\omega^2}\right) = \frac{1}{4^2}\left(\frac{1}{\omega^2}-1\right)(q_0^2-q^2), \end{align}where
\begin{equation} \left. q_0=4k_\perp\sqrt{1+\frac{T_\perp{/}T_\parallel}{\varOmega^2-\omega^2}} \right/\sqrt{\frac{1}{\omega^2}-1}. \end{equation}
The coefficient 
$(-\lambda (q)+\lambda _\perp -V_w)$ is zero when 
$q^2=q_0^2$, which is the dispersion relation of the wave in a uniform plasma. It is equal to the cold plasma expression (3.6) when 
$T_\perp /T_\parallel =1$.
We integrate (3.14) 
${\rm d}q/(\lambda _\perp -\lambda (q)-V_w)$, recognizing again the approximate independence of 
$q$ of the right-hand side to find
\begin{equation} \int a(q) \,{\rm d}q =\int \frac{{\rm d}q}{\lambda_\perp{-}\lambda(q)-V_w} \left(\sum_j\langle q|\tilde{V}|j\rangle a_j +\langle q|\tilde V-\tilde V_w|q\rangle\int a(p)\,{\rm d}p \right). \end{equation} In view of the resonant form of the expression for 
$a(q)$, we can regard the integral over this resonance 
$\int a(q) \,{\rm d}q$ as quantifying the total continuum perturbation. The integral encounters the two poles of the integrand at 
$q=\pm q_0$. Near them the real part of 
$(\lambda _\perp -\lambda (q)-V_w)$ becomes small. Its imaginary part comes from the small, necessarily positive, imaginary part of 
$\omega =\omega _r+{\rm i}\omega _i$. It can then quickly be shown that 
$q_0$ has a small positive imaginary part: 
$q_0=q_{0r}+{\rm i}\epsilon$.
The infinite integral along the real 
$q$ axis can be closed by returning in the upper part of the complex plane (
$\mathrm {Im}(q)$ positive) where the eigenmode tends to zero. The resonant integral is then just 
$2{\rm \pi} {\rm i}$ times the residue at the positive 
$q_0$ pole, which is the mathematical justification for our physical assumption of outwardly propagating waves. Writing it 
$\int ({{\rm d}q}/{\lambda _\perp -\lambda (q)-V_w})=1/K$, we find
\begin{equation} K\simeq\frac{(1/\omega^2-1)q_0}{16{\rm \pi} {\rm i}} = \frac{k_\perp}{4{\rm \pi} {\rm i}}\sqrt{\frac{1}{\omega^2}-1} \sqrt{1+\frac{T_\perp{/}T_\parallel}{\Omega^2-\omega^2}}. \end{equation}
Substituting elsewhere the value 
$q=q_0$ at the integrand's pole, and introducing the shorthand notation 
$\int a(p) \,{\rm d}p= a_q$ (omitting the subscript 0 on 
$q$), (3.17) becomes
\begin{equation} (K-\langle q_0|\tilde V-\tilde V_w|q_0\rangle)a_q = \sum_j\langle q_0|\tilde{V}|j\rangle a_j. \end{equation} Treatment of the discrete modes uses again the approximation that over the resonance 
$\langle j |\tilde V|p\rangle$ can be regarded as independent of 
$p$; then for 
$l=4,2$:
\begin{align} (\lambda_\perp{-}\lambda_l)a_l=\sum_j\langle l|\tilde{V}|j\rangle a_j +\int\langle l|\tilde{V}|p\rangle a(p)\,{\rm d}p =\sum_j\langle l|\tilde{V}|j\rangle a_j +\langle l|\tilde{V}|q_0\rangle\int a(p)\,{\rm d}p. \end{align}
We regard the amplitudes of the three modes 
$4,2,q_0$ as composing a column 3-vector whose transpose is
\begin{equation} \boldsymbol{\mathsf{a}}^T=(a_4,a_2,a_q)=(a_4,a_2,\int a(p)\,{\rm d}p). \end{equation}
The three relations in (3.19) and (3.20) can be considered a matrix equation 
$\boldsymbol{\mathsf{M}}\boldsymbol{\mathsf{a}}=0$, where
\begin{equation}
\boldsymbol{\mathsf{M}}=\left[ \begin{array}{@{}ccc@{}}
\lambda_4-\lambda_\perp{+}\langle4|\tilde V|4\rangle &
\langle4|\tilde V|2\rangle & \langle4|\tilde V|q_0\rangle\\
\langle2|\tilde V|4\rangle &
\lambda_2-\lambda_\perp{+}\langle2|\tilde V|2\rangle &
\langle2|\tilde V|q_0\rangle\\ \langle q_0|\tilde
V|4\rangle & \langle q_0|\tilde V|2\rangle & -K+\langle
q_0|\tilde V-\tilde V_w|q_0\rangle \end{array}\right].
\end{equation}
The complex determinant of 
${\mathsf{M}}$ must be zero for a non-trivial solution. To connect more directly with the shiftmode calculation, which simply zeroes the top-left coefficient 
${\mathsf{M}}_{11}$, and to avoid large values arising from 
${\mathsf{M}}_{33}$, the scaled quantity (denoted 
$D$) we actually zero is the determinant of 
${\mathsf{M}}$ divided by the co-factor of 
${\mathsf{M}}_{11}$. If 
$\omega$ is iterated until 
$D=0$, the 
$\omega$ value found will be the corresponding mode frequency, and the mode structure will be given by the solution of 
$\boldsymbol{\mathsf{M}}\boldsymbol{\mathsf{a}}=0$.
Our reduction of the resonant continuum mode uses just the 
$m=0,\pm 1$ cyclotron harmonics to determine 
$q_{0}.$ That is justified by supposing that the finite Larmor radius parameter 
$\zeta _t=k_\perp \sqrt {T_\perp /m_e}/\varOmega$ is small, and recognizing 
${\rm I}_m(\zeta _t^2)\propto \zeta _t^{2m}$. If instead 
$\zeta _t$ is not small (because 
$\varOmega \not \gg k_\perp v_{t\perp }$), the dependence 
${\rm e}^{-\zeta _t^2}$ predominates in (3.2), and harmonics up to 
$|m|\sim 3\zeta _t$ approximate a continuous integral over the perpendicular Maxwellian, with the relevant range of 
$\omega _m$ approximately 
$\omega \pm 3k_\perp v_{t\perp }$. The resultant frequency spread exceeds 
${\sim }\omega$ for the whistler mode (for which 
$\omega < \varOmega$) implying that high-harmonic (i.e. perpendicular Landau) damping is strong. The continuum mode contribution itself is then suppressed, and it is reasonable to ignore coupling to the continuum modes, reducing 
$\boldsymbol{\mathsf{M}}$ to its upper-left 
$2\times 2$ submatrix.
4 Evaluation of matrix elements
4.1 Internal numerical evaluation of inner products
The evaluation of the overlap integrals (forces) that appear in 
$\boldsymbol{\mathsf{M}}$ for the inner hole region is carried out numerically using methods that have been documented in detail previously (Hutchinson Reference Hutchinson2018b) for mode 
$|4\rangle$. In summary the process consists, for each relevant orbit energy 
$W$, of numerically integrating to obtain the relationship between 
$z$ and the prior time 
$\tau$ for the unperturbed orbit, and simultaneously accumulating the integral 
$\varPhi _m(z)$ for each mode, using a discrete (but non-uniform) 
$z$ mesh. Trapped orbits 
$W<0$ require a sum over all prior bounces in the potential well, which is represented by a multiplying bounce-resonant factor. Passing orbits use a single transit across the domain 
$-z_d< z< z_d$, and for the discrete modes there is no external contribution. The continuum mode at the incoming boundary (
$z_{{\rm in}}=-(v/|v|)z_d$), unlike the discrete modes, has a non-zero value, which is provided by the wave expression 
$\varPhi _m(z_{{\rm in}})=\varPhi _m^{{\rm wave}}$, (3.7). Inside the prior time integration loop, the overlap integrals 
$\int s^*(z)\tilde f_m(z)\,{\rm d}z$ are simultaneously accumulated. Afterwards they are integrated 
${\rm d}v$ over the relevant range of parallel energy 
$W$, and summed over relevant harmonics 
$m$ to give the hole-region contributions to 
$\langle s |\tilde V|u\rangle$. Except when 
$s$ is the continuum mode (the bottom row of 
$\boldsymbol{\mathsf{M}}$), these internal values provide the full evaluation of the overlap integrals. For 
$s=q_0$, however, extra contributions arise from the external region, which we now describe.
4.2 External analytic integration
In the external region 
$|z|>z_d$, the prior integral 
$\varPhi$ giving 
$\tilde f$ for discrete modes 
$|j\rangle$ is non-zero only for outward-moving orbits. We focus for definiteness on 
$z>z_d$ and positive 
$v$. For inward-moving orbits, by contrast, 
$\tilde f$ is zero externally for the operations 
$\tilde V|j\rangle$ and 
$(\tilde V -\tilde V_w)|q_0\rangle$. Consequently, the external contribution to the forces 
$\langle q _0|\tilde V |j\rangle$ and 
$\langle q _0|\tilde V -\tilde V_m|q_0\rangle$ arises from the external integration 
$\int _{z_d}^\infty q_0^*(z) \tilde n \,{\rm d}z$ only for outward orbits, indicated by superscript ‘out’ on 
$\tilde V$.
To assist with understanding, figure 2 shows a case illustrating the relevant density perturbations 
$\tilde n_q=\tilde V^{{\rm out}}|q\rangle$, 
$\tilde n_w=\tilde V_w^{{\rm out}}|q\rangle$ and 
$\tilde n_4=\tilde V|4\rangle$ arising from positive velocity orbits. The upper panel shows the relevant curves for the continuum mode in the inner and outer regions. The densities 
$\tilde n_q$ and 
$\tilde n_w$ are very different in the inner region 
$|z|\lesssim z_d$ and well outside it but they converge to each other in the wave region 
$|z|\gg z_l$ (
$z_l\sim 20$ for this relatively high-frequency illustration). Also shown is the curve of 
$\tilde V_w|q\rangle /2$ which is the average of the inward and outward densities. It has a shape similar to 
$\tilde n_w$ but is somewhat smaller because 
$\tilde V^{{\rm in}}< \tilde V^{{\rm out}}$. The relevant contribution comes from the difference between 
$\tilde n_q$ and 
$\tilde n_w$.
Figure 2. Illustrating the process of calculating the inner products involving 
$|q_0\rangle$ and 
$|4\rangle$. Passing density contributions from positive, outward, velocity orbits integrated over all relevant energies. The square symbol locates the edge of the inner hole region, chosen here as 
$z_d=15$. The scaled 
$\varPhi$ shown is for the last included energy 
$W=6$.
The lower panel shows 
$\tilde n_4$ which is substantial in the inner region and converges to zero for 
$|z|\gg z_l$, and one can see residual oscillations caused by discrete contributions at low velocity approximating the 
${\rm d}v$ integral, which die out at large 
$z$. In the upper panel there are also some oscillations but they are barely visible. The ‘
$\varPhi$ (scaled)’ curve illustrates (only) the shape of the final contribution to the velocity integral from high velocity, showing how long the wavelength of oscillations becomes there; its contribution to 
$\tilde n$ is small because 
$f_{\parallel 0}$ is negligible at high 
$v$.
Now we explain how the external integrations are performed mostly analytically. In the external region, the velocity is constant; so for 
$|j\rangle$, which has zero perturbed potential there, 
$\varPhi$ is a simple time delay factor multiplied by its value at the join between internal and external regions 
$\varPhi (z_d)$:
\begin{equation} \varPhi_{|j\rangle}(z)=\exp({{\rm i}\omega_m(z-z_d)/v}) \varPhi_{|j\rangle}(z_d). \end{equation}
The corresponding expression for the continuum mode, which has non-zero external potential, may be found by substituting the wave expression (3.7) for 
$|q_0\rangle$ which can be integrated analytically to give an extra term, arriving at
\begin{align} \varPhi_{|q_0\rangle}(z)=\exp({{\rm i}\omega_m(z-z_d)/v}) \varPhi_{|q_0\rangle}(z_d) +\frac{A\exp({{\rm i}k_\parallel z_d})}{{\rm i}(k_\parallel v-\omega_m)}[\exp({{\rm i}k_\parallel(z-z_d)}) -\exp({{\rm i}\omega_m(z-z_d)/v})]. \end{align}
Recalling that the wave operator is simply constant, its external contribution to 
$\varPhi _{|w\rangle }$ for a particular positive velocity is 
${A{\rm e}^{{\rm i}k_\parallel z}}/{{\rm i}(k_\parallel v-\omega _m)}$, which exactly cancels the first term in the square bracket of 
$\varPhi _{|q_0\rangle }(z)$. Such cancellation is essential to produce a finite value for 
$\langle q _0|\tilde V -\tilde V_w|q_0\rangle$. Hence, when forming 
$(\tilde V -\tilde V_w)|q_0\rangle$, the required external prior integral is
\begin{align} \varPhi_{|q_0-w\rangle}(z)\equiv \varPhi_{|q_0\rangle}(z)-\varPhi_{|w\rangle} =\exp({{\rm i}\omega_m(z-z_d)/v}) \varPhi_{|q_0\rangle}(z_d) -\frac{A\exp({{\rm i}k_\parallel z_d})}{{\rm i}(k_\parallel v-\omega_m)} \exp({{\rm i}\omega_m(z-z_d)/v}). \end{align}
To obtain the total external force we can carry out the inner product 
$z$-integration analytically as
\begin{equation} \int_{z_d}^\infty q_0^*(z) \varPhi_u(z) \,{\rm d}z = \frac{A^*\varPhi_u(z_d)v{\rm e}^{-{\rm i}k_\parallel z_d}}{{\rm i}(k_\parallel v-\omega_m)} + \frac{\delta_{q_0u}|A|^2v}{(k_\parallel v-\omega_m)^2}, \end{equation}
where 
$\varPhi _u$ refers to the ‘ket’ mode (
$j$ or 
$q_0-w$) and the 
$|A|^2$ term is present only if we are constructing 
$\langle q _0|\tilde V -\tilde V_w)|q_0\rangle$, as indicated by 
$\delta _{q_0u}$. This force quantity is multiplied by the weighting factor 
$b_m$ (3.3a,b) and integrated (numerically) over parallel velocity so as to produce the total inner product. For asymmetric 
$f_{\parallel 0}$ the process would need to be carried out also for negative velocity and 
$z$, but since we take 
$f_{\parallel 0}$ to be symmetric the integration is carried out only for positive 
$v$ and 
$z$; the result is then doubled to account for force exerted at negative 
$z$. The sum over relevant cyclotron harmonics 
$m$ is performed last.
In verification of the fairly complex coding we have compared results for mode 
$|4\rangle$ with prior calculations, confirmed certain analytic self-adjoint properties of the different modes and debugged the 
$m=0$ results by benchmark comparisons between two independent implementations of the calculation (in Fortran and Python).
5 Results
Figure 3 gives a comprehensive overview of the the existence of instability as a function of magnetic field strength, in appropriately scaled units; frequencies (figure 3a) are generally proportional to 
$\sqrt {\psi }$ (except at high magnetic field beyond the plotted range), and the scaled figure changes only a little for different values of 
$\psi$. There are broadly three field-strength regimes, as has been documented in prior publications. At low magnetic field 
$\varOmega /\sqrt {\psi }\lesssim 0.35$, a purely growing instability exists: 
$\omega _r=0$, 
$\omega _i>0$. At intermediate field 
$0.35\lesssim \varOmega /\sqrt {\psi }\lesssim 0.65$, an oscillating instability 
$\omega _r>0$ exists with growth rate only of the order of a factor of two smaller than the low-field regime. At higher field 
$0.65\lesssim \varOmega /\sqrt {\psi }$, growth rates 
$\omega _i$ are either zero, indicating no instability was found, or extremely small but positive, which occurs increasingly at higher 
$\varOmega /\sqrt {\psi }$ (and lower 
$k_\perp$); the unstable high-field cases have real oscillation frequencies comparable to those in the intermediate regime. We plot also, in the lower panel of figure 3(a), the difference 
$\delta \omega$ between the frequencies found by the multimode and shiftmode calculations. These differences are generally small and the different 
$\omega$ scale should be noted. Their imaginary part 
$\delta \omega _i$ is always positive in the low-field regime, almost always positive in the intermediate regime and almost always negative (and much smaller) in the high-field regime. The real part 
$\delta \omega _r$ has some positive differences in the intermediate regime, especially its upper end, but elsewhere is very small.
Figure 3. (a) Frequency 
$\omega$ and frequency difference between multimode and shiftmode calculations 
$\delta \omega$ and (b) additional mode amplitudes 
$a_2/a_4$ and 
$a_q/a_4$, all as a function of 
$\varOmega$, but for four different values of 
$k_\perp$.
The additional mode amplitudes (figure 3b) accompanying these calculations show that the discrete mode 2 real amplitude is substantial and generally negative in the two lower-field regimes, but slightly positive in the high-field regime. Its imaginary amplitude is substantial only in the upper part of the intermediate regime. The continuum mode amplitude is effectively zero in the purely growing regime, but substantially negative imaginary in the intermediate regime. It is mostly real, negative and somewhat smaller in the high-field regime.
The overall picture is that there are only rather small differences between the multimode and shiftmode eigenfrequencies, and that almost all results show the multimode to be somewhat more unstable in the two lower-field regimes. This summary is in reasonable agreement with prior expectations. The additional multimode shape flexibility slightly enhances instability growth rates, but overall the shiftmode gives rather accurate eigenfrequencies.
To help explain the mechanisms underlying the three regimes, figure 4 shows contours in the 
$\omega$ plane of the residual of the force balance parameter whose roots are found in the prior figures. Figure 4(a) shows the high-field regime, plotting contours of the real and imaginary parts of the pure shiftmode force balance 
${\mathsf{M}}_{11}$. The eigenfrequency is where the two zero contours (blue and green solid lines) intersect, at very small 
$\omega _i$. In addition, the zero contours of 
$D$, the multimode equation, are plotted as long-dashed lines. Actually the real 
$D=0$ contour is invisible, but lies just below the (corresponding) imaginary 
${\mathsf{M}}_{11}=0$, where 
$\omega _i$ is small. The two calculations agree on the eigenfrequency quite closely; more detail is given of this regime later.
Figure 4. Contours of force balance quantities which should be zero for the eigenfrequency. (a) High-magnetic-field regime showing shiftmode contours and multimode zero contours (long-dashed curves). (b) Low-field regime showing multimode 
$D$ contours and shiftmode zero contours (long-dashed curves), but also the Newton steps to convergence.
Figure 4(b), by contrast, shows the low-field regime in which the instability is purely growing. Contours of 
$D$ are shown, plus the zero shiftmode contour of 
${\mathsf{M}}_{11}$; the zero imaginary contours coincide with the vertical axis. The Newton iterations, which find this intersection precisely, are indicated with iteration numbers at the corresponding frequencies. The multimode growth rate slightly exceeds that of the shiftmode. The mechanisms governing the instability are the same as those identified in shiftmode analysis (Hutchinson Reference Hutchinson2018a, Reference Hutchinson2019b).
The intermediate-field regime is illustrated in figure 5. In figure 5(a) we show the contours, and observe this to be a case where there is a visible difference between the locations of the zero intersections (the eigenfrequencies) in the vicinity of 
$\omega /\sqrt {\psi }=0.11+0.01{\rm i}$, for multimode and shiftmode. This difference arises mostly from the real part of 
$D$. In figure 5(b) are shown plots of the corresponding multimode potential perturbation as a function of position 
$z$. In the upper panel one sees that in addition to mode 4 contribution, which far exceeds the vertical axis length, there is a substantial (up to 0.08) real contribution from mode 2 (
$a_2/a_4=-0.21-0.025{\rm i}$). The resultant total (real) mode shape is shown in the lower panel by the solid line, with the mode 4 contribution alone shown dotted. We observe that the mode 2 contribution increases the total perturbation for 
$|z|\lesssim 0.25$ and decreases it for 
$|z|\gtrsim 0.25$. The multimode distortion tends to enhance the influence of deeply trapped particles (concentrated near 
$z=0$) and decrease that of marginally trapped particles, which spend most of their time at large 
$|z|$. This effect qualitatively explains the greater growth rate of the multimode instability because, as has been noted before (Hutchinson Reference Hutchinson2019b), the deeply trapped particles drive the instability in this regime, while the marginally trapped tend to stabilize it. In further support of this interpretation, figure 6 compares the mode shape observed in prior PIC simulations (Hutchinson Reference Hutchinson2019b) with the total mode shape calculated by the present analysis. The parameters are very similar, 
$\psi =0.16$, 
$\varOmega /\sqrt {\psi }=0.68$, 
$k_\perp /\sqrt {\psi }=0.6$, and are at the upper end of the intermediate-field regime. The coupled amplitude of 
$|2\rangle$ for the converged eigenfrequency (
$\omega =0.12+0.0022{\rm i}$) is very substantial: 
$a_2/a_4=-0.51$. This implies a multimode shape considerably narrowed from the raw 
$|4\rangle$ shape, with some overshoot. The observed PIC simulation mode shape is similarly narrowed, which is highly suggestive. However, the PIC mode is slightly narrower and does not show overshoot, which we take as an indication that for such an extreme case even the multimode treatment is not quite sufficient to represent the most unstable mode, perhaps because the expansion in adiabatic eigenmodes is no longer adequate. We remark that the real parts of the found frequencies agree very well, but the PIC growth rate was observed to be 
${\sim }0.004$, a factor of approximately 2 larger than the multimode calculation. No analytic pure shiftmode instability was found for these parameters.
Figure 5. (a) Intermediate field dispersion contours. (b) Contributions to the multimode potential perturbation.
Figure 6. Scaled (total) mode shapes found from multimode analysis compared with shape observed in a PIC simulation having similar parameters: 
$\psi =0.16$, 
$\varOmega /\sqrt {\psi }=0.68$, 
$k_\perp /\sqrt {\psi }=0.6$.
At very high magnetic field 
$\varOmega \gtrsim 5$, the approximation of one-dimensional motion can be used, and dependence on 
$B$ disappears from the calculations. It has previously been shown that shiftmode analysis indicates a very slowly growing overstability that agrees approximately with simulations (Hutchinson Reference Hutchinson2019a). Bounce resonance provides a stabilizing contribution to it because the mode has negative energy. An example comparison of contours calculated with multimode and shiftmode analysis is given in figure 7. Multimode analysis finds an unstable eigenfrequency at 
$\omega =0.0285+0.0002{\rm i}$, whose growth rate is a factor of nearly 3 lower than that of the shiftmode. The differences are essentially entirely caused by coupling to a small, predominantly real, amplitude of the continuum, 
$a_q/a_4=-0.014-0.0018{\rm i}$. (The negligible influence of 
$|2\rangle$, for which 
$a_2/a_4=0.002-0.0001{\rm i}$, has been verified, for example, by temporarily removing 
$|q\rangle$ but not 
$|2\rangle$ from the analysis, and finding agreement with shiftmode.) The shiftmode zero contours are the long-dashed lines. The real-part zero contour of 
$\omega$ is essentially unchanged by inclusion of the continuum mode, but the imaginary zero contour is suppressed to lower 
$\omega _i$. Cases with smaller 
$\psi$ see somewhat less multimode suppression, but they have a very small growth rate anyway, since 
$\omega _i$ scales approximately as 
$\psi ^{3/2}$. In no case has the high-
$B$ instability been demonstrated to be completely stabilized in this multimode infinite-domain analysis, but for 
$\psi \lesssim 0.2$ the predicted growth time is far longer than probable hole lifetimes.
Figure 7. Reduction of the high-field instability growth rate by the influence of the continuum mode.
Prior high-
$B$ simulations observed somewhat higher growth rate than predicted by shiftmode analysis. The multimode analysis giving lower growth rate appears to rule out explanation of this observation by mode distortion, and to favour the cause being suppression in the simulations of the bounce resonance stabilization by reduced 
${\rm d}f/{\rm d}W$ for shallow trapped orbits. However, the simulations are for finite, not infinite, parallel domain length. We can definitely conclude from the present infinite-domain analysis that coupling to the continuum mode is a significant effect, which is in line with previous interpretations; but we cannot directly apply our analysis to simulations of limited domain length.
6 Discussion
The analysis here uses a specific potential shape 
$\phi _0\propto {\,{\rm sech}}^4(z/4)$. This is the shape most widely advocated as ‘natural’ for electron holes. It is by no means unique, but it is part of the family 
${\,{\rm sech}}^l(z/l)$ that satisfies the Debye shielding requirement that the potential decays 
$\propto \exp (-z/\lambda _{De})$ at large 
$|z|$. Members of this family have the number of discrete adiabatic eigenmodes equal to 
$l+1$ (see Appendix A). Higher 
$l$ corresponds to a broader profile at its peak and would call for more than the two discrete antisymmetric modes we have analysed here. That possibility also exists for broader profiles of different mathematical form, not having the convenience of closed analytic expressions for their eigenmodes. We believe that the current choice is representative, and that the same qualitative trends would be observed for other profiles.
We also here take the domain boundary to be at infinity. This is the natural idealization for an isolated hole. However, simulations always deal with finite (usually periodic) domains. They would require a different treatment of the continuum modes. External waves would be restricted to a discrete set of wavenumbers that satisfies the boundary conditions, and the continuum become discrete. A perhaps more important difference is that in a finite domain there will be inward-propagating waves (perhaps as components of standing waves) as well as the outward ones of the present treatment. As a result, the length of the parallel domain will determine whether certain waves are or are not coupled resonantly to the perturbed electron hole. The result could perhaps be stabilizing or destabilizing, depending on domain size. Accommodating incoming waves would require a major modification of the analysis, which is beyond our present scope. The infinite domain analysed here properly represents truly isolated electron holes. Exactly periodic analysis would not correctly represent electron holes in nature, even if they are part of an irregularly spaced train of holes.
Although our focus here has been on the non-zero 
$k_\perp$ transverse instability, some similar adjustments to the stability might arise in purely one-dimensional oscillatory phenomena. For example, some regimes of slow electron holes, whose speeds are close to the ion velocity distribution, experience one-dimensional oscillatory instabilities (Zhou & Hutchinson Reference Zhou and Hutchinson2017; Hutchinson Reference Hutchinson2021), and their growth rates might be modified in multimode analysis. However, it seems likely that the multimode corrections would be relatively small, as observed in our present work. Ion response is negligible for holes moving faster than a few times the ion sound speed. We have also treated here only symmetric electron distributions, which limits the quantitative reliability to holes that are not moving at a large fraction of the electron thermal speed. The very considerable additional complexity of including ions and asymmetry hardly seems justified within the present context.
In summary, it has been shown how to perform multimode analysis of electron hole transverse instability, identifying the key effects as being (1) modification of the effective width of the eigenstructure, corresponding to an additional discrete eigenmode of the adiabatic Poisson operator, and (2) coupling to external waves on the whistler branch, corresponding to a narrow band of the adiabatic operator's continuum. The width effect slightly increases the growth rate at low and intermediate magnetic field, and permits relatively fast-growing overstability at magnetic fields up to 
$\sim$20 % above the prior shiftmode maximum. The total mode shape is similar to that observed in PIC simulations. The external wave coupling decreases the growth rate at high magnetic field. Despite these adjustments, the prior single-shiftmode analysis is confirmed as giving results very close, in most cases, to those of the multimode analysis.
Acknowledgements
The work of X.C. was initially supported by NASA grant NNX16AG82G, and later in part by US DOE contract DE-SC0019089. No external data were used. The figures were calculated using code available at https://github.com/ihutch/multimodeEH.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Eigenmode derivation
The adiabatic operator (generalizing (2.1)) for equilibrium 
$\phi _0={\,{\rm sech}}^{n-1}(z/l)=S^{n-1}$ is 
${{\rm d}^2}/{{\rm d}z^2}+[n(n+1)S^2-(n-1)^2]/l^2$. Define the operator for positive 
$n\in \boldsymbol {Z}$: 
$L_n=l^2({{\rm d}^2}/{{\rm d}z^2})+{n(n+1)} S^2$; define also the operators 
$L^+_n=l({{\rm d}}/{{\rm d}z})+n T$, 
$L^-_n=l({{\rm d}}/{{\rm d}z})-n T$, where 
$T=\tanh (z/l)$. Then
\begin{align} \left. \begin{aligned} & L^+_n L^-_n=l^2\frac{{\rm d}^2}{{\rm d}z^2}-n S^2-n^2
T^2=L_{n-1}-n^2,\\ & L^-_n L^+_n=l^2\frac{{\rm d}^2}{{\rm
d}z^2}+n S^2-n^2 T^2=L_n-n^2. \end{aligned} \right\}
\end{align}
Using these properties, we immediately find that
\begin{align} L_n L^-_n=(L^-_n L^+_n+n^2)L^-_n=L^-_n (L^+_n L^-_n)+n^2L^-_n=L^-_n (L_{n-1}-n^2)+n^2 L^-_n=L^-_n L_{n-1}, \end{align}
which shows that 
$L^-_n$ can be considered a raising ladder operator in the sense that 
$L_n=L^-_nL_{n-1}(L^-_n)^{-1}$. As a result, (A2) leads to
\begin{align} L_n L_n ^- L_{n-1}^- \cdots L_1^-&=L^-_n L_{n-1}L_{n-1}^- \cdots L_1^-{=}L^-_n L_{n-1}^- L_{n-2}L_{n-2}^- \cdots L_1^-\nonumber\\ & = \cdots = L_n ^-L_{n-1}^- \cdots L_1^- L_0. \end{align} The eigenfunctions of 
$L_0$ have the form 
$|e_0\rangle =\textrm {e}^{uz/l}$ with eigenvalue 
$u^2$, where 
$u$ can be either real or imaginary. Specializing to our current case, 
$n=l+1=5$ in (A3) we have
\begin{equation} L_5 L_5 ^- L_4^- \cdots L_1^- |e_0\rangle = L_5 ^- L_4^- \cdots L_1^- L_0 |e_0\rangle =u^2 L_5 ^- L_4^- \cdots L_1^- |e_0\rangle. \end{equation}
Therefore, 
$|u\rangle =L_5 ^- L_4^- \cdots L_1^- |e_0\rangle$ is an eigenfunction of 
$L_5$ with eigenvalue 
$u^2$. Since 
$V_a=L_5/l^2-1=L_5/4^2-1$, 
$|u\rangle$ is also an eigenfunction of 
$V_a$ but the corresponding eigenvalue becomes 
$u^2/16-1$. Written out in full,
\begin{align} |u\rangle&= L_5^- L_4^- L_3^- L_2^-L_1^-{\rm e}^{uz/l} \nonumber\\ &=\left(l\frac{{\rm d}}{{\rm d}z}-5T\right)\left(l\frac{{\rm d}}{{\rm d}z}-4T\right)\left(l\frac{{\rm d}}{{\rm d}z}-3T\right)\left(l\frac{{\rm d}}{{\rm d}z}-2T\right)\left(l\frac{{\rm d}}{{\rm d}z}-T\right){\rm e}^{uz/4}\nonumber\\ &=\mathrm{e}^{uz/4}\{[{-}15u^4+(420S^2-225)u^2-945S^4+840S^2-120]T\nonumber\\ &\quad +u[u^4+({-}105S^2+85)u^2+(945S^4-1155S^2+274)]\}, \end{align}
which is exactly (2.2). When the boundary conditions require 
$|u\rangle$ to be bounded at 
$|z| \to \infty$, and 
$u$ is real, the polynomial obtained by letting 
$S\to 0$ and 
$T\to \textrm {sign}(z)$ must be zero, which restricts the real values of 
$u$ to that polynomial's roots. These are the first five positive integers and give the discrete modes. Imaginary 
$u$ values give finite 
$|u\rangle$ at infinity and are not restricted except by parity considerations: they are the continuum modes. Evidently the same process can be used to find the adiabatic eigenmodes of any potential of the form 
${\,{\rm sech}}^{l}(z/l)$ with 
$0< l=(n-1)\in \boldsymbol {Z}$. Such a potential has 
$l+1$ discrete modes.
