1 Introduction
Edge localised modes (ELMs) are a ubiquitous feature of H-mode tokamak plasmas with important consequences for confinement and for transient heat loads on divertor target plates. Most theoretical models appeal to ideal magnetohydrodynamic (MHD) ballooning and peeling modes (Hegna et al. Reference Hegna, Connor, Hastie and Wilson1996; Connor et al. Reference Connor, Hastie, Wilson and Miller1998; Wilson et al. Reference Wilson, Connor, Field, Fielding, Miller, Lao, Ferron and Turnbull1999; Snyder et al. Reference Snyder, Wilson, Ferron, Lao, Leonard, Mossessian, Murakami, Osborne, Turnbull and Xu2004) as the trigger for ELMs. While this may well be the case for larger Type I ELMs, the smaller Type III may involve resistive ballooning modes (Connor Reference Connor1998). Furthermore it is unclear whether ideal peeling modes are ever unstable due to the presence of a separatrix in divertor tokamaks (Huysmans Reference Huysmans2005; Webster & Gimblett Reference Webster and Gimblett2009) or can lead to the required destruction of magnetic surfaces seen in resistive MHD simulations, e.g. ASDEX Team (Reference ASDEX Team1989). However, concerning the need for resistivity, one should mention a model for ELMs in which an unstable ideal peeling mode does play a part, triggering a Taylor relaxation in the edge plasma, thus involving reconnection. The relaxation region grows in size until the ideal mode becomes stable (Gimblett, Hastie & Helander Reference Gimblett, Hastie and Helander2006). An alternative possible explanation is that ELMs might be triggered by tearing modes being driven unstable by the large bootstrap current density that results from the pressure gradients in the H-mode pedestal.
The theory of tearing modes utilises asymptotic matching techniques (Furth, Killeen & Rosenbluth Reference Furth, Killeen and Rosenbluth1963). Thus solutions of the resistive equations (or those corresponding to more complex plasma models e.g. Antonsen & Coppi (Reference Antonsen and Coppi1981), Drake et al. (Reference Drake, Antonsen, Hassam and Gladd1983), Cowley, Kulsrud & Hahm (Reference Cowley, Kulsrud and Hahm1986), Pegoraro & Schep (Reference Pegoraro and Schep1986), Porcelli (Reference Porcelli1987), Fitzpatrick (Reference Fitzpatrick1989), Connor, Hastie & Zocco (Reference Connor, Hastie and Zocco2012)) that pertain near resonant surfaces,
![]() $m=nq(\unicode[STIX]{x1D70C}_{s})$
, are matched to solutions of ideal MHD equations that describe the regions away from the resonance to obtain a dispersion relation determining their stability. Here
$m=nq(\unicode[STIX]{x1D70C}_{s})$
, are matched to solutions of ideal MHD equations that describe the regions away from the resonance to obtain a dispersion relation determining their stability. Here
![]() $m$
and
$m$
and
![]() $n$
are poloidal and toroidal mode numbers of the perturbation,
$n$
are poloidal and toroidal mode numbers of the perturbation,
![]() $q(\unicode[STIX]{x1D70C})$
is the safety factor,
$q(\unicode[STIX]{x1D70C})$
is the safety factor,
![]() $\unicode[STIX]{x1D70C}$
is a flux surface label with dimensions of length and
$\unicode[STIX]{x1D70C}$
is a flux surface label with dimensions of length and
![]() $\unicode[STIX]{x1D70C}_{s}$
is the resonance position. This matching procedure involves obtaining the asymptotic forms of the ideal MHD solutions as
$\unicode[STIX]{x1D70C}_{s}$
is the resonance position. This matching procedure involves obtaining the asymptotic forms of the ideal MHD solutions as
![]() $\unicode[STIX]{x1D70C}\rightarrow \unicode[STIX]{x1D70C}_{s}$
from both left and right, and the matching is characterised by a quantity
$\unicode[STIX]{x1D70C}\rightarrow \unicode[STIX]{x1D70C}_{s}$
from both left and right, and the matching is characterised by a quantity
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
. Stability of a mode is determined by comparing
$\unicode[STIX]{x1D6E5}^{\prime }$
. Stability of a mode is determined by comparing
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
with
$\unicode[STIX]{x1D6E5}^{\prime }$
with
![]() $\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
, a parameter that is determined from the solution of the equation describing the narrow layer around the resonance. The quantity
$\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
, a parameter that is determined from the solution of the equation describing the narrow layer around the resonance. The quantity
![]() $\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
is usually a large positive number (Glasser, Greene & Johnson Reference Glasser, Greene and Johnson1975; Drake et al.
Reference Drake, Antonsen, Hassam and Gladd1983; Cowley et al.
Reference Cowley, Kulsrud and Hahm1986), but physics close to the resonance can make
$\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
is usually a large positive number (Glasser, Greene & Johnson Reference Glasser, Greene and Johnson1975; Drake et al.
Reference Drake, Antonsen, Hassam and Gladd1983; Cowley et al.
Reference Cowley, Kulsrud and Hahm1986), but physics close to the resonance can make
![]() $\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
negative: e.g. when microtearing modes are unstable, as has been reported for the plasma region around the H-mode pedestal in the Mega Ampère Spherical Tokamak (MAST) (Dickinson et al.
Reference Dickinson, Roach, Saarelma, Scannell, Kirk and Wilson2012) and in the Joint European Torus (JET) (Hatch et al.
Reference Hatch, Kotschenreuther, Mahajan, Valanju, Jenko, Told, Görler and Saarelma2016).
$\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
negative: e.g. when microtearing modes are unstable, as has been reported for the plasma region around the H-mode pedestal in the Mega Ampère Spherical Tokamak (MAST) (Dickinson et al.
Reference Dickinson, Roach, Saarelma, Scannell, Kirk and Wilson2012) and in the Joint European Torus (JET) (Hatch et al.
Reference Hatch, Kotschenreuther, Mahajan, Valanju, Jenko, Told, Görler and Saarelma2016).
The linear theory of tearing instability in toroidal geometry (Connor et al.
Reference Connor, Cowley, Hastie, Hender, Hood and Martin1988) is a complex problem, raising issues associated with the coupling of different poloidal harmonics and with the decoupling of resonances at different rational surfaces due to differing diamagnetic frequencies at such surfaces. Hegna & Callen (Reference Hegna and Callen1994) proposed a simple approximation that the perturbed poloidal flux has a single poloidal harmonic, of admittedly uncertain accuracy, to obtain a master equation for tearing instability, with similar one-dimensional (1-D) character to that holding in a straight cylinder. This equation was derived for equilibria with weakly shaped poloidal cross-section, and under the additional assumptions of large aspect ratio, low
![]() $\unicode[STIX]{x1D6FD}$
(where
$\unicode[STIX]{x1D6FD}$
(where
![]() $\unicode[STIX]{x1D6FD}$
is the ratio of plasma pressure,
$\unicode[STIX]{x1D6FD}$
is the ratio of plasma pressure,
![]() $p$
, to the magnetic field energy density,
$p$
, to the magnetic field energy density,
![]() $\unicode[STIX]{x1D6FD}=2\unicode[STIX]{x1D707}_{0}p/B^{2}$
) and with the toroidal magnetic field greatly exceeding the poloidal field:
$\unicode[STIX]{x1D6FD}=2\unicode[STIX]{x1D707}_{0}p/B^{2}$
) and with the toroidal magnetic field greatly exceeding the poloidal field:
where
![]() $\tilde{A}$
and
$\tilde{A}$
and
![]() $\unicode[STIX]{x1D713}$
are respectively the perturbed and equilibrium poloidal flux, the magnetic field is
$\unicode[STIX]{x1D713}$
are respectively the perturbed and equilibrium poloidal flux, the magnetic field is
![]() $\boldsymbol{B}=I\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}+\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
,
$\boldsymbol{B}=I\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}+\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
,
![]() $I$
is the toroidal field function
$I$
is the toroidal field function
![]() $I=RB_{\unicode[STIX]{x1D719}}$
,
$I=RB_{\unicode[STIX]{x1D719}}$
,
![]() $\unicode[STIX]{x1D719}$
is the toroidal coordinate,
$\unicode[STIX]{x1D719}$
is the toroidal coordinate,
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D707}_{0}j_{\Vert }/B$
, with the parallel current density
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D707}_{0}j_{\Vert }/B$
, with the parallel current density
![]() $j_{\Vert }=\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{B}/B$
,
$j_{\Vert }=\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{B}/B$
,
![]() $q$
is the safety factor,
$q$
is the safety factor,
![]() $^{\prime }$
denotes the radial gradient with respect to
$^{\prime }$
denotes the radial gradient with respect to
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $\langle Y\rangle$
is the flux surface average of
$\langle Y\rangle$
is the flux surface average of
![]() $Y$
for any quantity
$Y$
for any quantity
![]() $Y(\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
,
$Y(\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
,
and the metric elements are
![]() $g^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D713}}=|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}$
and
$g^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D713}}=|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}$
and
![]() $g^{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}=|\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}|^{2}$
. The
$g^{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}=|\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}|^{2}$
. The
![]() $\unicode[STIX]{x1D703}$
coordinate is a straight field line poloidal angle and
$\unicode[STIX]{x1D703}$
coordinate is a straight field line poloidal angle and
![]() $J=(\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719})^{-1}=R^{2}q/I$
is the Jacobian. Nishimura, Callen & Hegna (Reference Nishimura, Callen and Hegna1998) presented numerical solutions of a similar equation, for a family of equilibrium profiles resembling those studied previously by Furth, Rutherford & Selberg (Reference Furth, Rutherford and Selberg1973) in a cylindrical geometry.
$J=(\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719})^{-1}=R^{2}q/I$
is the Jacobian. Nishimura, Callen & Hegna (Reference Nishimura, Callen and Hegna1998) presented numerical solutions of a similar equation, for a family of equilibrium profiles resembling those studied previously by Furth, Rutherford & Selberg (Reference Furth, Rutherford and Selberg1973) in a cylindrical geometry.
To assist the tearing mode stability analysis of the H-mode pedestal, in this paper we develop a 1-D ideal MHD equation for application to realistic, fully toroidal tokamak equilibria at high
![]() $\unicode[STIX]{x1D6FD}$
, thus generalising the earlier seminal works by Hegna & Callen (Reference Hegna and Callen1994) and Nishimura et al. (Reference Nishimura, Callen and Hegna1998). This contrasts with alternative approximate treatments described in Fitzpatrick et al. (Reference Fitzpatrick, Hastie, Martin and Roach1993), where the effect of poloidal mode coupling was calculated for toroidal equilibria of large aspect ratio, low
$\unicode[STIX]{x1D6FD}$
, thus generalising the earlier seminal works by Hegna & Callen (Reference Hegna and Callen1994) and Nishimura et al. (Reference Nishimura, Callen and Hegna1998). This contrasts with alternative approximate treatments described in Fitzpatrick et al. (Reference Fitzpatrick, Hastie, Martin and Roach1993), where the effect of poloidal mode coupling was calculated for toroidal equilibria of large aspect ratio, low
![]() $\unicode[STIX]{x1D6FD}$
and weak shaping, and approximate solutions with seven poloidal harmonics were used to obtain
$\unicode[STIX]{x1D6FD}$
and weak shaping, and approximate solutions with seven poloidal harmonics were used to obtain
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
.
$\unicode[STIX]{x1D6E5}^{\prime }$
.
2 A 1-D tearing mode equation
We start from equations (A5) and (A6) of Connor et al. (Reference Connor, Cowley, Hastie, Hender, Hood and Martin1988), which respectively govern the radial component of the displacement (
![]() $\unicode[STIX]{x1D743}$
), and the perturbed toroidal magnetic field: these quantities manifest themselves in Connor et al.’s variables
$\unicode[STIX]{x1D743}$
), and the perturbed toroidal magnetic field: these quantities manifest themselves in Connor et al.’s variables
![]() $y=R_{0}f\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
and
$y=R_{0}f\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
and
![]() $z=R^{2}\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}/B_{0}$
. Here the equilibrium magnetic field is written as
$z=R^{2}\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}/B_{0}$
. Here the equilibrium magnetic field is written as
![]() $\boldsymbol{B}=R_{0}B_{0}[g\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}+f\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}]$
, where
$\boldsymbol{B}=R_{0}B_{0}[g\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}+f\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}]$
, where
![]() $\unicode[STIX]{x1D70C}$
is a flux surface label with dimension of length,
$\unicode[STIX]{x1D70C}$
is a flux surface label with dimension of length,
![]() $B_{0}g(\unicode[STIX]{x1D70C})R_{0}/R$
is the full toroidal magnetic field,
$B_{0}g(\unicode[STIX]{x1D70C})R_{0}/R$
is the full toroidal magnetic field,
![]() $B_{0}$
is the vacuum toroidal field at the major radius,
$B_{0}$
is the vacuum toroidal field at the major radius,
![]() $R_{0}$
, of the magnetic axis and
$R_{0}$
, of the magnetic axis and
![]() $q=(\unicode[STIX]{x1D70C}/R_{0})(g/f)$
. The variable
$q=(\unicode[STIX]{x1D70C}/R_{0})(g/f)$
. The variable
![]() $y$
, which is related to the perturbed poloidal flux, now denoted
$y$
, which is related to the perturbed poloidal flux, now denoted
![]() $\unicode[STIX]{x1D713}$
, by
$\unicode[STIX]{x1D713}$
, by
![]() $y=\unicode[STIX]{x1D713}/(m-nq)$
,Footnote
1
is assumed to contain only a single poloidal harmonic,
$y=\unicode[STIX]{x1D713}/(m-nq)$
,Footnote
1
is assumed to contain only a single poloidal harmonic,
![]() $\text{e}^{\text{i}m\unicode[STIX]{x1D703}}$
, where
$\text{e}^{\text{i}m\unicode[STIX]{x1D703}}$
, where
![]() $\unicode[STIX]{x1D703}$
is the poloidal angle in straight field line coordinates. These equations can be used to generate the 1-D ideal MHD equation for
$\unicode[STIX]{x1D703}$
is the poloidal angle in straight field line coordinates. These equations can be used to generate the 1-D ideal MHD equation for
![]() $\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x1D713}$
.
Then equations (A5) and (A6) of Connor et al. (Reference Connor, Cowley, Hastie, Hender, Hood and Martin1988) take the form
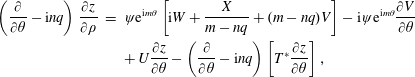 $$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}-\text{i}nq\right)\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}} & = & \displaystyle \unicode[STIX]{x1D713}\text{e}^{\text{i}m\unicode[STIX]{x1D703}}\left[\text{i}W+\frac{X}{m-nq}+(m-nq)V\right]-\text{i}\unicode[STIX]{x1D713}\text{e}^{\text{i}m\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,U\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}-\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}-\text{i}nq\right)\left[T^{\ast }\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}-\text{i}nq\right)\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}} & = & \displaystyle \unicode[STIX]{x1D713}\text{e}^{\text{i}m\unicode[STIX]{x1D703}}\left[\text{i}W+\frac{X}{m-nq}+(m-nq)V\right]-\text{i}\unicode[STIX]{x1D713}\text{e}^{\text{i}m\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,U\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}-\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}-\text{i}nq\right)\left[T^{\ast }\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right],\end{eqnarray}$$
where the equilibrium quantities,
![]() $Q,S,T,U,V,W,X$
are defined in equation (A7) of Connor et al. (Reference Connor, Cowley, Hastie, Hender, Hood and Martin1988),
$Q,S,T,U,V,W,X$
are defined in equation (A7) of Connor et al. (Reference Connor, Cowley, Hastie, Hender, Hood and Martin1988),
with
![]() $^{\prime }$
now representing the radial derivative with respect to
$^{\prime }$
now representing the radial derivative with respect to
![]() $\unicode[STIX]{x1D70C}$
. We note here that the above expressions were derived for equilibria of arbitrary aspect ratio, cross-sectional shape and
$\unicode[STIX]{x1D70C}$
. We note here that the above expressions were derived for equilibria of arbitrary aspect ratio, cross-sectional shape and
![]() $\unicode[STIX]{x1D6FD}$
. The method employed in the following analysis is rather general and does not assume that the second dependent variable,
$\unicode[STIX]{x1D6FD}$
. The method employed in the following analysis is rather general and does not assume that the second dependent variable,
![]() $z$
, is also of single poloidal harmonic structure.
$z$
, is also of single poloidal harmonic structure.
To simplify the analysis we neglect the term involving
![]() $S$
, relative to
$S$
, relative to
![]() $m^{2}Q$
in (2.1). This is equivalent to reducing the field line bending energy in a circular cylinder from the
$m^{2}Q$
in (2.1). This is equivalent to reducing the field line bending energy in a circular cylinder from the
![]() $(m^{2}+k_{z}^{2}r^{2})$
of the Newcomb (Reference Newcomb1960) analysis of stability in a linear pinch, to
$(m^{2}+k_{z}^{2}r^{2})$
of the Newcomb (Reference Newcomb1960) analysis of stability in a linear pinch, to
![]() $m^{2}$
. In a torus this is equivalent to an assumption that
$m^{2}$
. In a torus this is equivalent to an assumption that
![]() $(\unicode[STIX]{x1D716}/q_{s})^{2}\ll 1$
, where
$(\unicode[STIX]{x1D716}/q_{s})^{2}\ll 1$
, where
![]() $\unicode[STIX]{x1D716}$
is the local aspect ratio and
$\unicode[STIX]{x1D716}$
is the local aspect ratio and
![]() $q_{s}=m/n$
is the value of the safety factor at the resonance. Since our focus will be on tearing modes which are resonant in the pedestal region of a tokamak of aspect ratio around
$q_{s}=m/n$
is the value of the safety factor at the resonance. Since our focus will be on tearing modes which are resonant in the pedestal region of a tokamak of aspect ratio around
![]() $1/3$
,
$1/3$
,
![]() $q_{s}$
may be of order
$q_{s}$
may be of order
![]() $4$
or greater, so this approximation would appear to introduce errors of only approximately
$4$
or greater, so this approximation would appear to introduce errors of only approximately
![]() $1\,\%$
.
$1\,\%$
.
The required 1-D tearing equation is now obtained by solving (2.1) for
![]() $\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}$
, inserting the result in (2.2) and taking the flux surface average. Thus:
$\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}$
, inserting the result in (2.2) and taking the flux surface average. Thus:
where
![]() $K(\unicode[STIX]{x1D70C})$
is a flux surface dependent constant of integration to be determined by a periodicity constraint on
$K(\unicode[STIX]{x1D70C})$
is a flux surface dependent constant of integration to be determined by a periodicity constraint on
![]() $z(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703})$
. Thus
$z(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703})$
. Thus
with
where the second form in (2.12)–(2.14) applies for equilibria which are symmetric above and below the median plane. Now, since the
![]() $m$
number for tearing modes which are resonant in the pedestal region of a tokamak is likely to be moderately large, the coefficients defined by
$m$
number for tearing modes which are resonant in the pedestal region of a tokamak is likely to be moderately large, the coefficients defined by
![]() $\unicode[STIX]{x1D6FC}_{m},\unicode[STIX]{x1D6FE}_{m}$
and
$\unicode[STIX]{x1D6FC}_{m},\unicode[STIX]{x1D6FE}_{m}$
and
![]() $\unicode[STIX]{x1D6FF}_{m}$
in (2.12)–(2.14) may be very small unless there is strong shaping. Consequently, we can normally neglect the integration constant,
$\unicode[STIX]{x1D6FF}_{m}$
in (2.12)–(2.14) may be very small unless there is strong shaping. Consequently, we can normally neglect the integration constant,
![]() $K(\unicode[STIX]{x1D70C})$
defined in (2.11). In § 2.1 we will investigate the consequences of retaining finite
$K(\unicode[STIX]{x1D70C})$
defined in (2.11). In § 2.1 we will investigate the consequences of retaining finite
![]() $K(\unicode[STIX]{x1D70C})$
.
$K(\unicode[STIX]{x1D70C})$
.
Inserting the expression for
![]() $(\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})$
(in the
$(\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})$
(in the
![]() $K(\unicode[STIX]{x1D70C})=0$
limit) into (2.2) and multiplying by the factor
$K(\unicode[STIX]{x1D70C})=0$
limit) into (2.2) and multiplying by the factor
![]() $\text{e}^{-\text{i}m\unicode[STIX]{x1D703}}$
, we take the flux surface average to obtain a 1-D tearing mode equation. Expressed in terms of the equilibrium quantities,
$\text{e}^{-\text{i}m\unicode[STIX]{x1D703}}$
, we take the flux surface average to obtain a 1-D tearing mode equation. Expressed in terms of the equilibrium quantities,
![]() $Q,T,U,V,W$
and
$Q,T,U,V,W$
and
![]() $X$
, this takes the form:
$X$
, this takes the form:
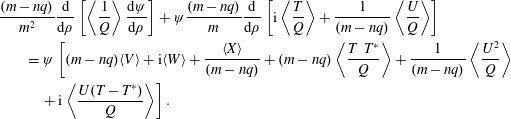 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(m-nq)}{m^{2}}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left[\left\langle \frac{1}{Q}\right\rangle \frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}\unicode[STIX]{x1D70C}}\right]+\unicode[STIX]{x1D713}\frac{(m-nq)}{m}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left[\text{i}\left\langle \frac{T}{Q}\right\rangle +\frac{1}{(m-nq)}\left\langle \frac{U}{Q}\right\rangle \right]\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D713}\left[(m-nq)\langle V\rangle +\text{i}\langle W\rangle +\frac{\langle X\rangle }{(m-nq)}+(m-nq)\left\langle \frac{T~T^{\ast }}{Q}\right\rangle +\frac{1}{(m-nq)}\left\langle \frac{U^{2}}{Q}\right\rangle \right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,\text{i}\left\langle \frac{U(T-T^{\ast })}{Q}\right\rangle \right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(m-nq)}{m^{2}}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left[\left\langle \frac{1}{Q}\right\rangle \frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}\unicode[STIX]{x1D70C}}\right]+\unicode[STIX]{x1D713}\frac{(m-nq)}{m}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left[\text{i}\left\langle \frac{T}{Q}\right\rangle +\frac{1}{(m-nq)}\left\langle \frac{U}{Q}\right\rangle \right]\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D713}\left[(m-nq)\langle V\rangle +\text{i}\langle W\rangle +\frac{\langle X\rangle }{(m-nq)}+(m-nq)\left\langle \frac{T~T^{\ast }}{Q}\right\rangle +\frac{1}{(m-nq)}\left\langle \frac{U^{2}}{Q}\right\rangle \right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,\text{i}\left\langle \frac{U(T-T^{\ast })}{Q}\right\rangle \right].\end{eqnarray}$$
Now, writing
![]() $1/Q=\unicode[STIX]{x1D706}\unicode[STIX]{x1D70C}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}$
, where
$1/Q=\unicode[STIX]{x1D706}\unicode[STIX]{x1D70C}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}$
, where
![]() $\unicode[STIX]{x1D706}=\text{i}n/R_{0}$
and dividing through by
$\unicode[STIX]{x1D706}=\text{i}n/R_{0}$
and dividing through by
![]() $\unicode[STIX]{x1D706}(m-nq)/m^{2}$
, equation (2.15) takes the form of the second order differential equation:
$\unicode[STIX]{x1D706}(m-nq)/m^{2}$
, equation (2.15) takes the form of the second order differential equation:
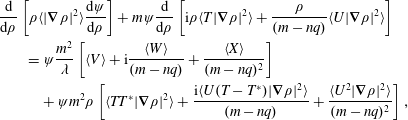 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left[\unicode[STIX]{x1D70C}\langle |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle \frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}\unicode[STIX]{x1D70C}}\right]+m\unicode[STIX]{x1D713}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left[\text{i}\unicode[STIX]{x1D70C}\langle T|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle +\frac{\unicode[STIX]{x1D70C}}{(m-nq)}\langle U|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle \right]\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D713}\frac{m^{2}}{\unicode[STIX]{x1D706}}\left[\langle V\rangle +\text{i}\frac{\langle W\rangle }{(m-nq)}+\frac{\langle X\rangle }{(m-nq)^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\unicode[STIX]{x1D713}m^{2}\unicode[STIX]{x1D70C}\left[\langle TT^{\ast }|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle +\frac{\text{i}\langle U(T-T^{\ast })|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle }{(m-nq)}+\frac{\langle U^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle }{(m-nq)^{2}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left[\unicode[STIX]{x1D70C}\langle |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle \frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}\unicode[STIX]{x1D70C}}\right]+m\unicode[STIX]{x1D713}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left[\text{i}\unicode[STIX]{x1D70C}\langle T|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle +\frac{\unicode[STIX]{x1D70C}}{(m-nq)}\langle U|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle \right]\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D713}\frac{m^{2}}{\unicode[STIX]{x1D706}}\left[\langle V\rangle +\text{i}\frac{\langle W\rangle }{(m-nq)}+\frac{\langle X\rangle }{(m-nq)^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\unicode[STIX]{x1D713}m^{2}\unicode[STIX]{x1D70C}\left[\langle TT^{\ast }|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle +\frac{\text{i}\langle U(T-T^{\ast })|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle }{(m-nq)}+\frac{\langle U^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}\rangle }{(m-nq)^{2}}\right],\end{eqnarray}$$
which is of the same structure as the equation derived by Hegna & Callen (Reference Hegna and Callen1994), namely
where, on inserting the definitions (2.4)–(2.9),
Some details of the derivation of (2.18)–(2.21) are given in appendix A, and in appendix B we express equation (2.17) in terms of the variables used in equation (26) of Hegna & Callen (Reference Hegna and Callen1994).
2.1 Consequences of finite K
We now return to (2.10) and (2.11) and construct the additional terms that will appear in the tearing equation when we retain terms with finite
![]() $K(\unicode[STIX]{x1D70C})$
. After lengthy, but straightforward, further analysis, we find that each of the coefficients
$K(\unicode[STIX]{x1D70C})$
. After lengthy, but straightforward, further analysis, we find that each of the coefficients
![]() $A(\unicode[STIX]{x1D70C}),B(\unicode[STIX]{x1D70C}),C(\unicode[STIX]{x1D70C})$
and
$A(\unicode[STIX]{x1D70C}),B(\unicode[STIX]{x1D70C}),C(\unicode[STIX]{x1D70C})$
and
![]() $D(\unicode[STIX]{x1D70C})$
is modified by an additional contribution, which we shall denote by a circumflex. Thus
$D(\unicode[STIX]{x1D70C})$
is modified by an additional contribution, which we shall denote by a circumflex. Thus
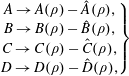 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}A\rightarrow A(\unicode[STIX]{x1D70C})-\hat{A}(\unicode[STIX]{x1D70C}),\\ B\rightarrow B(\unicode[STIX]{x1D70C})-\hat{B}(\unicode[STIX]{x1D70C}),\\ C\rightarrow C(\unicode[STIX]{x1D70C})-{\hat{C}}(\unicode[STIX]{x1D70C}),\\ D\rightarrow D(\unicode[STIX]{x1D70C})-\hat{D}(\unicode[STIX]{x1D70C}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}A\rightarrow A(\unicode[STIX]{x1D70C})-\hat{A}(\unicode[STIX]{x1D70C}),\\ B\rightarrow B(\unicode[STIX]{x1D70C})-\hat{B}(\unicode[STIX]{x1D70C}),\\ C\rightarrow C(\unicode[STIX]{x1D70C})-{\hat{C}}(\unicode[STIX]{x1D70C}),\\ D\rightarrow D(\unicode[STIX]{x1D70C})-\hat{D}(\unicode[STIX]{x1D70C}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
with
where
![]() $s=\unicode[STIX]{x1D70C}q^{\prime }/qs=\unicode[STIX]{x1D70C}q^{\prime }/q$
is the magnetic shear.
$s=\unicode[STIX]{x1D70C}q^{\prime }/qs=\unicode[STIX]{x1D70C}q^{\prime }/q$
is the magnetic shear.
![]() $\hat{A}$
,
$\hat{A}$
,
![]() $\hat{B}$
,
$\hat{B}$
,
![]() ${\hat{C}}$
and
${\hat{C}}$
and
![]() $\hat{D}$
are small in the large
$\hat{D}$
are small in the large
![]() $m$
limit because the numerators in the definitions of
$m$
limit because the numerators in the definitions of
![]() $\unicode[STIX]{x1D6FC}_{m}$
,
$\unicode[STIX]{x1D6FC}_{m}$
,
![]() $\unicode[STIX]{x1D6FF}_{m}$
,
$\unicode[STIX]{x1D6FF}_{m}$
,
![]() $\unicode[STIX]{x1D6FE}_{m}$
(see (2.12)–(2.14)) must vanish both at high
$\unicode[STIX]{x1D6FE}_{m}$
(see (2.12)–(2.14)) must vanish both at high
![]() $m$
, or with weak shaping. At a fixed finite
$m$
, or with weak shaping. At a fixed finite
![]() $m$
these terms can, however, become more important with stronger shaping (e.g. as one approaches the separatrix).
$m$
these terms can, however, become more important with stronger shaping (e.g. as one approaches the separatrix).
2.2 Comparison with earlier results
The Hegna–Callen equation represented a significant advance on earlier work by making possible a simple 1-D tearing analysis of large aspect ratio toroidal equilibria with weakly shaped poloidal cross-sections. Our derivation has not only extended the validity of the 1-D equation to finite aspect ratio equilibria, subject to
![]() $(\unicode[STIX]{x1D716}/q_{s})^{2}\ll 1$
, with arbitrary poloidal shaping, but it has also revealed the presence of new terms arising from finite values of the integration constant
$(\unicode[STIX]{x1D716}/q_{s})^{2}\ll 1$
, with arbitrary poloidal shaping, but it has also revealed the presence of new terms arising from finite values of the integration constant
![]() $K(\unicode[STIX]{x1D70C})$
. These additional terms of (2.23)–(2.26) have no counterpart in Hegna & Callen (Reference Hegna and Callen1994) or Nishimura et al. (Reference Nishimura, Callen and Hegna1998), but they are small unless there is strong shaping containing poloidal harmonics that couple to the mode number,
$K(\unicode[STIX]{x1D70C})$
. These additional terms of (2.23)–(2.26) have no counterpart in Hegna & Callen (Reference Hegna and Callen1994) or Nishimura et al. (Reference Nishimura, Callen and Hegna1998), but they are small unless there is strong shaping containing poloidal harmonics that couple to the mode number,
![]() $m$
.
$m$
.
We now compare our tearing equation (2.17) with Hegna & Callen (Reference Hegna and Callen1994) and Nishimura et al. (Reference Nishimura, Callen and Hegna1998). We begin by transforming from the Hegna–Callen equilibrium variables,
![]() $I$
and
$I$
and
![]() $\unicode[STIX]{x1D713}$
, to the
$\unicode[STIX]{x1D713}$
, to the
![]() $g,f,\unicode[STIX]{x1D70C}$
variables of the present work. Thus:
$g,f,\unicode[STIX]{x1D70C}$
variables of the present work. Thus:
The coefficients
![]() $A,B,C$
and
$A,B,C$
and
![]() $D$
can then be identified in equation (26) of Hegna & Callen (Reference Hegna and Callen1994) and compared to (2.18)–(2.21). This shows agreement in the expressions for
$D$
can then be identified in equation (26) of Hegna & Callen (Reference Hegna and Callen1994) and compared to (2.18)–(2.21). This shows agreement in the expressions for
![]() $A$
and
$A$
and
![]() $B$
, close agreement on
$B$
, close agreement on
![]() $C$
, but not for
$C$
, but not for
![]() $D$
. Since
$D$
. Since
one can indeed write
![]() $C\propto (\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70E}\rangle /\unicode[STIX]{x2202}\unicode[STIX]{x1D70C})$
if
$C\propto (\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70E}\rangle /\unicode[STIX]{x2202}\unicode[STIX]{x1D70C})$
if
![]() $B\simeq B_{\unicode[STIX]{x1D719}}$
, as in Hegna & Callen (Reference Hegna and Callen1994). There is some similarity with the expression for
$B\simeq B_{\unicode[STIX]{x1D719}}$
, as in Hegna & Callen (Reference Hegna and Callen1994). There is some similarity with the expression for
![]() $D$
that appears in equation (19) of Nishimura et al. (Reference Nishimura, Callen and Hegna1998), where special equilibria with
$D$
that appears in equation (19) of Nishimura et al. (Reference Nishimura, Callen and Hegna1998), where special equilibria with
![]() $g=$
constant were studied so that the last term in (2.21) is absent, but nevertheless their
$g=$
constant were studied so that the last term in (2.21) is absent, but nevertheless their
![]() $D\propto n^{2}q^{2}$
rather than
$D\propto n^{2}q^{2}$
rather than
![]() $m^{2}$
, and so it differs away from the resonance.
$m^{2}$
, and so it differs away from the resonance.
As noted by Hegna, Callen and Nishimura, there is an important comparison for the expression given in (2.21) for
![]() $D(\unicode[STIX]{x1D70C})$
. This is associated with the Mercier stability criterion,
$D(\unicode[STIX]{x1D70C})$
. This is associated with the Mercier stability criterion,
![]() $D_{M}<0$
, for the ideal MHD stability of a mode localised around a rational surface (Mercier Reference Mercier1960). Glasser et al. (Reference Glasser, Greene and Johnson1975) showed
$D_{M}<0$
, for the ideal MHD stability of a mode localised around a rational surface (Mercier Reference Mercier1960). Glasser et al. (Reference Glasser, Greene and Johnson1975) showed
![]() $D_{M}$
Footnote
2
plays an important role in the theory of tearing mode stability in a torus. They found the asymptotic form of the ideal MHD solutions as
$D_{M}$
Footnote
2
plays an important role in the theory of tearing mode stability in a torus. They found the asymptotic form of the ideal MHD solutions as
![]() $\unicode[STIX]{x1D70C}\rightarrow \unicode[STIX]{x1D70C}_{s}$
is
$\unicode[STIX]{x1D70C}\rightarrow \unicode[STIX]{x1D70C}_{s}$
is
where
![]() $x=\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{s}$
, constants
$x=\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{s}$
, constants
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
have different values to the left and right of the resonance, and the Mercier indices
$c_{1}$
have different values to the left and right of the resonance, and the Mercier indices
![]() $\unicode[STIX]{x1D708}_{\pm }$
have values:
$\unicode[STIX]{x1D708}_{\pm }$
have values:
This serves to define a generalised
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
$\unicode[STIX]{x1D6E5}^{\prime }$
where
![]() $R$
and
$R$
and
![]() $L$
denote locations immediately to the right and left of the resonance, respectively. This expression, obtained from the ideal MHD solution, must be matched to the analogous quantity arising from the inner resonant layer solution, to obtain the tearing mode dispersion relation.
$L$
denote locations immediately to the right and left of the resonance, respectively. This expression, obtained from the ideal MHD solution, must be matched to the analogous quantity arising from the inner resonant layer solution, to obtain the tearing mode dispersion relation.
Using the results in Glasser et al. (Reference Glasser, Greene and Johnson1975) and Connor et al. (Reference Connor, Cowley, Hastie, Hender, Hood and Martin1988)Footnote
3
we find that, at the tearing mode resonance,
![]() $D$
of (2.21) should be compared to
$D$
of (2.21) should be compared to
![]() $-(As^{2}/\unicode[STIX]{x1D70C}^{2})((1/4)+D_{M})$
, where
$-(As^{2}/\unicode[STIX]{x1D70C}^{2})((1/4)+D_{M})$
, where
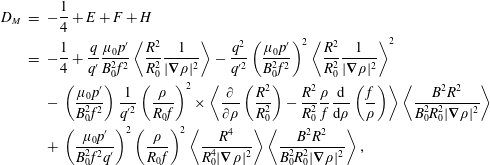 $$\begin{eqnarray}\displaystyle D_{M} & = & \displaystyle -\frac{1}{4}+E+F+H\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{4}+\frac{q}{q^{\prime }}\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{B_{0}^{2}f^{2}}\left\langle \frac{R^{2}}{R_{0}^{2}}\frac{1}{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle -\frac{q^{2}}{q^{\prime 2}}\left(\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{B_{0}^{2}f^{2}}\right)^{2}\left\langle \frac{R^{2}}{R_{0}^{2}}\frac{1}{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle ^{2}\nonumber\\ \displaystyle & & \displaystyle -\,\left(\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{B_{0}^{2}f^{2}}\right)\frac{1}{q^{\prime 2}}\left(\frac{\unicode[STIX]{x1D70C}}{R_{0}f}\right)^{2}\times \left\langle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\left(\frac{R^{2}}{R_{0}^{2}}\right)-\frac{R^{2}}{R_{0}^{2}}\frac{\unicode[STIX]{x1D70C}}{f}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left(\frac{f}{\unicode[STIX]{x1D70C}}\right)\right\rangle \left\langle \frac{B^{2}R^{2}}{B_{0}^{2}R_{0}^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{B_{0}^{2}f^{2}q^{\prime }}\right)^{2}\left(\frac{\unicode[STIX]{x1D70C}}{R_{0}f}\right)^{2}\left\langle \frac{R^{4}}{R_{0}^{4}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle \left\langle \frac{B^{2}R^{2}}{B_{0}^{2}R_{0}^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{M} & = & \displaystyle -\frac{1}{4}+E+F+H\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{4}+\frac{q}{q^{\prime }}\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{B_{0}^{2}f^{2}}\left\langle \frac{R^{2}}{R_{0}^{2}}\frac{1}{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle -\frac{q^{2}}{q^{\prime 2}}\left(\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{B_{0}^{2}f^{2}}\right)^{2}\left\langle \frac{R^{2}}{R_{0}^{2}}\frac{1}{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle ^{2}\nonumber\\ \displaystyle & & \displaystyle -\,\left(\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{B_{0}^{2}f^{2}}\right)\frac{1}{q^{\prime 2}}\left(\frac{\unicode[STIX]{x1D70C}}{R_{0}f}\right)^{2}\times \left\langle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\left(\frac{R^{2}}{R_{0}^{2}}\right)-\frac{R^{2}}{R_{0}^{2}}\frac{\unicode[STIX]{x1D70C}}{f}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70C}}\left(\frac{f}{\unicode[STIX]{x1D70C}}\right)\right\rangle \left\langle \frac{B^{2}R^{2}}{B_{0}^{2}R_{0}^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{B_{0}^{2}f^{2}q^{\prime }}\right)^{2}\left(\frac{\unicode[STIX]{x1D70C}}{R_{0}f}\right)^{2}\left\langle \frac{R^{4}}{R_{0}^{4}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle \left\langle \frac{B^{2}R^{2}}{B_{0}^{2}R_{0}^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}}\right\rangle ,\end{eqnarray}$$
and the quantities
![]() $E,~F$
and
$E,~F$
and
![]() $H$
are defined in Glasser et al. (Reference Glasser, Greene and Johnson1975). (In a later paper, Glasser, Greene & Johnson (Reference Glasser, Greene and Johnson1976) showed that for a large aspect ratio circular cross-section plasma:
$H$
are defined in Glasser et al. (Reference Glasser, Greene and Johnson1975). (In a later paper, Glasser, Greene & Johnson (Reference Glasser, Greene and Johnson1976) showed that for a large aspect ratio circular cross-section plasma:
where the important factor
![]() $q^{2}-1$
removes, for
$q^{2}-1$
removes, for
![]() $q>1$
, the possibility of the instability predicted by Suydam (Reference Suydam1958) in a straight cylinder.) Thus we can write:
$q>1$
, the possibility of the instability predicted by Suydam (Reference Suydam1958) in a straight cylinder.) Thus we can write:
with the ‘effective’ curvature,
![]() $\unicode[STIX]{x1D705}_{\text{eff}}$
, deduced from (2.34). However, Hegna & Callen (Reference Hegna and Callen1994), perhaps seeking a
$\unicode[STIX]{x1D705}_{\text{eff}}$
, deduced from (2.34). However, Hegna & Callen (Reference Hegna and Callen1994), perhaps seeking a
![]() $D$
consistent with this argument, assumed
$D$
consistent with this argument, assumed
![]() $\unicode[STIX]{x1D705}_{\text{eff}}$
was the surface-averaged normal curvature,
$\unicode[STIX]{x1D705}_{\text{eff}}$
was the surface-averaged normal curvature,
![]() $\unicode[STIX]{x1D705}_{n}$
, and, furthermore, that
$\unicode[STIX]{x1D705}_{n}$
, and, furthermore, that
![]() $\unicode[STIX]{x1D705}_{n}\propto V^{\prime \prime }=(\text{d}\langle J\rangle /\text{d}\unicode[STIX]{x1D70C})$
, where
$\unicode[STIX]{x1D705}_{n}\propto V^{\prime \prime }=(\text{d}\langle J\rangle /\text{d}\unicode[STIX]{x1D70C})$
, where
![]() $\langle J\rangle =(\langle R^{2}\rangle q/R_{0}B_{0}g)$
, to obtain the following result for
$\langle J\rangle =(\langle R^{2}\rangle q/R_{0}B_{0}g)$
, to obtain the following result for
![]() $D$
:
$D$
:
However, at low
![]() $\unicode[STIX]{x1D6FD}$
and with
$\unicode[STIX]{x1D6FD}$
and with
![]() $B_{\unicode[STIX]{x1D719}}\simeq B$
(e.g. at large aspect ratio),
$B_{\unicode[STIX]{x1D719}}\simeq B$
(e.g. at large aspect ratio),
(Connor, Hastie & Helander Reference Connor, Hastie and Helander2009), so that their argument should have implied
Equation (2.39) is indeed consistent with our expression for
![]() $D$
in (2.21), and also with the work of Nishimura et al. (Reference Nishimura, Callen and Hegna1998) in the special case
$D$
in (2.21), and also with the work of Nishimura et al. (Reference Nishimura, Callen and Hegna1998) in the special case
![]() $g^{\prime }=0$
that they considered. Equations (2.21), (2.39) are not, however, consistent with
$g^{\prime }=0$
that they considered. Equations (2.21), (2.39) are not, however, consistent with
![]() $D=-(As^{2}/\unicode[STIX]{x1D70C}^{2})((1/4)+D_{M})$
, since
$D=-(As^{2}/\unicode[STIX]{x1D70C}^{2})((1/4)+D_{M})$
, since
![]() $\unicode[STIX]{x1D705}_{\text{eff}}\neq \unicode[STIX]{x1D705}_{n}$
.Footnote
4
We should not expect
$\unicode[STIX]{x1D705}_{\text{eff}}\neq \unicode[STIX]{x1D705}_{n}$
.Footnote
4
We should not expect
![]() $D$
to be exactly equal to
$D$
to be exactly equal to
![]() $-(As^{2}/\unicode[STIX]{x1D70C}^{2})((1/4)+D_{M})$
, because the ideal instability investigated by Mercier, and later by Greene & Johnson (Reference Greene and Johnson1962) using Hamada coordinates, is a mode with a range of coupled poloidal harmonics, whereas
$-(As^{2}/\unicode[STIX]{x1D70C}^{2})((1/4)+D_{M})$
, because the ideal instability investigated by Mercier, and later by Greene & Johnson (Reference Greene and Johnson1962) using Hamada coordinates, is a mode with a range of coupled poloidal harmonics, whereas
![]() $\unicode[STIX]{x1D713}$
of the envisaged tearing mode, has an isolated single poloidal harmonic.
$\unicode[STIX]{x1D713}$
of the envisaged tearing mode, has an isolated single poloidal harmonic.
It would be inconsistent with the ‘single poloidal harmonic’ assumption to simply replace
![]() $D(\unicode[STIX]{x1D70C})$
by the value corresponding to
$D(\unicode[STIX]{x1D70C})$
by the value corresponding to
![]() $D_{M}$
in (2.17); although the use of
$D_{M}$
in (2.17); although the use of
![]() $D_{M}$
would capture the poloidal mode coupling effects close to the singular surface that can have a profound effect on the Mercier indices, which in turn influence the value of the generalised
$D_{M}$
would capture the poloidal mode coupling effects close to the singular surface that can have a profound effect on the Mercier indices, which in turn influence the value of the generalised
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
stability parameter (Glasser et al.
Reference Glasser, Greene and Johnson1975).
$\unicode[STIX]{x1D6E5}^{\prime }$
stability parameter (Glasser et al.
Reference Glasser, Greene and Johnson1975).
3 Conclusions
Within the foregoing sections we have assumed that the perturbed poloidal flux function,
![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703})$
, contained only one poloidal harmonic,
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703})$
, contained only one poloidal harmonic,
![]() $\text{e}^{\text{i}m\unicode[STIX]{x1D703}}$
. However our solution for the variable
$\text{e}^{\text{i}m\unicode[STIX]{x1D703}}$
. However our solution for the variable
![]() $z$
, equation (2.10), contains a full spectrum of poloidal harmonics. Under these assumptions we have extended the validity of the tearing equation proposed by Hegna & Callen (Reference Hegna and Callen1994) to axisymmetric equilibria of arbitrary aspect ratio and arbitrary
$z$
, equation (2.10), contains a full spectrum of poloidal harmonics. Under these assumptions we have extended the validity of the tearing equation proposed by Hegna & Callen (Reference Hegna and Callen1994) to axisymmetric equilibria of arbitrary aspect ratio and arbitrary
![]() $\unicode[STIX]{x1D6FD}$
. In doing so we have only made use of the approximation,
$\unicode[STIX]{x1D6FD}$
. In doing so we have only made use of the approximation,
![]() $\unicode[STIX]{x1D716}^{2}/q_{s}^{2}\ll 1$
. This would certainly rule out the use of the resulting 1-D equation for studying internal kink type disruptions in tokamaks (where the
$\unicode[STIX]{x1D716}^{2}/q_{s}^{2}\ll 1$
. This would certainly rule out the use of the resulting 1-D equation for studying internal kink type disruptions in tokamaks (where the
![]() $m=n=1$
harmonic plays a crucial role), but should prove to be an accurate approximation for modes which are resonant in the pedestal region of a tokamak in H-mode. An unexpected result of this calculation has been the appearance of a new set of terms arising from the effect of the integration constant
$m=n=1$
harmonic plays a crucial role), but should prove to be an accurate approximation for modes which are resonant in the pedestal region of a tokamak in H-mode. An unexpected result of this calculation has been the appearance of a new set of terms arising from the effect of the integration constant
![]() $K$
(denoted by
$K$
(denoted by
![]() $\hat{A},~\hat{B},~{\hat{C}}$
and
$\hat{A},~\hat{B},~{\hat{C}}$
and
![]() $\hat{D}$
). However, it appears unlikely that such terms will play a significant role in determining tearing stability since they are normally negligibly small, except perhaps in very strongly shaped cross-sections or, e.g. in the vicinity of a separatrix boundary. For simplicity we ignored these extra terms in (2.17).
$\hat{D}$
). However, it appears unlikely that such terms will play a significant role in determining tearing stability since they are normally negligibly small, except perhaps in very strongly shaped cross-sections or, e.g. in the vicinity of a separatrix boundary. For simplicity we ignored these extra terms in (2.17).
It is also clear from the foregoing derivation of a 1-D equation that the pressure gradient term,
![]() $D(\unicode[STIX]{x1D70C})$
of (2.17), differs from the quantity
$D(\unicode[STIX]{x1D70C})$
of (2.17), differs from the quantity
![]() $-(As^{2}/\unicode[STIX]{x1D70C}^{2})((1/4)+D_{M})$
that would be expected in general tearing mode theory, as the singular surface is approached. The difference arises because the derivation of (2.17) is based on a single poloidal harmonic assumption, whereas retention of the coupled poloidal harmonics is required to capture the true value in the limit as
$-(As^{2}/\unicode[STIX]{x1D70C}^{2})((1/4)+D_{M})$
that would be expected in general tearing mode theory, as the singular surface is approached. The difference arises because the derivation of (2.17) is based on a single poloidal harmonic assumption, whereas retention of the coupled poloidal harmonics is required to capture the true value in the limit as
![]() $\unicode[STIX]{x1D70C}\rightarrow \unicode[STIX]{x1D70C}_{s}$
. The approach outlined in Fitzpatrick et al. (Reference Fitzpatrick, Hastie, Martin and Roach1993) retains seven coupled poloidal harmonics, but its restrictions to weak shaping and low
$\unicode[STIX]{x1D70C}\rightarrow \unicode[STIX]{x1D70C}_{s}$
. The approach outlined in Fitzpatrick et al. (Reference Fitzpatrick, Hastie, Martin and Roach1993) retains seven coupled poloidal harmonics, but its restrictions to weak shaping and low
![]() $\unicode[STIX]{x1D6FD}$
severely impede its application to the pedestal. The single poloidal harmonic approach outlined in this paper accommodates strong shaping and
$\unicode[STIX]{x1D6FD}$
severely impede its application to the pedestal. The single poloidal harmonic approach outlined in this paper accommodates strong shaping and
![]() $\unicode[STIX]{x1D6FD}$
effects, but neglects poloidal mode coupling that is needed to describe
$\unicode[STIX]{x1D6FD}$
effects, but neglects poloidal mode coupling that is needed to describe
![]() $D_{M}$
at the resonance and that may be important more globally. Nevertheless, for
$D_{M}$
at the resonance and that may be important more globally. Nevertheless, for
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
calculations at the foot of the pedestal where
$\unicode[STIX]{x1D6E5}^{\prime }$
calculations at the foot of the pedestal where
![]() $s^{2}$
becomes large near a separatrix boundary, both the exact Mercier indices and the approximate (1-D) ones return to similar, low
$s^{2}$
becomes large near a separatrix boundary, both the exact Mercier indices and the approximate (1-D) ones return to similar, low
![]() $\unicode[STIX]{x1D6FD}$
, values (of 0 and 1), and the 1-D approximation may give a good indication of tearing instability in a rather simple manner.
$\unicode[STIX]{x1D6FD}$
, values (of 0 and 1), and the 1-D approximation may give a good indication of tearing instability in a rather simple manner.
Numerical investigations of H-mode equilibria are presently underway.
Acknowledgements
This work has been carried out under the RCUK Energy Programme (grant number EP/P012450/1) with partial funding through the framework of the EUROfusion Consortium from the Euratom research and training programme 2014-2018 under grant agreement no. 633053. To obtain further information on the data and models underlying this paper please contact Email address for correspondence: PublicationsManager@ukaea.uk. The views and opinions expressed herein do not necessarily reflect those of the European Commission. The authors are grateful to C. Ham for helpful discussions.
Appendix A
We can generate unique expressions for the coefficients
![]() $B,~C$
and
$B,~C$
and
![]() $D$
, by exploiting the fact that all toroidal mode number dependencies in the 1-D tearing (2.17) can be expressed as powers, up to quadratic, of
$D$
, by exploiting the fact that all toroidal mode number dependencies in the 1-D tearing (2.17) can be expressed as powers, up to quadratic, of
![]() $m/(m-nq)$
.
$m/(m-nq)$
.
First, we collect all three terms in (2.16), that include parts proportional to
![]() $(m/(m-nq))^{2}$
and contribute to the coefficient
$(m/(m-nq))^{2}$
and contribute to the coefficient
![]() $D(\unicode[STIX]{x1D70C})$
in (2.17), namely;
$D(\unicode[STIX]{x1D70C})$
in (2.17), namely;
Now replacing
![]() $n$
by the identity
$n$
by the identity
![]() $(nq-m+m)/q$
and using
$(nq-m+m)/q$
and using
![]() $s=\unicode[STIX]{x1D70C}q^{\prime }/q$
, this expression becomes
$s=\unicode[STIX]{x1D70C}q^{\prime }/q$
, this expression becomes
where the first three terms yield (2.21) for
![]() $D$
and the last term now contributes to the expression for the coefficient
$D$
and the last term now contributes to the expression for the coefficient
![]() $C$
, rather than
$C$
, rather than
![]() $D$
. Three different terms from (2.16) and the final term of equation (A 2), contribute the term in (2.17) that is proportional to
$D$
. Three different terms from (2.16) and the final term of equation (A 2), contribute the term in (2.17) that is proportional to
![]() $m/(m-nq)$
, with the following factor in the coefficient:
$m/(m-nq)$
, with the following factor in the coefficient:
where the last term is the contribution from equation (A 2) above. Using (2.5), (2.6) and (2.8) for
![]() $T$
,
$T$
,
![]() $U$
and
$U$
and
![]() $W$
, the expression in (A 3) becomes:
$W$
, the expression in (A 3) becomes:
Now, on replacing
![]() $m$
by the identity
$m$
by the identity
![]() $m-nq+nq$
, we obtain the following expression:
$m-nq+nq$
, we obtain the following expression:
where the first two terms coincide with (2.20) for
![]() $C(\unicode[STIX]{x1D70C})$
, and the third term contributes to the coefficient
$C(\unicode[STIX]{x1D70C})$
, and the third term contributes to the coefficient
![]() $B(\unicode[STIX]{x1D70C})$
and exactly cancels the remaining
$B(\unicode[STIX]{x1D70C})$
and exactly cancels the remaining
![]() $n$
dependence in
$n$
dependence in
![]() $B$
, leading to (2.19) for
$B$
, leading to (2.19) for
![]() $B(\unicode[STIX]{x1D70C})$
.
$B(\unicode[STIX]{x1D70C})$
.
To demonstrate the second equality in (2.19) we consider cylindrical toroidal coordinates
![]() $R,Z,\unicode[STIX]{x1D719}$
. The Jacobian for the transformation
$R,Z,\unicode[STIX]{x1D719}$
. The Jacobian for the transformation
![]() $(R,Z)\rightarrow (\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703})$
is:
$(R,Z)\rightarrow (\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703})$
is:
We can obtain
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$
, using
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$
, using
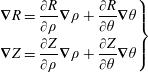 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D735}R=\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}+\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\\ \displaystyle \unicode[STIX]{x1D735}Z=\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}+\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D735}R=\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}+\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\\ \displaystyle \unicode[STIX]{x1D735}Z=\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}+\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\end{array}\right\} & & \displaystyle\end{eqnarray}$$
and deduce:
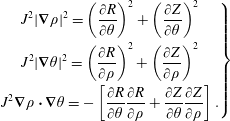 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle J^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}=\left(\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)^{2}\\ \displaystyle J^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}|^{2}=\left(\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\right)^{2}\\ \displaystyle J^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}=-\left[\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}+\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\right].\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle J^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|^{2}=\left(\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)^{2}\\ \displaystyle J^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}|^{2}=\left(\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\right)^{2}\\ \displaystyle J^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}=-\left[\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}+\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}Z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\right].\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Squaring and adding (A 6) and (A 7) using (A 8) one finds:
Appendix B
The 1-D tearing (2.17) is expressed in terms of equilibrium variables
![]() $\unicode[STIX]{x1D70C},g$
and
$\unicode[STIX]{x1D70C},g$
and
![]() $f$
. More familiar variables are the equilibrium poloidal flux
$f$
. More familiar variables are the equilibrium poloidal flux
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $I(\unicode[STIX]{x1D713})$
as used by Hegna & Callen (Reference Hegna and Callen1994). These are related by (2.27)–(2.29). In this appendix we give the form that (2.17) takes when expressed in these Hegna–Callen variables. Of the four terms in (2.17) we find:
$I(\unicode[STIX]{x1D713})$
as used by Hegna & Callen (Reference Hegna and Callen1994). These are related by (2.27)–(2.29). In this appendix we give the form that (2.17) takes when expressed in these Hegna–Callen variables. Of the four terms in (2.17) we find:
where, as in the work of Hegna and Callen, the dependent variable
![]() $\tilde{A}$
is the, single poloidal harmonic, tearing mode eigenfunction and
$\tilde{A}$
is the, single poloidal harmonic, tearing mode eigenfunction and
![]() $^{\prime }$
denotes the radial derivative with respect to
$^{\prime }$
denotes the radial derivative with respect to
![]() $\unicode[STIX]{x1D713}$
. Finally, on multiplying through by the factor
$\unicode[STIX]{x1D713}$
. Finally, on multiplying through by the factor
![]() $q/\unicode[STIX]{x1D70C}I$
we obtain the 1-D tearing equation in a rather simple form:
$q/\unicode[STIX]{x1D70C}I$
we obtain the 1-D tearing equation in a rather simple form:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D713}}\left[\frac{q}{I}\langle |\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}\rangle \frac{\text{d}\tilde{A}}{\text{d}\unicode[STIX]{x1D713}}\right]-\left\{\frac{m^{2}q}{I}\langle |\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}|^{2}\rangle -\frac{mq}{(m-nq)}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D713}}\left[I^{\prime }+\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{I}\langle R^{2}\rangle \right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,\frac{m^{2}q\unicode[STIX]{x1D707}_{0}p^{\prime }}{(m-nq)^{2}}\left[\frac{\text{d}}{\text{d}\unicode[STIX]{x1D713}}\left\langle \frac{R^{2}}{I}\right\rangle \right]\right\}\tilde{A}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D713}}\left[\frac{q}{I}\langle |\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}\rangle \frac{\text{d}\tilde{A}}{\text{d}\unicode[STIX]{x1D713}}\right]-\left\{\frac{m^{2}q}{I}\langle |\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}|^{2}\rangle -\frac{mq}{(m-nq)}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D713}}\left[I^{\prime }+\frac{\unicode[STIX]{x1D707}_{0}p^{\prime }}{I}\langle R^{2}\rangle \right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,\frac{m^{2}q\unicode[STIX]{x1D707}_{0}p^{\prime }}{(m-nq)^{2}}\left[\frac{\text{d}}{\text{d}\unicode[STIX]{x1D713}}\left\langle \frac{R^{2}}{I}\right\rangle \right]\right\}\tilde{A}=0.\end{eqnarray}$$


