Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T13:15:18.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady MHD flows with an ignorable co-ordinate and the potential transonic flow equation

Published online by Cambridge University Press:  13 March 2009

G. M. Webb ,
M. Brio  and
G. P. Zank
G. M. Webb
Affiliation:
Department of Planetary Sciences, University of Arizona, Tucson, Arizona 85721, U.S.A.
M. Brio
Affiliation:
Department of Mathematics, University fo Arizona, Tucson, Arizona 85721, U.S.A.
G. P. Zank
Affiliation:
Bartol Research Institute, The University of Delaware, Newark, Delaware 19716, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper explores the interrelationship between the generalized Grad-Shafranov equation, or trans-field force balance equation, for steady MHD flows with an ingnorable co-ordinate, and work by Imai on field-aligned MHD flows. The development of Imai, assumes at the outset that the fluid velocity V is parallel to the magnetic field B, and exploits an analogy with steady compressible irrotational flow in ordinary fluid dynamics. In Imai's analysis the magnetic induction B is written in the form B = σb, where 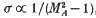, and MA is the appropriate Alfvén Mach number. Gauss' law Δ. B = Δ. (σb) = 0 then plays a role analogous to the mass continuity equation in ordinary fluid dynamics, where σ corresponds to the density of the pseudo-fluid. Imai's analysis leads to a transonic equation for the field potential φ defined by b = Δφ. For a restricted class of flows the trans-field force balance equation formulation also leads to the transonic potential flow equation, but the assumption of an ignorable co-ordinate allows for the possibility of non-field-aligned flows with non-zero electric field potential ΦE The characteristics of the generalized Grad—Shafranov equation are related to the Mach cone and the group velocity surface for linear magnetosonic waves. The corresponding forms of the characteristics for the potential transonic flow equation in the (x, y) plane and in the (bx, by) hodograph plane are discussed. Sample solutions of the potential transonic flow equation for radial, helical and spiral flows are obtained by means of the hodograph transformation, and are used to illustrate the differences between hyperbolic and elliptic flows. The potential transonic flow equation is obtained for the case of an ignorable co-ordinate z of a rectangular Cartesian co-ordinate system (x, y, z), and also for the case of flows with an ignorable co-ordinate of a spherical polar co-ordinate system (r, θ, ω). Astrophysical applications are briefly discussed.

Type
Research Article
Information
Journal of Plasma Physics , Volume 52 , Issue 1 , August 1994 , pp. 141 - 188
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Camenzind, M. 1986 Astron. Astrophys. 156, 137.Google Scholar
Camenzind, M. 1987 Astron. Astrophys. 184, 341.Google Scholar
Courant, R. & Friedrichs, K. O. 1948 Supersonic Flow and Shock Waves. Springer.Google Scholar
DeVille, A. & Priest, E. R. 1991 Geophys. Astrophys. Fluid Dyn. 61, 225.CrossRefGoogle Scholar
Heinemann, M. & Olbert, S. 1978 J. Geophys. Res. 83, 2457.Google Scholar
Heyvaerts, J. & Norman, C. A. 1989 Astrophys. J. 347, 1055.CrossRefGoogle Scholar
Hu, Y. Q. & Low, B. C. 1989 Astrophys. J. 342, 1049.Google Scholar
Imai, I. 1960 Rev. Mod. Phys. 32, 992.CrossRefGoogle Scholar
Jeffrey, A. & Taniuti, T. 1964 Non Linear Wave Propagation with Application to Physics and Magnetohydrodynamics. Academic.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn.Pergamon.Google Scholar
Lighthill, M. J. 1960 Phil. Trans. R. Soc. Lond. A 252, 397.Google Scholar
McKenzie, J. F. 1991 J. Geophys. Res. 96, 9491.CrossRefGoogle Scholar
Polovin, R. V. & Demutskii, V. P. 1990 Fundamentals of Magnetohydrodynamics. Consultants Bureau (Plenum).Google Scholar
Rutkevich, I. M. & Mond, M. 1992 J. Plasma Phys. 48, 345.CrossRefGoogle Scholar
Sakurai, T. 1985 Astron. Astrophys. 151, 121.Google Scholar
Sakurai, T. 1990 Comp. Phys. Rep. 12, 247.CrossRefGoogle Scholar
Sears, W. R. 1960 Rev. Mod. Phys. 32, 701.CrossRefGoogle Scholar
Seebass, R. 1961 Q. Appl. Maths 19, 231.Google Scholar
Sneddon, I. N. 1957 Elements of Partial Differential Equations. McGraw-Hill.Google Scholar
Sonnerup, B. U. Ö & Hau, L. N. 1994 J. Geophys. Res. 99, 143.Google Scholar
Spreiter, J. R. & Rizzi, A. W. 1974 Acta Astronautica 1, 15.Google Scholar
Spreiter, J. R., Summers, A. L. & Alksne, A. Y. 1966 Planet. Space Sci. 14, 223.CrossRefGoogle Scholar
Spreiter, J. R., Summers, A. L. & Rizzi, A. W. 1970 Planet. Space Sci. 18, 1281.CrossRefGoogle Scholar
Tsinganos, K. C. 1981 Astrophys. J. 245, 764.Google Scholar
Von Mises, R. 1958 Mathematical Theory of Compressible Fluid Flow. Academic.Google Scholar
Webb, G. M., Woodward, T. I., Brio, M. & Zank, G. P. 1993 J. Plasma Phys. 49, 465.CrossRefGoogle Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar