Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-18T01:02:02.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Axiomatizing Kripke's theory of truth

Published online by Cambridge University Press:  12 March 2014

Volker Halbach  and
Leon Horsten
Volker Halbach
Affiliation:
New College, Oxford OX 1 3BN, United Kingdom. E-mail: volker.halbach@philosophy.ox.ac.uk
Leon Horsten
Affiliation:
University of Leuven, Institute of Philosophy, Kardinaal Mercierplein 2, B-3000 Leuven, Belgium. E-mail: Leon.Horsten@hiw.kuleuven.be
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate axiomatizations of Kripke's theory of truth based on the Strong Kleene evaluation scheme for treating sentences lacking a truth value. Feferman's axiomatization KF formulated in classical logic is an indirect approach, because it is not sound with respect to Kripke's semantics in the straightforward sense: only the sentences that can be proved to be true in KF are valid in Kripke's partial models. Reinhardt proposed to focus just on the sentences that can be proved to be true in KF and conjectured that the detour through classical logic in KF is dispensable. We refute Reinhardt's Conjecture, and provide a direct axiomatization PKF of Kripke's theory in partial logic. We argue that any natural axiomatization of Kripke's theory in Strong Kleene logic has the same proof-theoretic strength as PKF. 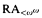namely the strength of the system ramified analysis or a system of Tarskian ramified truth up to ωω. Thus any such axiomatization is much weaker than Feferman's axiomatization KF in classical logic, which is equivalent to the system 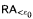of ramified analysis up to ε0.

Keywords

TruthKripke-Feferman theoryaxiomatic theories of truthreflective closureStrong Kleene schemepartial logicliar paradox
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 71 , Issue 2 , June 2006 , pp. 677 - 712
Copyright
Copyright © Association for Symbolic Logic 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aoyama, Hiroshi, The strong completeness of a system based on Kleene's strong three-valued logic, Notre Dame Journal of Formal Logic, vol. 35 (1994), pp. 355–368.CrossRefGoogle Scholar
[2]Beall, Jc and Armour-Garb, Brad. Deflationism and paradox, Clarendon Press, Oxford, 2005.CrossRefGoogle Scholar
[3]Belnap, Nuel and Gupta, Anil, The revision theory of truth, MIT Press, Cambridge, 1993.Google Scholar
[4]Blamey, Stephen, Partial logic, Handbook of philosophical logic (Gabbay, Dov M. and Guenthner, Franz, editors), vol. 5. Kluwer. Dordrecht, second ed., 2002, pp. 261–353.CrossRefGoogle Scholar
[5]Cantini, Andrea, Notes on formal theories of truth, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 35 (1989), pp. 97–130.CrossRefGoogle Scholar
[6]Cantini, Andrea, A theory of formal truth arithmetically equivalent to ID1. this Journal, vol. 55 (1990), pp. 244–259.Google Scholar
[7]Cantini, Andrea, Logical frameworks for truth and abstraction. An axiomatic study, Studies in Logic and the Foundations of Mathematics, vol. 135, Elsevier, Amsterdam, 1996.Google Scholar
[8]Cleave, John, The notion of logical consequence in the logic of inexact predicates, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 20 (1974), pp. 307–324.CrossRefGoogle Scholar
[9]Craig, William, Replacement of auxiliary expressions, Philosophical Review, vol. 65 (1956). pp. 38–55.Google Scholar
[10]Feferman, Solomon. Transfinite recursive progressions of axiomatic theories, this Journal, vol. 27 (1962), pp. 259–316.Google Scholar
[11]Feferman, Solomon, Systems of predicative analysis, this Journal, vol. 29 (1964), pp. 1–30.Google Scholar
[12]Feferman, Solomon, Reflecting on incompleteness, this Journal, vol. 56 (1991), pp. 1–49.Google Scholar
[13]Friedman, Harvey and Sheard, Michael, An axiomatic approach to self-referential truth, Annals of Pure and Applied Logic, vol. 33 (1987), pp. 1–21.CrossRefGoogle Scholar
[14]Friedman, Harvey and Sheard, Michael, The disjunction and existence properties for axiomatic systems of truth, Annals of Pure and Applied Logic, vol. 40 (1988), pp. 1–10.CrossRefGoogle Scholar
[15]Glanzbero, Michael. Minimalism, deflationism, and paradoxes. in [2, 107–132], 2005.CrossRefGoogle Scholar
[16]Halbach, Volker, A system of complete and consistent truth. Notre Dame Journal of Formal Logic, vol. 35 (1994), pp. 311–327.CrossRefGoogle Scholar
[17]Halbach, Volker, Axiomatische Wahrheitstheorien, Akademie Verlag, Berlin, 1996.CrossRefGoogle Scholar
[18]Halbach, Volker, Truth and reduction, Erkenntnis, vol. 53 (2000), pp. 97–126.CrossRefGoogle Scholar
[19]Halbach, Volker, Axiomatic theories of truth, Stanford Encyclopedia of Philosophy (Zalta, Edward N., editor), Spring 2006. forthcoming, http://plato.stanford.edu/archives/spr2006/entries/truth-axiomatic/.Google Scholar
[20]Halbach, Volker and Horsten, Leon, The deflationist's axioms for truth, in [2, 203–217], 2005.CrossRefGoogle Scholar
[21]Hempel, Carl, The theoretician's dilemma, Minnesota studies in the philosophy of science, II (Feigl, Herbertet al., editor). University of Minnesota press, 1958, pp. 37–98.Google Scholar
[22]Kearns, John, The strong completeness of a system for Kleene's three-valued logic, Zeitschrift für mathematische Logik und Grundlagen der Mathematik. vol. 25 (1979), pp. 61–68.CrossRefGoogle Scholar
[23]Kremer, Michael, Kripke and the logic of truth, Journal of Philosophical Logic, vol. 17 (1988), pp. 225–278.CrossRefGoogle Scholar
[24]Kripke, Saul, Outline of a theory of truth, Journal of Philosophy, vol. 72 (1975), pp. 690–712. reprinted in [25].CrossRefGoogle Scholar
[25]Martin, Robert L. (editor), Recent essays on truth and the Liar paradox, Clarendon Press and Oxford University Press, Oxford and New York, 1984.Google Scholar
[26]Martin, Robert L. and Woodruff, Peter W., On representing ‘true-in-L’ in L, Philosophia, vol. 5 (1975), pp. 213–217. Reprinted in [25].CrossRefGoogle Scholar
[27]Maudlin, Tim. Truth and paradox, Solving the riddles, Clarendon Press, Oxford. 2004.CrossRefGoogle Scholar
[28]McGee, Vann, Truth, vagueness, and paradox: An essay on the logic of truth, Hackett Publishing, Indianapolis and Cambridge, 1991.Google Scholar
[29]McGee, Vann, In praise of the free lunch: Why disquotationalists should embrace compositional semantics, manuscript. 2003.Google Scholar
[30]Montague, Richard, Syntactical treatments of modality, with corollaries on reflexion principles and finite axiomatizabilily, Acta Philosophica Fennica, vol. 16 (1963), pp. 153–67. Reprinted in [31, 286–302].Google Scholar
[31]Montague, Richard, Formal philosophy: Selected papers of Richard Montague, Yale University Press, New Haven and London, 1974. Edited and with an introduction by Richmond H. Thomason.Google Scholar
[32]Moschovakis, Yiannis N., Elementary induction on abstract structures, Studies in Logic and the Foundations of Mathematics, no. 77. North-Holland and Elsevier, Amsterdam, London and New York, 1974.Google Scholar
[33]Parsons, Charles, On n-quantifier induction, this Journal, vol. 37 (1972), pp. 466–482.Google Scholar
[34]Pohlers, Wolfram, Proof theory. An introduction, Springer, Berlin, 1989.Google Scholar
[35]Reinhardt, William, Remarks on significance and meaningful applicability, Mathematical logic and formal systems. A collection of papers in honor of Professor Newton C.A. Da Costa (de Alcantara, Luiz Paulo, editor), Lecture Notes in Pure and Applied Mathematics, vol. 94, Marcel Dekker inc., 1985, pp. 227–242.Google Scholar
[36]Reinhardt, William, Some remarks on extending and interpreting theories with a partial predicate for truth. Journal of Philosophical Logic, vol. 15 (1986), pp. 219–251.CrossRefGoogle Scholar
[37]Schwichtenberg, Helmut, Proof theory: Some applications of cut-elimination. Handbook of mathematical logic (Barwise, Jon. editor), Studies in Logic and the Foundations of Mathematics, no. 90. North-Holland, Amsterdam, London, New York and Tokyo, 1977, pp. 867–895.CrossRefGoogle Scholar
[38]Scott, Dana, Combinators and classes, λ-calculus and computer science (Böhm, Corrado. editor), Lecture Notes in Computer Science, Springer, Berlin, 1975, pp. 1–26.Google Scholar
[39]Sheard, Michael, Truth, probability, and naive criteria, Principles of truth (Halbach, Volker and Horsten, Leon, editors), Dr. Hänsel-Hohenhausen, Frankfurt a.M., 2002, pp. 169–181.Google Scholar
[40]Soames, Scott, Understanding truth, Oxford University Press, New York and Oxford, 1999.CrossRefGoogle Scholar
[41]Takeuti, Gaisi, Proof theory, second ed.. North Holland, Amsterdam, 1987.Google Scholar
[42]Troelstra, Anne S. and Schwichtenberg, Helmut, Basic proof theory. Cambridge Tracts in Theoretical Computer Science, no. 43, Cambridge University Press, Cambridge. 1997.Google Scholar
[43]Visser, Albert, Semantics and the liar paradox, Handbook of philosophical logic (Gabbay, Dov and Günthner, Franz, editors), vol. 4, Reidel, Dordrecht, 1989, pp. 617–706.CrossRefGoogle Scholar
[44]Wang, Hao, The calculus of partial predicates and its extension to set theory, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 7 (1961), pp. 283–288.CrossRefGoogle Scholar
[45]Woodruff, Peter W., On supervaluations in free logic, this Journal, vol. 49 (1984), pp. 943–950.Google Scholar