Analysability of finite U-rank types are explored both in general and in the theory 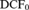${\rm{DC}}{{\rm{F}}_0}$. The well-known fact that the equation 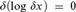$\delta \left( {{\rm{log}}\,\delta x} \right) = 0$ is analysable in but not almost internal to the constants is generalized to show that 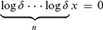$\underbrace {{\rm{log}}\,\delta \cdots {\rm{log}}\,\delta }_nx = 0$ is not analysable in the constants in 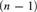$\left( {n - 1} \right)$-steps. The notion of a canonical analysis is introduced–-namely an analysis that is of minimal length and interalgebraic with every other analysis of that length. Not every analysable type admits a canonical analysis. Using properties of reductions and coreductions in theories with the canonical base property, it is constructed, for any sequence of positive integers 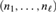$\left( {{n_1}, \ldots ,{n_\ell }} \right)$, a type in 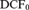${\rm{DC}}{{\rm{F}}_0}$ that admits a canonical analysis with the property that the ith step has U-rank 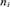${n_i}$.