Hostname: page-component-84b7d79bbc-g7rbq Total loading time: 0 Render date: 2024-07-30T13:22:53.093Z Has data issue: false hasContentIssue false
  • English
  • Français

ω-homomorphisms and ω-groups1

Published online by Cambridge University Press:  12 March 2014

C. H. Applebaum
C. H. Applebaum*
Affiliation:
Bowling Green State University, Bowling Green, Ohio
Get access Rights & Permissions [Opens in a new window]

Extract

Let ε stand for the set of nonnegative integers (numbers), V for the class of all subcollections of ε (sets), Λ for the set of isols, and 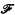for the set of mappings from a subset of ε into ε (functions). I f is a function we write δf and ρf for its domain and range respectively. The relation of inclusion is denoted by ⊂ and that of proper inclusion by ⊊. The sets α and β are recursively equivalent [written: α ≃ β], if δf = α and ρf = β for some function f with a one-to-one partial recursive extension f. We denote the recursive equivalence type of α, {σ ∈ V ∣ ≃ α}, by Req(α). Also R stands for Req(ε), while ΛR denotes the collection of all regressive isols. The reader is assumed to be familiar with the contents of [1] and [6].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 1 , March 1971 , pp. 55 - 65
Copyright
Copyright © Association for Symbolic Logic 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The results presented in this paper were taken from the author's doctoral dissertation written at Rutgers University under the direction of Professor J. C. E. Dekker.

References

[1]Applebaum, C. H. and Dekker, J. C. E., Partial recursive functions and ω-functions, this Journal (to appear).Google Scholar
[2]Dekker, J. C. E., Good choice sets, Annali della Scuola Normale Superiore di Pisa, Serie III, vol. 20 (1966), pp. 367–393.Google Scholar
[3]Dekker, J. C. E., Infinite series of isols, Proceedings of the Symposium on Recursive Function Theory, American Mathematical Society, Providence, Rhode Island, 1962, pp. 77–96.CrossRefGoogle Scholar
[4]Dekker, J. C. E., and Myhill, J., Recursive equivalence types, University of California Publications of Mathematics (N. S.), vol. 3 (1960), pp. 67–214.Google Scholar
[5]Hall, Marshall, The theory of groups, Macmillan, New York, 1959.Google Scholar
[6]Hassett, M. J., Recursive equivalence types and groups, this Journal, vol. 34 (1969), pp. 13–20.Google Scholar
[7]Nerode, A., Extension to isols, Annals of Mathematics, vol. 73 (1961), pp. 362–403.CrossRefGoogle Scholar
[8]Scott, W. R., Group theory, Prentice Hall, New Jersey, 1964.Google Scholar