Let k ⊂ K be a field extension, where K is an algebraically closed field of any characteristic and k is the prime field. Recall the following property of Hilbert Schemes (see, for example, [1], Proposition 1.16): Suppose 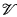⊂ 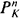× S is a flat family of closed subschemes of 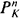parametrised by a scheme S/k. Then for every closed subscheme Z ⊂ 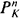in 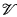, if [Z] denotes the Hilbert point of Z in Hilb(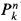) then the residue field of Hilb(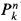) at [Z] is the minimal field of definition for Z. Intuitively, this says that as a family parametrised by Hilb(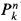), each fibre of 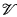lies above a point whose “co-ordinates” generate its minimal field of definition.

In the following note we are concerned with a more naive form of the above situation, for which we wish to give an elementary account. Suppose ϕ(x,y) is a system of polynomial equations over k (in variables x = (x1,…, xm) and parameters y = (y1, …, yn)), such that

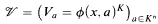
is a family of (possibly reducible) affine varieties in Km. Each nonempty member of this family has a unique minimal field of definition. The question arises as to whether it is possible to express this family of varieties using parameters that come, pointwise, from these minimal fields of definition. That is, is there a system of polynomial equations ψ(x, z) over k, such that each ψ(x, b) with b ∈ KN is of the form Va for some a ∈ Kn; and such that each Va ∈ 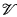is defined by ψ(x, b) for some b ∈ KN whose coordinates generate the minimal field of definition for Va? Moreover, we would like b to be obtained definably from a.