In this paper we shall construct nonregular ultrafilters showing many of the model-theoretic properties of their regular counterparts. The crucial idea in these constructions is to replace the use of regularity by independent functions. We shall use the notation and terminology of [1], our fundamental concepts being defined as follows:

Definition 1.1. (1) A uniform ultrafilter D over a cardinal κ is regular if there is a family {Xα ∣ α < κ} so that every infinite intersection of these Xα's is empty.

(2) A filter F over a cardinal κ is ω1-saturated if there is no family of sets {aα ∣ α < ω1} so that for every α < β < ω1

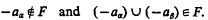
For more on regular ultrafilters, see [2]. The germinal theorem on the subject of nonregular ultrafilters is the following well-known result of Jack Silver:

Theorem 1.2 [1, Theorem 1.39]. If F is an ω1-saturated κ-complete filter over κ, then any ultrafilter extending F is nonregular.

This result will be the cornerstone of our constructions. Of course, the existence of a filter of the above type depends on large cardinal axioms. For more on un ω1-saturated κ-complete filters, see [1].