Consider any interpreted theory Θ, formulated in the notation of quantification theory (or lower predicate calculus) with interpreted predicate letters. It will be proved that Θ is translatable into a theory, likewise formulated in the notation of quantification theory, in which there is only one predicate letter, and it a dyadic one.

Let us assume a fragment of set theory, adequate to assure the existence, for all x and y without regard to logical type, of the set {x, y) whose members are x and y, and to assure the distinctness of x from {x, y} and {{x}}. ({x} is explained as {x, x}.) Let us construe the ordered pair x; y in Kuratowski's fashion, viz. as {{x}, {x, y}}, and then construe x;y;z as x;(y;z), and x;y;z;w as x;(y;z;w), and so on. Let us refer to w, w;w, w;w;w, etc. as 1w, 2w, 3w, etc.

Suppose the predicates of Θ are ‘F1’, ‘F2’, …, finite or infinite in number, and respectively d1-adic, d2-adic, …. Now let Θ′ be a theory whose notation consists of that of quantification theory with just the single dyadic predicate ‘F’, interpreted thus:

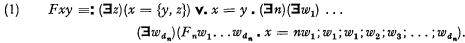
The universe of Θ′ is to comprise all objects of the universe of Θ and, in addition, {x, y) for every x and y in the universe of Θ′. (Of course the universe of Θ may happen already to comprise all this.)

Now I shall show how the familiar notations ‘x = y’, ‘x = {y, z}’, etc., and ultimately the desired ‘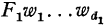’, ‘’, 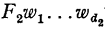etc. themselves can all be defined within Θ′.