The central notion of this paper is that of a κ-elementary end extension of a model of set theory. A model 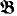is said to be a κ-elementary end extension of a model 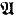of set theory if 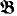> 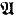and κ, which is a cardinal of 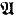, is end extended in the passage from 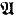to 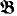, i.e., 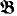enlarges κ without enlarging any of its members (see §0 for more detail). This notion was implicitly introduced by Scott in [Sco] and further studied by Keisler and Morley in [KM], Hutchinson in [H] and recently by the author in [E]. It is not hard to see that if 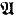has a κ-elementary end extension then κ must be regular in 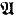. Keisler and Morley [KM] noticed that this has a converse if 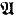is countable, i.e., if κ is a regular cardinal of a countable model 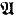then 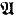has a κ-elementary end extension. Later Hutchinson [H] refined this result by constructing κ-elementary end extensions 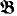1 and 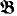2 of an arbitrary countable model 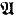in which κ is a regular uncountable cardinal, such that 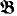1 adds a least new element to κ while 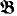2 adds no least new ordinal to κ. It is a folklore fact of model theory that the Keisler-Morley result gives soft and short proofs of countable compactness and abstract completeness (i.e. recursive enumera-bility of validities) of the logic L(Q), studied extensively in Keisler's [K2]; and Hutchinson's refinement does the same for stationary logic L(aa), studied by Barwise et al. in [BKM]. The proof of Keisler-Morley and that of Hutchinson make essential use of the countability of 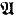since they both rely on the Henkin-Orey omitting types theorem. As pointed out in [E, Theorem 2.12], one can prove these theorems using “generic” ultrapowers just utilizing the assumption of countability of the 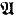-power set of κ. The following result, appearing as Theorem 2.14 in [E], links the notion of κ-elementary end extension to that of measurability of κ. The proof using (b) is due to Matti Rubin.