No CrossRef data available.
Published online by Cambridge University Press: 19 May 2023
We provide a complete classification, up to order-isomorphism, of all possible Wadge hierarchies on zero-dimensional Polish spaces using (essentially) countable ordinals as complete invariants. We also observe that although our assignment of invariants is very simple and there are only 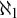 $ \aleph _1 $-many equivalence classes, the above classification problem is quite complex from the descriptive set-theoretic point of view: in particular, there is no Borel procedure to determine whether two zero-dimensional Polish spaces have isomorphic Wadge hierarchies. All results are based on a complete and explicit description of the Wadge hierarchy on an arbitrary zero-dimensional Polish space, depending on its topological properties.
$ \aleph _1 $-many equivalence classes, the above classification problem is quite complex from the descriptive set-theoretic point of view: in particular, there is no Borel procedure to determine whether two zero-dimensional Polish spaces have isomorphic Wadge hierarchies. All results are based on a complete and explicit description of the Wadge hierarchy on an arbitrary zero-dimensional Polish space, depending on its topological properties.