Greater economy can be effected in the primitive rules for the system K of basic logic by defining the existence operator ‘E’ in terms of two-place abstraction and the disjunction operator ‘V’. This amounts to defining ‘E’ in terms of ‘ε’, ‘έ’, ‘o, ‘ό’, ‘W’ and ‘V’, since the first five of these six operators are used for defining two-place abstraction.

We assume that the class Y of atomic U-expressions has only a single member ‘σ’. Similar methods can be used if Y had some other finite number of members, or even an infinite number of members provided that they are ordered into a sequence by a recursive relation represented in K. In order to define ‘E’ we begin by defining an operator ‘D’ such that

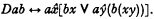
Here ‘a’ may be thought of as an existence operator that provides existence quantification over some finite class of entities denoted by a class A of U-expressions. In other words, suppose that ‘a’ is such that ‘ab’ is in K if and only if, for some ‘e’ in A, ‘be’ is in K. Then ‘Dab’ is in K if and only if, for some ‘e and ‘f’ in A, ‘be’ or ‘b(ef)’ is in K; and ‘a’, ‘Da’, ‘D(Da)’, and so on, can be regarded as existence operators that provide for existence quantification over successively wider and wider finite classes. In particular, if ‘a’ is ‘εσ’, then A would be the class Y having ‘σ’ as its only member, and we can define the unrestricted existence operator ‘E’ in such a way that ‘Eb’ is in K if and only if some one of ‘εσb’, ‘D(εσ)b’, ‘D(D(εσ))b’, and so on, is in K.