Article contents
A dichotomy theorem for turbulence
Published online by Cambridge University Press: 12 March 2014
Extract
In this note we show:
Theorem 1.1. Let G be a Polish group and X a Polish G-space with the induced orbit equivalence relation EG Borel as a subset of X × X. Then exactly one of the following:
(I) There is a countable languageℒand a Borel function
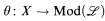
such that for all x1, x2 ∈ X
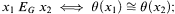
or
(II) there is a turbulent Polish G-space Y and a continuous G-embedding
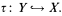
There are various bows and ribbons which can be woven into these statements. We can strengthen (I) by asking that θ also admit a Borel orbit inverse, that is to say some Borel function

for some Borel set B ⊂ Mod(ℒ), such that for all x ∈ X
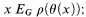
and then after having passed to this strengthened version of (I) we still obtain the exact same dichotomy theorem, and hence the conclusion that the two competing versions of (I) are equivalent. Similarly (II) can be relaxed to just asking that τ be a Borel G-embedding, or even simply a Borel reduction of the relevant orbit equivalence relations. It is in fact a consequence of 1.1 that all the plausible weakenings and strengthenings of (I) and (II) are respectively equivalent to one another.
I will not closely examine these possible variations here. The equivalences alluded to above follow from our main theorem and the results of [3]. That monograph had previously shown that (I) and (II) are incompatible, and proved a barbaric forerunner of 1.1, and gone on to conjecture the dichotomy result above.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002
References
REFERENCES
- 4
- Cited by




