Article contents
Ein Verfahren der mathematischen Logik
Published online by Cambridge University Press: 12 March 2014
Extract
Zu jedem Zählausdruck A in der allgemeinen pränexen Normalform
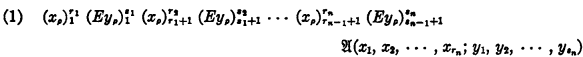
kann man bekanntlich einen, in bezug auf die Erfüllbarkeit, gleichwertigen Zählausdruck B in der spezielleren Normalform (Skolemsche Nonnalfonn)
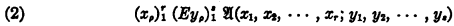
konstruieren, indem man auf A mehrmals (n–1 Mal) das sogenannte Skolemsche Verfahren anwendet. Dieses Verfahren hat nämlich die Eigenschaft, daß es auf einen Zählausdruck in der pränexen Normalform n-ten Grades (n > 1) angewandt zu einem gleichwertigen Zählausdruck in der pränexen Normalform (n–1)-ten Grades führt, wobei unter “Grad eines Zählausdrucks in der pränexen Normalform, die ein mit einem Allzeichen beginnendes und mit einem Seinszeichen endendes Präfix hat” die Anzahl der durch Seinszeichen voneinander getrennten Komplexe von Allzeichen dieses Präfixes zu verstehen ist. Da nun A—wie aus (1) ersichtlich ist—ein Zählausdruck n-ten Grades ist, so kommt man nach (n–1)-maliger Anwendung des Skolemschen Verfahrens tatsächlich zu einem gleichwertigen Zählausdruck ersten Grades, also zu einem gleichwertigen Zählausdruck der Form (2).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1938
References
1 Bei a ≦ b soll ![]() für (xα)(xα+1) … (xb) stehen und ähnlich
für (xα)(xα+1) … (xb) stehen und ähnlich ![]() für
für
Das Symbol ρ soll den variablen Index andeuten. Die Annahme, daß das voranstehende Quantorensystem (Präfix) mit einem Allzeichen beginnt und mit einem Seinszeichen endet, bildet offenbar keine wesentliche Einschränkung der allgemeinen pränexen Normalform.
2 Zwei Zählausdrücke mögen gleichwertig in bezug auf die Erfüllbarkeit oder kurz gleichwertig heißen, falls entweder beide erfüllbar oder beide nicht erfüllbar sind.
3 Vgl. Skolem, Th., Logisch-kombinatorische Untersuchungen über die Erfüllbarkeit oder Beweisbarkeil mathematischer Sätze usw., Skrifter utgit av Videnskapsselskapei i Kristiania, Math.-nat. Klasse 1920, Nr. 4., insb. S. 4–6Google Scholar. Vgl. auch Gödel, K., Die Vollständigkeit der Axiome des logischen Funktionenkalküls, Monatshefte für Mathematik und Physik, Bd. 37 (1930), S. 349–360, insb. S. 352–353CrossRefGoogle Scholar.
4 In demselben Sinn soll der Terminus “Grad eines Präfixes” verstanden werden.
5 Gödel, K., Zum Entscheidungsproblem des logischen Funktionenkalküls, Monatshefte für Mathematik und Physik, Bd. 40 (1933), S. 433–443, insb. S. 441CrossRefGoogle Scholar.
6 Diese Darstellbarkeit gilt, wie ich gezeigt habe (Pepis, J., Beiträge zur Reduktions-theorie des logischen Entscheidungsproblems, Acta scientiarum mathematicarum (Szeged), Bd. 8 (1936), S. 7–41, insb. Satz 8 und die Fußnoten 10 und 13)Google Scholar, übrigens auch in allen überabzählbaren Individuenbereichen.
7 Wird die Variable Xm in vm umbezeichnet, so kann man statt (4) kürzer
schreiben. Das Zeichen ∑ wird hier wie auch weiterhin als Konjunktionszeichen verwendet.
8 Falls A ein β-Ausdruck ist, so können diese zwei zweistelligen Funktionsvariablen mit den “ausgezeichneten” Funktionsvariablen R 1, R 2 von A identifiziert werden, so daß man dann überhaupt nur mit den n–1 einstelligen Funktionsvariablen auskommt (vgl. die in Fußnote 6 zitierte Arbeit).
9 Streng genommen, haben wir es demnach eigentlich mit zwei Modifikationen des Skolemschen Verfahrens zu tun: Eine ersetzt beim Skolemschen Verfahren die neue Funktionsvariable F(x 1, x 2, …, xm–1 vm) durch
und die andere durch
10 Durch Angabe des Verfahrens und den Beweis, daß es die angegebenen Eigenschaften hat, d. h. daß es zu gleichwertigen Zählausdrücken von den oben beschriebenen Formen führt, wird gleichzeitig eine Reihe von entsprechenden Reduktionssätzen des logischen Entscheidungsproblems der ersten Stufe mitbewiesen. U. a. ergibt sich so der Reduktionssatz der behauptet, daß man sich beim Erfüllbarkeitsproblem, ohne Beeinträchtigung der Allgemeinheit, auf Zählausdrücke der Form (5) beschränken darf. Es sei aber hervorgehoben, daß diese Reduktionssätze nur als Nebenresultate der vorliegenden Arbeit angesehen werden sollen, da ich in meiner Arbeit: Untersuchungen über das Enlscheidungs-problem der mathematischen Logik (erscheint wahrscheinlich in der Zeitschrift: Fundamenta mathematicae) durch kombinierte Anwendung einiger Methoden viel schärfere Reduktionssätze erziele als diese, welche aus der vorliegenden Arbeit unmittelbar zu ersehen sind. Z. B. wird dort gezeigt (Satz 35), daß das Erfüllbarkeitsproblem für Zählausdrücke der Form (5), welche außer Φ nur noch eine einzige, einstellige Funktionsvariable enthalten, bereits mit dem allgemeinen Entscheidungsproblem äquivalent ist.
11 Aus der Arbeit: Kalmár, L., Ein Beitrag zum Entsckeidungsproblem, Acta scientiarum mathemaiicarum (Szeged), Bd. 5 (1932), S. 222 236Google Scholar.
12 Der unserem Verfahren zugrunde liegende Gedanke ist eigentlich eine Zusammensetzung dreier Gedanken: eines Gedankens, W. Ackermann zu verdankenden(Beiträge zum Entscheidungsproblem der mathematischen Logik, Mathematische Annalen, Bd. 112 (1936), S. 419–432)Google Scholar, eines Gedankens aus meiner in der Fußnote 6 zitierten Arbeit und eines völlig neuen Gedankens.
13 D. h. Funktionen, deren Argumente und Werte Elemente von ![]() sind.
sind.
14 ![]() soll den durch Ersetzung der F 1, F 2, …, Fk durch die F′1, F′2, …, F′k aus
soll den durch Ersetzung der F 1, F 2, …, Fk durch die F′1, F′2, …, F′k aus ![]() entstehenden Ausdruck bezeichnen. Analoge Bedeutung sollen unten
entstehenden Ausdruck bezeichnen. Analoge Bedeutung sollen unten ![]() und
und ![]() haben.
haben.
15 Also eine zahlentheoretische Funktion.
16 Die Tai ersten Leerstellen sind der Reihe nach mit Ψi (x 1), x 2, x 3, … auszufüllen, was durchführbar ist, da einerseits die Funktion ![]() -stellig ist und da andrerseits Tai≦Tn, gilt. Im Falle rai <rn sollen die Tn, – rai übrigbleibenden Leerstellen durch x 1 ausgefüllt werden.
-stellig ist und da andrerseits Tai≦Tn, gilt. Im Falle rai <rn sollen die Tn, – rai übrigbleibenden Leerstellen durch x 1 ausgefüllt werden.
17 Man beachte, daß mit (32) gleichzeitig der Löwenheim-Skolemsche Satz mitbewiesen wurde. Unter der Annahme, daß der Zählausdruck A, der allgemeinen pränexen Normalform, in irgend einem Individuenbereich ![]() erfüllbar ist, wurde nämlich gezeigt, daß er dann auch im Bereich
erfüllbar ist, wurde nämlich gezeigt, daß er dann auch im Bereich ![]() der natürlichen Zahlen erfüllbar ist, und der Übergang von der allgemeinen pränexen Normalform zu Zählausdrücken ganz beliebiger Gestalt ist bekanntlich der leichteste Schritt beim Beweis des Löwenheim-Skolemschen Satzes. Natürlich ist in (32) eine noch viel schärfere Behauptung enthalten, von der wir bald Gebrauch machen. Wollte man nur einen Beweis für den Löwenheim-Skolemschen Satz haben, so würde sich der Beweis auf einige Zeilen reduzieren.
der natürlichen Zahlen erfüllbar ist, und der Übergang von der allgemeinen pränexen Normalform zu Zählausdrücken ganz beliebiger Gestalt ist bekanntlich der leichteste Schritt beim Beweis des Löwenheim-Skolemschen Satzes. Natürlich ist in (32) eine noch viel schärfere Behauptung enthalten, von der wir bald Gebrauch machen. Wollte man nur einen Beweis für den Löwenheim-Skolemschen Satz haben, so würde sich der Beweis auf einige Zeilen reduzieren.
18 C ist also der Zählausdruck, welcher aus B entsteht, indem man den Ausdruck R 1 (x, y) & R 2(x, z) für die Funktionsvariable Φ(x, y, z) einsetzt.
19 Dies folgt durch Kettenschluß aus folgenden zwei früher bewiesenen Tatsachen:
1. Ist B erfüllbar, so ist auch A erfüllbar.
2. Ist A erfüllbar, so hat B eine solche Erfüllung F 1*, F 1* …, F k*, Φ* im Bereich der natürlichen Zahlen ![]() . bei welcher Φ*(x, y, z) ≡ (x=Ψ1(y, z)) ≡ (x=2r−1(2z + 1)) ist.
. bei welcher Φ*(x, y, z) ≡ (x=Ψ1(y, z)) ≡ (x=2r−1(2z + 1)) ist.
20 Die Funktionen R 1*, R 2* können durch die Festsetzungen R 1*(x, y) ≡ (Eu)Φ*(x, y, u), R 2* (x, z) ≡ (Ev)Φ*(x, v, z) definiert werden.
21 Vgl. die in Fußnote 12 zitierte Arbeit.
22 F soll eine in A nicht vorkommende Funktionsvariable andeuten und Φ die in B 2 vorkommende dreistellige Funktionsvariable.
23 Da ja A, B als gleichwertige Zählausdrücke erkannt wurden.
24 Zum Beweis der Gleichwertigkeit der Zählausdrücke A, E genügt es, die Gleichwertigkeit der Zählausdrücke D, E nachzuweisen, und diese letztere beweist man in genau derselben Weise, in welcher wir die Gleichwertigkeit der Zählausdrücke B, C bewiesen haben.
25 Daraus ergibt sich auch sofort, daß man sich beim Erfüllbarkeitsproblem auf binäre Zählausdrücke der Ackermannschen Form (60) beschränken kann. In der in Fußnote 10 zitierten Arbeit beweise ich aber einen noch viel schärferen Reduktionssatz.
26 Man beachte, daß man in den bisherigen Arbeiten bei je einer Eliminierung einer n-stelligen mathematischen Funktionsvariablen Φ(x 1, x 2, …, xn), welche man dort nach dem Vorbilde der “beschreibenden” Funktionen von Russell und Whitehead (Principia mathematica, §13 und 14) ausführt, je eine neue (n+1)-stellige logische Funktionsvariable F(y, x 1, x 2, …, xn) (die der Beziehung y = Φ(x 1, x 2, …, xn) entspricht) heranzieht und dabei auch das =-Zeichen benutzt. Vgl. z. B. Herbrand, J., Sur le problème fondamental de la logique mathénatique, Sprawotdania Towarzystwa Nauhowego Warszawshiego, Wydz. III., Bd. 24 (1931), S. 12–66, insb. S. 33Google Scholar. Vgl. auch Gödel, K., Über formal unentschuldbare Sätze der Principia Mathematica und verwandter Systeme I, Monatshefte für Mathematik und Physik, Bd. 38 (1931), S. 173–198, insb. S. 194CrossRefGoogle Scholar.
- 15
- Cited by


