Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-01T15:00:42.529Z Has data issue: false hasContentIssue false
  • English
  • Français

FRACTAL DIMENSIONS OF k-AUTOMATIC SETS

Part of: Classical measure theory Computability and recursion theory

Published online by Cambridge University Press:  25 July 2023

ALEXI BLOCK GORMAN  and
CHRIS SCHULZ
ALEXI BLOCK GORMAN*
Affiliation:
DEPARTMENT OF MATHEMATICS THE OHIO STATE UNIVERSITY 231 W. 18TH AVE. COLUMBUS, OH 43210, USA
CHRIS SCHULZ
Affiliation:
PURE MATHEMATICS UNIVERSITY OF WATERLOO 200 UNIVERSITY AVENUE WEST WATERLOO, ON N2L 3G1 CANADA E-mail: c2schulz@uwaterloo.ca
*
E-mail: blockgorman.1@osu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper seeks to build on the extensive connections that have arisen between automata theory, combinatorics on words, fractal geometry, and model theory. Results in this paper establish a characterization for the behavior of the fractal geometry of “k-automatic” sets, subsets of 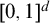$[0,1]^d$ that are recognized by Büchi automata. The primary tools for building this characterization include the entropy of a regular language and the digraph structure of an automaton. Via an analysis of the strongly connected components of such a structure, we give an algorithmic description of the box-counting dimension, Hausdorff dimension, and Hausdorff measure of the corresponding subset of the unit box. Applications to definability in model-theoretic expansions of the real additive group are laid out as well.

Keywords

Büchi automatafinite automatafractal geometryHausdorff dimensionHausdorff measurebox-counting dimensionentropymodel theorytame geometry

MSC classification

Primary: 03D05: Automata and formal grammars in connection with logical questions
Secondary: 28A80: Fractals
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 30
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamczewski, B. and Bell, J., An analogue of Cobham’s theorem for fractals . Transactions of the American Mathematical Society , vol. 363 (2011), pp. 4421–4442.CrossRefGoogle Scholar
Block Gorman, A., Pairs and predicates in expansions of o-minimal structures, Ph.D. thesis, University of Illinois at Urbana–Champaign, 2021.Google Scholar
Boigelot, B., Rassart, S., and Wolper, P., On the expressiveness of real and integer arithmetic automata (extended abstract) , Proceedings of the 25th International Colloquium on Automata, Languages and Programming , Springer, Berlin, Heidelberg, 1998, pp. 152–163.CrossRefGoogle Scholar
Büchi, J. R., On a decision method in restricted second order arithmetic , Proceedings of the International Congress on Logic, Method, and Philosophy of Science , Stanford University Press, Stanford, 1962, pp. 1–12.Google Scholar
Carton, O. and Michel, M., Unambiguous Büchi automata . Theoretical Computer Science , vol. 297 (2003), pp. 37–81.CrossRefGoogle Scholar
Charlier, E., Leroy, J., and Rigo, M., An analogue of Cobham’s theorem for graph directed iterated function systems . Advances in Mathematics , vol. 280 (2015), pp. 86–120.CrossRefGoogle Scholar
Chomsky, N. and Miller, G., Finite state languages . Information and Control , vol. 1 (1958), pp. 91–112.CrossRefGoogle Scholar
Edgar, G., Measure, Topology, and Fractal Geometry , second ed., Undergraduate Texts in Mathematics, Springer, New York, 2008.CrossRefGoogle Scholar
Evans, J., The entropy and Hausdorff dimension of self-similar sets . Proceedings of the American Mathematical Society , vol. 149 (2021), pp. 4387–4396.CrossRefGoogle Scholar
Falconer, K., Fractal geometry: Mathematical foundations and applications , Wiley, New York, 2013.Google Scholar
Hansel, G., Perrin, D., and Simon, I., Compression and entropy , Stacs 92 (Finkel, A. and Jantzen, M., editors), Springer, Berlin–Heidelberg, 1992, pp. 513–528.CrossRefGoogle Scholar
Hieronymi, P. and Walsberg, E., Interpreting the monadic second order theory of one successor in expansions of the real line . Israel Journal of Mathematics , vol. 224 (2018), pp. 39–55.CrossRefGoogle Scholar
Marker, D., Model Theory: An Introduction , Graduate Texts in Mathematics, Springer, New York, 2006.Google Scholar
Mauldin, R. D. and Williams, S. C., Hausdorff dimension in graph directed constructions . Transactions of the American Mathematical Society , vol. 309 (1988), pp. 811–829.CrossRefGoogle Scholar
McNaughton, R., Testing and generating infinite sequences by a finite automaton . Information and Control , vol. 9 (1966), no. 5, pp. 521–530.CrossRefGoogle Scholar
Merzenich, W. and Staiger, L., Fractals, dimension, and formal languages. RAIRO—Theoretical Informatics and Applications , 1993, vol. 28, pp. 361–386.CrossRefGoogle Scholar
Parker, A., Yancey, K., and Yancey, M., Regular language distance and entropy , 42nd International Symposium on Mathematical Foundations of Computer Science (MFCS 2017) (Larsen, K. G., Bodlaender, H. L., and Raskin, J.-F., editors), Leibniz International Proceedings in Informatics, Schloss Dagstuhl—Leibniz-Zentrum fuer Informatik, Dagstuhl, 2017, pp. 3:1–3:14.Google Scholar
Perrin, D. and Pin, J. É., Infinite Words: Automata, Semigroups, Logic and Games , Elsevier, Amsterdam, 2004.Google Scholar
Shannon, C. E., A mathematical theory of communication . The Bell System Technical Journal , vol. 27 (1948), no. 3, pp. 379–423.CrossRefGoogle Scholar
Staiger, L., The entropy of finite $\omega$ -languages . Problems of Control and Information Theory , vol. 14 (1985), no. 5, pp. 383–392.Google Scholar
Staiger, L., Combinatorial properties of the Hausdorff dimension . Journal of Statistical Planning and Inference , vol. 23 (1989), pp. 95–100.CrossRefGoogle Scholar