By Frege's Theorem is meant the result, implicit in Frege's Grundlagen, that, for any set E, if there exists a map υ from the power set of E to E satisfying the condition

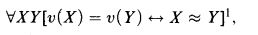
then E has a subset which is the domain of a model of Peano's axioms for the natural numbers. (This result is proved explicitly, using classical reasoning, in Section 3 of [1].) My purpose in this note is to strengthen this result in two directions: first, the premise will be weakened so as to require only that the map υ be defined on the family of (Kuratowski) finite subsets of the set E, and secondly, the argument will be constructive, i.e., will involve no use of the law of excluded middle. To be precise, we will prove, in constructive (or intuitionistic) set theory, the following

Theorem. Let υ be a map with domain a family of subsets of a set E to E satisfying the following conditions:

(i) ø ϵdom(υ)

(ii)∀U ϵdom(υ)∀x ϵ E − UU ∪ x ϵdom(υ)

(iii)∀UV ϵdom(5) υ(U) = υ(V) ⇔ U ≈ V.

Then we can define a subset N of E which is the domain of a model of Peano's axioms.