Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T23:53:40.996Z Has data issue: false hasContentIssue false
  • English
  • Français

Identities on cardinals less than ℵω

Published online by Cambridge University Press:  12 March 2014

M. Gilchrist  and
S. Shelah
M. Gilchrist
Affiliation:
Mathematics Department, Simon Fraser University, Burnaby, B. C., Canada, E-mail: gilchris@cs.sfu.ca
S. Shelah
Affiliation:
Institute of Mathematics, The Hebrew University, Jerusalem, Israel, E-mail: shelah@math.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Extract

Let κ be an uncountable cardinal and the edges of a complete graph with κ vertices be colored with ℵ0 colors. For 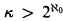the Erdős-Rado theorem implies that there is an infinite monochromatic subgraph. However, if 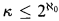, then it may be impossible to find a monochromatic triangle. This paper is concerned with the latter situation. We consider the types of colorings of finite subgraphs that must occur when the edges of the complete graph on 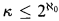vertices are colored with ℵ0 colors. In particular, we are concerned with the case ℵ1 ≤ κ ≤ ℵω.

The study of these color patterns (known as identities) has a history that involves the existence of compactness theorems for two cardinal models [2]. When the graph being colored has size ℵ1, the identities that must occur have been classified by Shelah [4]. If the graph has size greater than or equal to ℵω the identities have also been classified in [3]. The number of colors is fixed at ℵ0 as it is the natural place to start and the results here can be generalized to situations where more colors are used.

There is one difference that we now make explicit. When countably many colors are used we can define the following coloring of the complete graph on 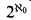vertices. First consider the branches in the complete binary tree of height ω to be vertices of a complete graph.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 61 , Issue 3 , September 1996 , pp. 780 - 787
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baumgartner, J. M., Almost-disjoint sets, Annals of Mathematical Logic, vol. 10 (1976), pp. 401–439.CrossRefGoogle Scholar
[2]Schmerl, J., Transfer theorems and their applications to logics, Model theoretic logics, 1985, pp. 177–209.Google Scholar
[3]Shelah, S., A two cardinal theorem and a combinatorial theorem, Proceedings of the American Mathematical Society, vol. 62 (1977), no. 1, pp. 134–136.CrossRefGoogle Scholar
[4]Shelah, S., Appendix to models with second order properties II, Annals of Mathematical Logic, vol. 14 (1978), pp. 223–226.CrossRefGoogle Scholar
[5]Shelah, S., Models with second order properties II, Annals of Mathematical Logic, vol. 14 (1978), pp. 73–87.CrossRefGoogle Scholar
[6]Shelah, S. and Stanley, L., A theorem and some consistency results in partition calculus, Annals of Pure and Applied Logic, vol. 36 (1987), pp. 119–152.CrossRefGoogle Scholar