We prove an effective version of the Lopez-Escobar theorem for continuous domains. Let $Mod(\tau )$ be the set of countable structures with universe 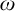$\omega $ in vocabulary $\tau $ topologized by the Scott topology. We show that an invariant set 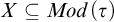$X\subseteq Mod(\tau )$ is 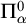$\Pi ^0_\alpha $ in the Borel hierarchy of this topology if and only if it is definable by a 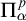$\Pi ^p_\alpha $-formula, a positive 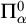$\Pi ^0_\alpha $ formula in the infinitary logic 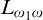$L_{\omega _1\omega }$. As a corollary of this result we obtain a new pullback theorem for positive computable embeddings: Let $\mathcal {K}$ be positively computably embeddable in 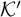$\mathcal {K}'$ by $\Phi $, then for every 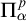$\Pi ^p_\alpha $ formula 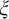$\xi $ in the vocabulary of 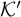$\mathcal {K}'$ there is a 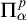$\Pi ^p_\alpha $ formula 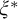$\xi ^{*}$ in the vocabulary of 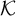$\mathcal {K}$ such that for all $\mathcal {A}\in \mathcal {K}$, 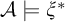$\mathcal {A}\models \xi ^{*}$ if and only if 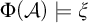$\Phi (\mathcal {A})\models \xi $. We use this to obtain new results on the possibility of positive computable embeddings into the class of linear orderings.