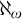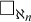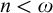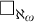1. Introduction and background
The properties of singulars of uncountable cofinality are notoriously different from those of countable cofinality. A prime example is Silver’s theorem that
${{\mathsf {GCH}}}$
cannot fail for the first time at a singular of uncountable cofinality. In contrast, Magidor showed that
${ {\mathsf {GCH}}}$
can fail for the first time at
$\aleph _\omega $
. There is therefore a natural question of whether this phenomenon generalizes to more complex structures.Footnote
1
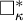
Here we focus on the combinatorial properties of inner models, notably square principles. Jensen originally distilled the principle
$\square _\kappa $
(where
$\kappa $
is some given cardinal) to study the properties of Gödel’s Constructible Universe L [Reference Jensen7]. Many variations of
$\square _\kappa $
have been studied since then. (Precise definitions will be given below, but Cummings, Foreman, and Magidor [Reference Cummings, Foreman and Magidor3] is the canonical reference for this area.) There is in general a tension between square principles and large cardinals, one instance of which is that
$\square _\kappa $
fails if
$\kappa $
is larger than a supercompact cardinal. Moreover, the failure of
$\square _\kappa $
at a singular cardinal
$\kappa $
requires considerable consistency strength from large cardinals [Reference Sargsyan13]. The models of interest in this area realize some compatibility of both square principles and the compactness properties exhibited by large cardinals.
In this paper we will address the compactness of square principles themselves: whether or not
$\square _\kappa $
necessarily holds for some cardinal
$\kappa $
if
$\square _\delta $
holds for sufficiently many cardinals
$\delta <\kappa $
. Cummings, Foreman, and Magidor proved that it is consistent that
$\square _{\aleph _n}$
holds for
$1 \le n < \omega $
but that
$\square _{\aleph _\omega }$
fails [Reference Cummings, Foreman and Magidor4]. Later, Krueger improved the result by obtaining a bad scale on
$\aleph _\omega $
in a similar model [Reference Krueger8]. But such results can also go in the other direction: Cummings, Foreman, and Magidor also proved that if
$\square _{\aleph _n}$
holds for all
$n<\omega $
, there is an object that to some extent resembles a
$\square _{\aleph _\omega }$
-sequence but with a weaker coherence property [Reference Cummings, Foreman and Magidor5]. The main result of this paper is along these lines.
Theorem 1.1. Suppose that
$\kappa $
is a singular strong limit of cofinality
$\lambda>\omega $
such that for some stationary set
$S \subseteq \kappa $
,
$\square _\delta ^*$
holds for all
$\delta \in S$
and
$\prod _{\delta \in S}\delta ^+$
carries a good scale. Then
$\square _\kappa ^*$
holds.
This represents some progress on a question raised by Golshani online regarding a supposed Silver’s Theorem for special Aronszajn trees [Reference Golshani6]: at any cardinal
$\delta $
,
$\square _\delta ^*$
is equivalent to the existence of a special
$\delta ^+$
-Aronszajn tree [Reference Cummings2].
The difference between the results of Cummings, Foreman, and Magidor and Theorem 1.1 is that the resulting sequence is fully coherent—not just coherent at points of uncountable cofinality. In other words, we are able to obtain some compactness for a canonical object by obtaining exactly that canonical object in the end. We nonetheless depend on the goodness of scales, as do Cummings, Foreman, and Magidor.
Note that the use of stationarity in Theorem 1.1 is important.
Proposition 1.2. Assuming the consistency of a supercompact cardinal, it is consistent that
$\square _{\aleph _\alpha }$
holds for all double successor ordinals
$\alpha <\omega _1$
and that there is a bad scale on
$\aleph _{\omega _1}$
, hence
$\square _{\aleph _{\omega _1}}$
fails.
Proof We work in
$V[{\text {Col}}(\aleph _1,<\! \kappa )],$
where
$\kappa $
is supercompact and assume
${ {\mathsf {GCH}}}$
holds in this model. Let
${\mathbb {S}}_\alpha $
be the standard forcing for adding
$\square _{\aleph _\alpha }$
. We force with a product
$\prod _{\alpha =\beta +2<\omega _1}{\mathbb {S}}_\alpha $
to get a model W in which
$\square _{\aleph _\alpha }$
holds for all double successor ordinals
$\alpha <\aleph _{\omega _1}$
. We will argue that this model has a bad scale carried by
$\aleph _{\omega _1}$
.
For double successor ordinals
$\alpha <\aleph _{\omega _1+1}$
, let
${\mathbb {T}}_\alpha $
be the poset threading the square sequence added by
${\mathbb {S}}_\alpha $
with a thread of length
$\aleph _\alpha $
. (We are using that
$\alpha $
is a successor and hence
$\aleph _\alpha $
is regular, hence
${\mathbb {T}}_\alpha $
is well-defined.) There is a natural complete embedding
$\iota : \prod _{\alpha =\beta +2<\omega _1}{\mathbb {S}}_\alpha \hookrightarrow {\mathbb {P}}:= \prod _{\alpha =\beta +2<\omega _1}{\mathbb {S}}_\alpha \ast {\mathbb {T}}_\alpha $
. If
$\gamma <\omega _1$
is a limit ordinal, then
${\mathbb {P}}^\gamma _{\text {low}}:= \prod _{\alpha =\beta +2<\gamma }{\mathbb {S}}_\alpha \ast {\mathbb {T}}_\alpha $
has cardinality
$\aleph _{\gamma +1}$
by
${ {\mathsf {GCH}}}$
while
${\mathbb {P}}_\gamma ^{\text {high}}:= \prod _{\gamma <\alpha =\beta +2<\omega _1}{\mathbb {S}}_\alpha \ast {\mathbb {T}}_\alpha $
is
$\aleph _{\gamma +2}$
-closed. Therefore
${\mathbb {P}}:={\mathbb {P}}^\gamma _{\text {low}} \times {\mathbb {P}}_\gamma ^{\text {high}}$
preserves
$\aleph _{\gamma +2}$
, and so we can see that
${\mathbb {P}}$
preserves
$\aleph _{\omega _1+1}$
(even though many cardinals are collapsed in between). Since
$\prod _{\alpha =\beta +1<\omega _1}{\mathbb {S}}_\alpha $
embeds into an
$\aleph _{\omega _1}$
-preserving forcing, it too is
$\aleph _{\omega _1}$
-preserving.
Standard lifting arguments then show that there is a bad scale on
$\aleph _{\omega _1}^W$
in the extension by the product of threads, but this implies that there is already a bad scale in W, and hence that
$\square _{\aleph _{\omega _1}}^*$
fails.
We also note that there exists in the literature a contrast to Theorem 1.1 in the case of
$\aleph _\omega $
, even with good scales.
Fact 1.3. It is consistent that
$\square _{\aleph _n}^*$
holds for all
$n<\omega $
, all scales are good, and
$\square _{\aleph _\omega }^*$
fails.
If
$\kappa _0 = \aleph _0$
and
${\langle {\kappa _n} : {1<n<\omega } \rangle }$
is a sequence of supercompact cardinals in some ground model, then Fact 1.3 is witnessed in an extension by
$\prod _{n<\omega }{\text {Col}}(\kappa _{n-1},<\kappa _n),$
where
$\kappa _{-1} = \aleph _1$
: Magidor and Shelah showed that all scales on
$\aleph _\omega $
are good in this model [Reference Magidor11],
$\square _{\aleph _\omega }^*$
fails because the strong reflection property holds (see Section 4 of [Reference Cummings, Foreman and Magidor3]), and
$\square _{\aleph _n}^*$
holds for all
$n<\omega $
because of
${ {\mathsf {GCH}}}$
by a theorem of Specker.
For the remainder of the introduction, we will focus on definitions. In Section 2 we will prove Theorem 1.1. At the end of the paper we will prove that a result similar to Theorem 1.1 holds for partial squares.
Theorem 1.4. Let
$\kappa $
be a singular strong limit cardinal of cofinality
$\lambda>\omega $
. Suppose there is a stationary set
$S \subset \kappa $
such that
$\square _\delta $
holds for all
$\delta \in S$
and such that
$\prod _{\delta \in S} \delta ^+$
carries a good scale. Then there is a partial square sequence on
$\kappa ^+ \cap \operatorname {\mathrm {cof}}(> \lambda )$
.
1.1. Definitions
We define square sequences in terms of a hierarchy introduced by Schimmerling [Reference Schimmerling14].
Definition 1.5. We say that
$\langle \mathcal {C}_\alpha \mid \alpha \in \lim (\kappa ^+)\rangle $
is a
$\square _{\kappa ,\lambda }$
-sequence if for all limit
$\alpha < \kappa ^+$
:
-
(1) each
$C\in \mathcal {C}_\alpha $
is a club subset of
$\alpha $
with
$\operatorname {\mathrm {ot}}(C)\leq \kappa $
; -
(2) for every
$C\in \mathcal {C}_\alpha $
, if
$\beta \in \lim (C)$
, then
$C\cap \beta \in \mathcal {C}_\beta $
; -
(3)
$1\leq |\mathcal {C}_\alpha |\leq \lambda $
.
The principle
$\square _{\kappa , 1}$
is the original
$\square _\kappa $
, and
$\square _{\kappa ,\kappa }$
is the weak square, denoted
$\square ^*_\kappa $
.
Definition 1.6. If
$\mu $
is a cardinal and
$S \subset \lim (\mu ^+)$
is stationary, then we say that
${\langle {C_\alpha } : {\alpha \in S} \rangle }$
is a partial square sequence if for all
$\alpha \in S$
:
-
(1)
$C_\alpha $
is closed and unbounded in
$\alpha $
; -
(2)
$\operatorname {\mathrm {ot}}(C_\alpha ) \le \mu $
; -
(3) if
$\beta \in S$
and
$\gamma \in \lim C_\alpha \cap \lim C_\beta $
, then
$C_\alpha \cap \gamma = C_\beta \cap \gamma $
.
Definition 1.7.
-
(1) If
$\tau $
is a cardinal and
$f,g : \tau \to {\text {ON}}$
, then
$f <^\ast g$
if there is some
$j<\tau $
such that
$f(i)<g(i)$
for all
$i \ge j$
. The analogous definitions hold for
$>^*$
and
$=^*$
. -
(2) Given a singular cardinal
$\kappa $
, we say that a strictly increasing sequence
$\vec \kappa = {\langle {\mu _i} : {i<\operatorname {\mathrm {cf}} \kappa } \rangle }$
of regular cardinals converging to
$\kappa $
is a product when we regard
$\prod _{i<\operatorname {\mathrm {cf}} \kappa }\mu _i$
as a space. -
(3) Given a product
$\vec \kappa = \prod _{i<\operatorname {\mathrm {cf}} \kappa } \mu _i$
, a sequence
${\langle {f_\alpha } : {\alpha <\kappa ^+} \rangle }$
is a scale on
$\vec \kappa $
if:-
(a) for all
$\alpha <\kappa ^+$
,
$f_\alpha \in \vec \kappa $
, i.e.,
$f_\alpha (i)<\mu _i$
for all
$i<\operatorname {\mathrm {cf}} \kappa $
; -
(b) for all
$\beta <\alpha <\kappa ^+$
,
$f_\alpha <^\ast f_\beta $
; -
(c) for all
$g \in \vec \kappa $
, there is some
$\alpha <\kappa ^+$
such that
$g<^\ast f_\alpha $
(i.e
$. {\langle {f_\alpha } : {\alpha <\kappa ^+} \rangle }$
is cofinal in the product
$\vec \kappa $
).
We also say that the product
$\vec \kappa $
carries
$\vec f$
. -
-
(4) We will use the term pseudo-scale for an object resembling a scale that is not necessarily cofinal in the product
$\vec \kappa $
, i.e
$.,$
it satisfies (a) and (b) of the previous item. (However, since pseudo-scales have exact upper bounds, they are cofinal in some product, see [Reference Abraham, Magidor, Foreman and Kanamori1].) -
(5) Given a scale (or pseudo-scale)
$\vec f = {\langle {f_\alpha } : {\alpha <\kappa ^+} \rangle }$
,
$\alpha < \kappa ^+$
is good if there is some unbounded
$A \subset \alpha $
with
$\operatorname {\mathrm {ot}} A = \operatorname {\mathrm {cf}} \alpha $
and some
$j<\operatorname {\mathrm {cf}} \kappa $
such that for all
$i \ge j$
,
${\langle {f_\beta (i)} : {\beta \in A} \rangle }$
is strictly increasing. -
(6) If there is a club
$D \subset \kappa ^+$
such that every
$\alpha \in D$
with
$\operatorname {\mathrm {cf}} \alpha> \operatorname {\mathrm {cf}} \kappa $
is a good point of
$\vec f$
, then
$\vec f$
is a good scale. An analogous definition applies for good pseudo-scales.
The reason for defining pseudo-scales is that the cofinality clause of the definition of a scale will be largely irrelevant for our purposes.
2.
${ {\mathsf {ZFC}}}$
results
In this section we will prove the main results of the paper. We clarify notions of continuity in Section 2.1, then we prove Theorem 1.1 in Section 2.2, and then we sketch an analogous theorem for partial squares in Section 2.3.
2.1. Continuity
Our goal in this section is to obtain a strong concept of the continuity used by Cummings, Foreman, and Magidor for scales on a singular cardinal
$\kappa $
of cofinality
$\lambda $
. The material concerning points
$\alpha $
such that
$\operatorname {\mathrm {cf}}(\alpha )>\lambda $
is the same as theirs, but we want to consider some issues that arise when
$\operatorname {\mathrm {cf}}(\alpha ) \le \lambda $
. Specifically, continuity is trivial if
$\operatorname {\mathrm {cf}}(\alpha )<\lambda $
, and we would like to modify the concept of continuity for the situation where
$\operatorname {\mathrm {cf}}(\alpha )=\lambda $
so that the square sequences we define are coherent.
Fix a singular
$\kappa $
of cofinality
$\lambda>\omega $
. We will consider some fixed stationary
$S \subseteq \lambda $
and a product
$\vec \kappa = \prod _{i \in S} \mu _i$
. This formulation will be important when we are considering
$\alpha \in \kappa ^+ \cap \operatorname {\mathrm {cof}}(\lambda )$
. Fix a pseudo-scale
$\vec f$
on
$\vec \kappa $
.
Proposition 2.1. If
$\operatorname {\mathrm {cf}} \alpha> \operatorname {\mathrm {cf}} \kappa $
and
$\alpha $
is a good point, then for any cofinal
$B \subset \alpha $
with
$\operatorname {\mathrm {ot}} B = \operatorname {\mathrm {cf}} \alpha $
, there is some
$B^\ast \subseteq B$
such that
$B^*$
witnesses goodness of
$\alpha $
.
This follows from what is known as “The Sandwich Argument.”
Proof Suppose
$A \subset \alpha $
witnesses goodness. Let
$\tau = \operatorname {\mathrm {cf}} \alpha $
and enumerate
$A' := {\langle {\alpha _\xi } : {\xi <\tau } \rangle } \subset A$
and
$B' := {\langle {\beta _\xi } : {\xi <\tau } \rangle } \subset B$
in such a way that for all
$\xi <\tau $
,
$f_{\alpha _\xi } \le ^* f_{\beta _\xi } <^* f_{\alpha _{\xi +1}}$
. Observe that
$A'$
also witnesses goodness of
$\alpha $
with respect to some
$j'$
. For each
$\xi <\tau $
, let
$j_\xi \ge j'$
be such that
$i \ge j_\xi $
implies
$f_{\alpha _\xi }(i) \le f_{\beta _\xi }(i) < f_{\alpha _{\xi +1}}(i)$
. Then there is some unbounded
$X \subset \tau $
and some
$j<\lambda $
such that for all
$\xi <\tau $
,
$j_\xi = j$
. Since j also witnesses goodness with respect to
$A'$
, this means that if
$\xi ,\eta \in X$
and
$\xi < \eta $
, then for all
$i \ge j$
, we have
$f_{\beta _\xi }(i) < f_{\alpha _{\xi +1}}(i) \le f_{\alpha _\eta }(i) \le f_{\beta _\eta }(i)$
. We have proved the proposition with
$B^* = {\langle {\beta _\xi } : {\xi \in X} \rangle }$
.
Modulo a short argument, this implies:
Proposition 2.2 (See Remark 11.1 in [Reference Cummings2]).
If a product
$\vec \kappa $
carries a good scale
$\vec f$
, then there is a scale
$\vec g$
such that every
$\alpha $
with
$\operatorname {\mathrm {cf}} \alpha> \operatorname {\mathrm {cf}} \kappa $
is a good point of
$\vec g$
.
Definition 2.3. Suppose
$\vec f = {\langle {f_\alpha } : {\beta <\alpha } \rangle }$
is a
$<^*$
-increasing sequence on the product
$\vec \kappa = \prod _{i \in S}\mu _i$
, and that
$A \subset \alpha $
is unbounded for some
$\alpha < \kappa ^+$
with
$\operatorname {\mathrm {ot}} A = \operatorname {\mathrm {cf}} \alpha $
.
-
•
$\vec f_A$
denotes the function
$i \mapsto \sup _{\beta \in A}f_\beta (i)$
; -
• if
$\operatorname {\mathrm {cf}} \alpha = \operatorname {\mathrm {cf}} \kappa $
and
$A = {\langle {\beta _i} : {i<\operatorname {\mathrm {cf}} \kappa } \rangle }$
,
$\vec f^\Delta _A$
denotes the function
$i \mapsto \sup _{j<i}f_{\beta _j}(i)$
.
Definition 2.4. If f and g are functions on a product
$\vec \kappa $
, we write
$f =^*_\Delta g$
if there is a club
$C \subseteq \lambda $
such that for all
$i \in C \cap S$
,
$f(i)=g(i)$
. The definition for
$f<^*_\Delta g$
is analogous.
Definition 2.5. A scale
$\vec f = {\langle {f_\alpha } : {\alpha <\kappa ^+} \rangle }$
is totally continuous if the following hold:
-
• if
$\operatorname {\mathrm {cf}} \alpha < \operatorname {\mathrm {cf}} \kappa $
, then for all cofinal
$A \subset \alpha $
with
$\operatorname {\mathrm {ot}} A = \operatorname {\mathrm {cf}} \alpha $
,
$(\vec f {\upharpoonright } \alpha )_A =^\ast f_\alpha $
; -
• if
$\operatorname {\mathrm {cf}} \alpha = \operatorname {\mathrm {cf}} \kappa $
, then for all clubs
$A \subset \alpha $
such that
$\operatorname {\mathrm {ot}} A = \operatorname {\mathrm {cf}} \alpha $
, we have
$f_\alpha =^*_\Delta (\vec f {\upharpoonright } \alpha )_A^\Delta $
; -
• if
$\operatorname {\mathrm {cf}} \alpha> \operatorname {\mathrm {cf}} \kappa $
, then
$\alpha $
is a good point,
$f_\alpha $
is an exact upper bound of
${\langle {f_\beta } : {\beta < \alpha } \rangle }$
, and for all cofinal
$A \subset \alpha $
witnessing goodness of
$\alpha $
, we have
$(\vec f {\upharpoonright } \alpha )_A =^* f_\alpha $
.
Even though these cases are different, we will say by continuity if we invoke any of them.
Now we work towards:
Lemma 2.6. If
$\operatorname {\mathrm {cf}} \kappa = \lambda> \omega $
,
$S \subset \lambda $
is stationary, and
$\vec \kappa = \prod _{i \in S} \mu _i$
is a product of regular cardinals on
$\kappa $
that carries a good scale, then it carries a totally continuous good scale.
Fix a
$<^*$
-increasing sequence
$\vec f = {\langle {f_\alpha } : {\beta <\alpha } \rangle }$
on a product
$\prod _{i<\operatorname {\mathrm {cf}} \kappa }\mu _i$
. The following is straightforward:
Proposition 2.7. Suppose
$\alpha <\kappa ^+$
,
$\operatorname {\mathrm {cf}} \alpha < \operatorname {\mathrm {cf}} \kappa $
,
$A,B \subset \alpha $
are unbounded and
$\operatorname {\mathrm {ot}} A =\operatorname {\mathrm {ot}} B = \operatorname {\mathrm {cf}} \alpha $
. Then
$\vec f_A =^\ast \vec f_B$
.
Proposition 2.8. If
$\operatorname {\mathrm {cf}} \alpha> \operatorname {\mathrm {cf}} \kappa $
and
$A \subset \alpha $
witnesses goodness, then
$\vec f_A$
is an exact upper bound of
${\langle {f_\beta } : {\beta \in A} \rangle }$
.
Proof It is straightforward that
$\vec f_A$
is an upper bound. For exactness, suppose that
$g<^\ast \vec f_A$
. Let
$j < \lambda $
witness goodness with respect to A as well as
$g<^\ast \vec f_A$
, and for all i with
$j \le i < \lambda $
, let
$\beta _i \in A$
be such that
$g(i) < f_{\beta _i}(i)$
. If
$\beta = \sup _{j \le i < \lambda } \beta _i$
, then by goodness we have
$g <^\ast f_\beta $
.
Remark. If
$\operatorname {\mathrm {cf}} \alpha \le \operatorname {\mathrm {cf}} \kappa $
, then
${\langle {f_\beta } : {\beta <\alpha } \rangle } $
has no exact upper bound: Let
${\langle {\beta _\xi } : {\xi <\operatorname {\mathrm {cf}} \alpha } \rangle }$
be increasing and cofinal in
$\alpha $
and let
${\langle {S_\xi } : {\xi <\operatorname {\mathrm {cf}} \alpha } \rangle }$
be a partition of
$\operatorname {\mathrm {cf}} \kappa $
into disjoint unbounded sets. Define g such that
$g(i) = f_{\beta _\xi }(i)$
if and only if
$i \in S_\xi $
. Then
$g <^\ast f_\alpha $
, but there is no
$\beta <\alpha $
such that
$g <^\ast f_\beta $
.
Proposition 2.9. If
$\operatorname {\mathrm {cf}} \alpha> \operatorname {\mathrm {cf}} \kappa $
,
$A \subset \alpha $
witnesses goodness of
$\alpha $
, and
$A' \subset A$
is unbounded in
$\alpha $
, then
$\vec f_A =^\ast \vec f_{A'}$
.
Proof It is immediate that
$\vec f_{A'} \le ^\ast \vec f_A$
. Suppose for contradiction that
$\vec f_{A'} <^\ast \vec f_A$
as witnessed by
$j<\lambda $
. Assume that j is also large enough to witnesses goodness with respect to A, which implies that it witnesses goodness with respect to
$A'$
as well. Then for all i with
$j \le i < \lambda $
, there is some
$\beta _i \in A$
such that
$\vec f_{A'}(i) < f_{\beta _i}(i) < \vec f_A(i)$
. Let
$\beta $
be an element of
$A'$
greater or equal to
$\sup _{j \le i < \lambda }\beta _i < \alpha $
. By goodness of
$A'$
,
$i \ge j$
implies that
$f_{\beta _i}(i) \le f_\beta (i)$
, and so we have
$f_\beta (i) \le \vec f_{A'}(i) < f_\beta (i)$
, a contradiction.
Proposition 2.10. Suppose
$\alpha < \kappa ^+$
,
$\operatorname {\mathrm {cf}} \alpha> \operatorname {\mathrm {cf}} \kappa $
and
$A,B \subset \alpha $
both witness goodness of
$\alpha $
. Then
$\vec f_A =^\ast \vec f_B$
.
Proof Assume that j is large enough to witness goodness with respect to both A and B. Use the Sandwich Argument from Proposition 2.1 to find
$A' \subset A$
and
$B' \subset B$
such that
$\vec f_{A'} =^\ast \vec f_{B'}$
. Our result then follows from Proposition 2.9.
Proposition 2.11. Suppose
$\alpha < \kappa ^+$
,
$\operatorname {\mathrm {cf}} \alpha = \operatorname {\mathrm {cf}} \kappa $
, and
$C,D$
are both clubs in
$\alpha $
such that
$\operatorname {\mathrm {ot}} C = \operatorname {\mathrm {ot}} D = \operatorname {\mathrm {cf}} \alpha $
. Then
$f^\Delta _C =^*_\Delta f_D^\Delta $
.
Proof Suppose otherwise. Enumerate
$C\hspace{-1pt} =\hspace{-1pt} {\langle {\beta _i} : {i\hspace{-1pt}<\hspace{-1pt}\operatorname {\mathrm {cf}} \kappa } \rangle }$
and
$D\hspace{-1pt} =\hspace{-1pt} {\langle {\gamma _i} : {i\hspace{-1pt}<\hspace{-1pt} \operatorname {\mathrm {cf}} \kappa } \rangle }$
. Then without loss of generality,
$\{i< \operatorname {\mathrm {cf}} \kappa : \vec f^\Delta _C(i) < \vec f^\Delta _D(i)\}$
is stationary in
$\operatorname {\mathrm {cf}} \kappa $
. Let E be the club
$\{i < \operatorname {\mathrm {cf}} \kappa : \forall j_1,j_2 < i, \exists j^* < i \text { witnessing } f_{\gamma _{j_1}} <^* f_{\gamma _{j_2}}\}$
. Observe that if
$i \in \lim E$
, then
${\langle {f_{\gamma _j}(i)} : {j<i} \rangle }$
is strictly increasing, so for all
$\delta < \sup _{j<i}f_{\gamma _j}(i)$
, there is some
$j'<i$
such that
$\delta < f_{\gamma _{j'}}(i)$
. Let
$S := \lim E \cap \{i< \operatorname {\mathrm {cf}} \kappa : \vec f^\Delta _C(i) < \vec f^\Delta _D(i)\}$
.
Then for all
$i \in S$
, there is some
$j<i$
such that
$\vec f^\Delta _C(i) < f_{\gamma _j}(i)$
. By Fodor’s Lemma, there is a stationary
$T \subset S$
and some
$k < \operatorname {\mathrm {cf}} \kappa $
such that for all
$i \in T$
,
$\vec f_C^\Delta (i) < f_{\gamma _k}(i)$
. If
$\ell $
is large enough that
$\gamma _k < \beta _\ell $
, then there is some m such that for all
$i \ge m$
,
$f_{\gamma _k}(i) < f_{\beta _\ell }(i)$
. If
$i> m, \ell $
, then
$f_{\gamma _k}(i) < f_{\beta _\ell }(i) \le \vec f_C^\Delta (i)$
. But T is of course unbounded, so this implies that we can find an i such that
$f_{\gamma _k}(i) < \vec f_C^\Delta (i) < f_{\gamma _k}(i)$
, a contradiction.
Proof of Lemma 2.6
We are working with a product
$\vec \kappa := \prod _{i<\lambda }\mu _i$
. Let
$\vec g = {\langle {g_\alpha } : { \alpha < \kappa ^+} \rangle }$
be a good scale on this product. Then we define a totally continuous scale
$\vec f = {\langle {f_\alpha } : {\alpha <\kappa ^+} \rangle }$
by induction as follows using the propositions from this section: If
$\alpha = \beta +1$
, choose
$\gamma <\kappa ^+$
large enough that
$f_\beta <^* g_\gamma $
. Then let
$f_\alpha $
be such that
$g_\gamma <^* f_\alpha $
. If
$\alpha $
is a limit and
$\operatorname {\mathrm {cf}} \alpha < \lambda $
, choose any A, a cofinal subset of
$\alpha $
of order-type
$\operatorname {\mathrm {cf}} \alpha $
. Then let
$f_\alpha := \vec f_A$
(Proposition 2.7). If
$\alpha $
is a limit and
$\operatorname {\mathrm {cf}} \alpha = \lambda $
, choose A to be any club subset of
$\alpha $
of order-type
$\operatorname {\mathrm {cf}} \alpha $
. Then let
$f_\alpha := \vec f^\Delta _A$
(Proposition 2.11). Lastly, suppose
$\alpha $
is a limit and
$\operatorname {\mathrm {cf}} \alpha> \lambda $
. Then
$\alpha $
is a good point in terms of
${\langle {f_\beta } : {\beta < \alpha } \rangle }$
because it is cofinally interleaved with
${\langle {g_\beta } : {\beta < \alpha } \rangle }$
. Hence we can choose any cofinal
$A \subset \alpha $
and let
$f_\alpha := \vec f_A$
(Propositions 2.8 and 2.10).
2.2. The construction for weak square
Commencing with the proof of Theorem 1.1, fix a singular
$\kappa $
with cofinality
$\lambda>\omega $
such that
$S^* := \{\delta <\kappa : \square ^*_\delta \text { holds}\}$
is stationary (and of order-type
$\lambda $
). It will be sufficient to assume that for all
$\tau <\kappa $
,
$\tau ^\lambda <\kappa $
, and to assume that
$\prod _{\delta \in S^*} \delta ^+$
carries a good pseudo-scale.
An easy argument using Fodor’s Lemma yields:
Proposition 2.12. There is a club
$E \subset \kappa $
consisting of singular cardinals.
Using Proposition 2.12, let
${\langle {\kappa _i} : {i<\lambda } \rangle }$
be a continuous, cofinal, and strictly increasing sequence of singular cardinals in
$\kappa $
. It follows that
$S:= \{i<\lambda : \kappa _i \in \lim (S^*)\}$
is stationary in
$\lambda $
. Note that
$\prod _{i \in S}\kappa _i^+$
also carries a good pseudo-scale, so we can use Lemma 2.6 to find a totally continuous pseudo-scale
$\vec f ={\langle {f_\alpha } : {\alpha < \kappa ^+} \rangle }$
on the same product.
Let
$\vec {\mathcal C}_i = {\langle {\mathcal {C}_\xi ^i} : {\xi <\kappa _i^+} \rangle }$
witness
$\square ^*_{\kappa _i}$
for all
$i \in S$
. Since
$\kappa _i$
is a limit cardinal for all i, we can assume that for all such i these
$\square ^*_{\kappa _i}$
-sequences have the property that
$\operatorname {\mathrm {ot}} C < \kappa _i$
for all
$C \in \mathcal C_\xi ^i$
,
$\xi <\kappa _i^+$
(see [Reference Cummings2]). If
$\alpha < \kappa ^+$
, we define
$\mathcal F_\alpha $
as follows:
-
• If
$\operatorname {\mathrm {cf}}(\alpha ) \ne \lambda $
, we let
$\mathcal {F}_\alpha $
be the set of functions F such that
$\operatorname {\mathrm {dom}} F = S$
and such that
$\forall i \in S$
,
$F(i) \in \mathcal {C}_{f_\alpha (i)}^i$
. -
• If
$\operatorname {\mathrm {cf}}(\alpha ) = \lambda $
, we let
$\mathcal {F}_\alpha $
be the set of functions F such that
$\operatorname {\mathrm {dom}} F = S$
and such that for some
$h =^*_\Delta f_\alpha $
,
$\forall i \in S$
,
$F(i) \in \mathcal {C}_{h(i)}^i$
.
Regardless of whether or not
$\operatorname {\mathrm {cf}}(\alpha )=\lambda $
, we will say that some
$h \in \prod _{i \in S}\kappa _i^+$
witnesses
$F \in \mathcal {F}_\alpha $
if for all
$i \in S$
,
$F(i) \in \mathcal {C}_{h(i)}^i$
.
For each
$\alpha < \kappa ^+$
and
$F \in \mathcal F_\alpha $
, we define
$C_F \subset \alpha $
as follows:
-
• If
$\beta < \alpha $
and
$\operatorname {\mathrm {cf}} \beta \ne \lambda $
, then
$\beta \in C_F$
if and only if there is some
$j<\lambda $
such that for all
$i \in S \setminus j$
,
$f_\beta (i) \in F(i)$
. -
• If
$\beta < \alpha $
and
$\operatorname {\mathrm {cf}} \beta = \lambda $
, then
$\beta \in C_F$
if and only if the set of limit ordinals
$\gamma \in C_F$
with
$\operatorname {\mathrm {cf}}(\gamma )<\lambda $
is unbounded in
$\beta $
.
Now we define our
$\square _\kappa ^*$
-sequence at
$\alpha $
depending on the cofinality:
-
• If
$\operatorname {\mathrm {cf}} \alpha < \lambda $
, then
$\mathcal C_\alpha := \{C_F: F \in \mathcal F_\alpha \text { and }C_F \text { is unbounded in }\alpha \} \cup \{C \subset \alpha : C \text { is a club in }\alpha \text { and }\operatorname {\mathrm {ot}} C < \lambda \}$
. -
• If
$\operatorname {\mathrm {cf}} \alpha = \lambda $
, choose a club
$C \subset \alpha $
such that
$\operatorname {\mathrm {ot}} C = \lambda $
and let
$\mathcal C_\alpha := \{C_F: F \in \mathcal F_\alpha \text { and }C_F \text { is unbounded in }\alpha \} \cup \{C\}$
. -
• If
$\operatorname {\mathrm {cf}} \alpha> \lambda $
, let
$\mathcal C_\alpha := \{C_F: F \in \mathcal F_\alpha \}$
.
Lemma 2.13. For all
$\alpha \in \lim (\kappa ^+)$
and
$C \in \mathcal {C}_\alpha $
, C is closed.
Proof It is enough to show that for all
$\alpha \in \lim (\kappa ^+)$
and
$F \in \mathcal F_\alpha $
,
$C_F$
is closed. The proof of this lemma does not depend on whether or not
$\operatorname {\mathrm {cf}}(\alpha ) = \lambda $
; that is, it does not depend on whether
$F \in \mathcal {F}_\alpha $
is witnessed specifically by
$f_\alpha $
or some
$h =^\ast _\Delta f_\alpha $
. Let
${\langle {\beta _\xi } : {\xi <\tau } \rangle } {\subseteq } C_F$
be a strictly increasing sequence with supremum
$\beta <\alpha $
where
$\tau $
is regular. Without loss of generality, we can assume that
$\operatorname {\mathrm {cf}}(\beta _\xi )<\lambda $
for all
$\xi <\tau $
. For each
$\xi <\tau $
, let
$j_\xi $
witness that
$\beta _\xi \in C_F$
, i.e., for all
$i \ge j_\xi $
,
$f_{\beta _\xi }(i) \in F(i)$
.
Case 1
$: \tau <\lambda $
. If
$j'= \sup _{\xi <\tau }j_\xi $
, then for all
$i \ge j'$
, we have
$\sup _{\xi <\tau } f_{\beta _\xi }(i) \in F(i)$
. By continuity, there is also some
$j"$
such that for all
$i \ge j"$
,
$f_\beta (i) = \sup _{\xi <\tau } f_{\beta _\xi }(i)$
. Hence, if j is larger than
$j'$
and
$j"$
, then j witnesses that
$\beta \in C_F$
by closure of
$F(i)$
for
$i \in S$
.
Case 2
$: \tau> \lambda $
. By the Pigeonhole Principle there is some unbounded
$Z \subset \tau $
and some
$j'<\lambda $
such that
$j_\xi = j'$
for all
$\xi \in Z$
. By Proposition 2.1, there is some
$j"$
and some
$Z' \subset Z$
such that
$\{\beta _\xi : \xi \in Z'\}$
and
$j"$
witness goodness. It then follows by continuity that for all
$i \ge j"$
,
$f_\beta (i) = \sup _{\xi \in Z'}f_{\beta _\xi }(i) \in \lim F(i)$
. If
$j \ge j',j"$
, then j witnesses that
$\beta \in C_F$
as in the previous case.
Case 3
$: \tau = \lambda $
. We can assume that
$\operatorname {\mathrm {cf}}(\beta _\xi ) < \lambda $
for all
$\xi <\lambda $
. Then closure follows from Case 1 by definition.
The following lemma is where we first directly use the hypothesis that
$\operatorname {\mathrm {cf}}(\kappa )>\omega $
.
Lemma 2.14. For all
$\alpha \in \lim (\kappa ^+)$
,
$C \in \mathcal C_\alpha $
is unbounded in
$\alpha $
.
Proof It is sufficient to show that if
$\operatorname {\mathrm {cf}} \alpha> \lambda $
, then
$C_F$
is unbounded in
$\alpha $
for an arbitrary
$F \in \mathcal F_\alpha $
. We will use the fact that
$F \in \mathcal {F}_\alpha $
can only be witnessed by
$f_\alpha $
. Consider some
$\bar \alpha <\alpha $
. We will find an element of
$C_F$
larger than
$\bar \alpha $
. By induction we define a sequence of ordinals
${\langle {\alpha _n} : {n<\omega } \rangle }$
in the interval
$(\bar \alpha ,\alpha )$
, a
$<^\ast $
-increasing sequence of functions
${\langle {g_n} : {n<\omega } \rangle }$
in
$\prod _{i \in S}\kappa _i^+$
, and an undirected list of ordinals
${\langle {j_n} : {n<\omega } \rangle }$
in
$\lambda $
.
Let
$\alpha _0 \in (\bar {\alpha },\alpha )$
and
$g_0 <^* f_\alpha $
be arbitrary. Suppose that
$\alpha _n$
and
$g_n$
are defined. Let
$g_{n+1}$
be defined so that for all
$i<\lambda $
,
$g_{n+1}(i)$
is an element of
$F(i)$
larger than
$f_{\alpha _n}(i)$
. Using the facts that
$g_{n+1}<^\ast f_\alpha $
and that
$f_\alpha $
is an exact upper bound of
${\langle {f_\beta } : {\beta <\alpha } \rangle }$
, find
$\alpha _{n+1}$
so that
$g_{n+1} <^\ast f_{\alpha _{n+1}}$
, and let
$j_{n+1}<\lambda $
witness this.
Let
$\beta = \sup _{n<\omega }\alpha _n$
, which in particular is larger than
$\bar \alpha $
. We claim that
$\beta \in C_F$
as witnessed by
$j:=\sup _{n<\omega }j_n<\lambda $
. For each
$i<\lambda $
such that
$i \ge j$
,
${\langle {g_n(i)} : {i<\omega } \rangle }$
and
${\langle {f_{\alpha _n}(i)} : {n<\omega } \rangle }$
interleave each other, so
$\sup _{n<\omega }f_{\alpha _n}(i) \in \lim F(i)$
for such i. For sufficiently large i,
$f_{\beta }(i) = \sup _{n<\omega }f_{\alpha _n}(i)$
by continuity, so this completes the proof.
Lemma 2.15. For all
$\alpha \in \lim (\kappa ^+)$
and
$C \in \mathcal C_\alpha $
, if
$\beta \in \lim C$
, then
$C \cap \beta \in \mathcal C_\beta $
.
Proof The lemma is only substantial if
$C = C_F$
for some
$F \in \mathcal F_\alpha $
, and it does not depend on whether
$\operatorname {\mathrm {cf}}(\alpha )=\lambda $
. By assumption
$C_F$
is unbounded in
$\beta $
, so Lemma 2.13 implies that
$\beta \in C_F$
.
Case 1
$: \operatorname {\mathrm {cf}} \beta \ne \lambda $
: Let
$j<\lambda $
witness
$\beta \in \lim C_F$
, meaning that if
$i \ge j$
then
$f_\beta (i) \in \lim F(i)$
. By the coherence of
$\vec {\mathcal C}^i$
for
$i \in S$
, it follows that
$F(i) \cap f_\beta (i) \in {\mathcal C}_{f_\beta (i)}^i$
for such i. Let
$F'$
be a function with domain S such that
$F'(i) = F(i) \cap f_\beta (i)$
for all
$i \ge j$
and such that
$F'(i) \in \mathcal C_{f_\beta (i)}^i$
for
$i \in (S \cap \lambda \setminus j)$
in particular. Then
$F' \in \mathcal F_\beta $
and
$C_{F'}$
is unbounded in
$\beta $
, so
$C_{F'} \in \mathcal C_\beta $
. If
$\gamma < \beta $
, let
$j'<\lambda $
witness
$f_\gamma <^\ast f_\beta $
. Then if
$i \ge j,j'$
, it follows that
$f_\gamma (i) \in F(i)$
if and only if
$f_\gamma (i) \in F'(i)$
. We conclude that
$C_F \cap \beta = C_{F'}$
.
Case 2
$: \operatorname {\mathrm {cf}} \beta = \lambda $
: Choose a sequence
${\langle {\beta _i} : {i<\lambda } \rangle } \subset C_F \cap \beta $
; by closure (Lemma 2.13, Case 1) we can assume that
${\langle {\beta _i} : {i<\lambda } \rangle }$
is closed and unbounded in
$\lambda $
, and that
$\operatorname {\mathrm {cf}}(\beta _i)<\lambda $
for all
$i<\lambda $
. By Proposition 2.11, we also know that
$f_\beta =^*_\Delta (\vec f {\upharpoonright } \beta )^\Delta _{{\langle {\beta _i} : {i<\lambda }} \rangle }$
, i.e
$.,$
that there is a club
$E \subset \lambda $
such that for all
$i \in E$
,
$f_\beta (i) = \sup _{j<i}f_{\beta _j}(i)$
. Let D be a club such that
$D \subseteq E$
and such that for all
$i \in D,j<i$
, there is some
$j'<i$
witnessing that
$\beta _j \in C_F$
, and moreover such that for all
$i \in D,j_1,j_2<i$
, there is some
$j<i$
witnessing that
$f_{\beta _{j_1}}<^* f_{\beta _{j_2}}$
. It follows that for all
$i \in D$
and
$j<i$
,
$f_{\beta _j}(i) \in \lim F(i)$
, and therefore that for all
$i \in D$
,
$f_\beta (i) \in \lim F(i)$
. Then let
$F'$
be defined so that
$F'(i) = F(i) \cap f_{\beta }(i)$
for
$i \in D \cap S$
and
$F'(i) = F(i)$
for
$i \in S \setminus D$
. Then it follows that
$C_F \cap \beta = C_{F'}$
: in particular, if
$\gamma \in C_{F'}$
, then
$f_\gamma $
is dominated by
$f_\beta $
on a club, so it must be the case that
$\gamma <\beta $
. Hence we find that
$F' \in \mathcal {F}_\beta $
is witnessed by h such that
$h(i)=f_\beta (i)$
for
$i \in D$
and
$h(i) = h'(i)$
for the
$h'$
witnessing
$F \in \mathcal {F}_\alpha $
(hence
$h =^*_\Delta f_\beta $
). Therefore we have shown that
$C_F \cap \beta \in \mathcal {C}_\beta $
.
We use the hypothesis that
$\operatorname {\mathrm {cf}}(\kappa )>\omega $
again in the next two lemmas, specifically in the application of Fodor’s Lemma.
Lemma 2.16. For all
$\alpha \in \lim (\kappa ^+)$
and
$C \in \mathcal C_\alpha $
,
$\operatorname {\mathrm {ot}} C < \kappa $
.
Proof It is sufficient to show that
$\operatorname {\mathrm {ot}} C_F < \kappa $
for all
$F \in \mathcal F_\alpha $
and all
$\alpha < \kappa ^+$
(independently of whether
$\operatorname {\mathrm {cf}}(\alpha ) = \lambda $
). Recall that we assumed that the
$\square _{\kappa _i}^*$
-sequences
${\langle {\mathcal C_\xi ^i} : {i<\kappa _i^+} \rangle }$
were defined so that for all for all
$i<\lambda , \xi <\kappa _i^+,C \in \mathcal C_\xi ^i$
,
$\operatorname {\mathrm {ot}} C <\kappa _i$
.
Fix
$\alpha <\kappa ^+$
. For every
$i \in S$
, there is some
$j<i$
such that
$\operatorname {\mathrm {ot}} F(i) < \kappa _j$
. This means that there is a stationary
$T {\subseteq } S$
and some k such that for all
$i \in T$
,
$\operatorname {\mathrm {ot}} F(i) < \kappa _k$
. If
$\beta \in C_F$
and
$i \in T$
, let
$g_\beta (i) = \operatorname {\mathrm {ot}} (F(i) \cap f_\beta (i))$
for all i such that
$f_\beta (i) \in F(i)$
and
$0$
otherwise. The set
$\{g_\beta :\beta \in C_F\}$
has size
$\kappa _k^{\lambda }<\kappa $
(we assumed this bit of cardinal arithmetic), so it is enough to observe that if
$\beta ,\beta ' \in C_F$
and
$\beta <\beta '$
, then
$g_\beta $
and
$g_{\beta '}$
are distinct.
Lemma 2.17. For all
$\alpha \in \lim (\kappa ^+)$
,
$|\mathcal C_\alpha | \le \kappa $
.
Proof Our assumption that
$\tau ^\lambda < \kappa $
for all
$\tau < \kappa $
implies that
$|\{C \subset \alpha : \operatorname {\mathrm {ot}} C < \lambda \}| = \kappa $
, so it is enough to show that
$|\{C_F:F \in \mathcal {F}_\alpha \}| \le \kappa $
for all
$\alpha \in \lim (\kappa ^+$
).
Fix
$\alpha \in \lim (\kappa ^+)$
. We first argue for the case in which
$\operatorname {\mathrm {cf}}(\alpha ) \ne \lambda $
. For all
$i \in S$
enumerate
$\mathcal C^i_{f_\alpha (i)} = {\langle {C^i_\zeta } : {\zeta <\kappa _i} \rangle }$
. Given a stationary set
$T \subset S$
and
$\zeta < \kappa $
, let
$$\begin{align*}X_T^k = \{F \in \mathcal{F}_\alpha : \forall i \in T, \exists \zeta < \kappa_k \text{ such that }F(i) = C^i_\zeta \text{ and }\operatorname{\mathrm{ot}}(C^i_\zeta) < \kappa_k\}. \end{align*}$$
We claim that for all
$F \in \mathcal F_\alpha $
, there are
$T \subset S$
and
$k < \lambda $
such that
$C_F \in X_T^k$
. Let
$F \in \mathcal F_\alpha $
. For each F and
$i \in S$
, there is some
$j<i$
such that we have
$F(i) = C^i_\zeta $
for some
$\zeta < \kappa _j$
and
$\operatorname {\mathrm {ot}}(C^i_\zeta )<\kappa _j$
as well. It follows that there is a stationary
$T \subset S$
and
$k < \lambda $
such that for all
$i \in T$
,
$F(i) = C^i_\zeta $
and
$\operatorname {\mathrm {ot}}(C^i_\zeta )<\kappa _k$
for some
$\zeta < \kappa _k$
.
Because
$2^\lambda = \lambda ^\lambda < \kappa $
, there are at most
$\kappa $
-many
$X_T^k$
’s. Therefore it remains to show that for all such
$T,k$
, that
$|\{C_F:F \in X_T^k\}| \le \kappa $
. Let
$G_F$
be the set of functions
$g_\beta =f_\beta {\upharpoonright } T$
for all
$\beta \in C_F$
. If
$\beta \ne \beta '$
, then
$g_\beta \ne g_{\beta '}$
, so if
$F' \ne F$
then
$G_F \ne G_{F'}$
. Now, for
$i \in T$
, let
$R^k_T(i) = \bigcup _{\zeta <\kappa _k}C_\zeta ^i$
. Then for all
$F \in F^k_T$
,
$G_F \subseteq \prod _{i \in T} R^k_T(i)$
. Moreover,
$\prod _{i \in T} R^k_T(i)$
has cardinality
$\kappa _k^\lambda < \kappa $
. It follows that
$|\{C_F:F \in X_T^k\}| \le \kappa $
.
Now we comment on the case in which
$\operatorname {\mathrm {cf}}(\alpha ) = \lambda $
. By intersecting with an appropriate club, we can see that for all
$F \in \mathcal {F}_\alpha $
, there is some stationary
$S' \subset S$
such that for all
$i \in S'$
,
$F(i) \in C^i_{f_\alpha (i)}$
. The argument above can be done for all
$F \in \mathcal {F}_\alpha $
such that there is an h witnessing
$F \in \mathcal {F}_\alpha $
where
$h {\upharpoonright } S' = f_\alpha {\upharpoonright } S'$
. Since
$2^\lambda < \kappa $
, and we only need to consider
$2^\lambda $
-many possible
$S'$
, this is sufficient.
This finishes the proof of Theorem 1.1.
2.3. Sketching the construction for partial square
Now we will sketch a proof of Theorem 1.4.
This can be proved with the same techniques as the previous theorem, and the setup is basically the same: We fix a singular strong limit
$\kappa $
with cofinality
$\lambda>\omega $
such that
$\{\delta <\kappa : \square _\delta \text { holds}\}$
is stationary (and of order-type
$\lambda $
). Let
${\langle {\kappa _i} : {i<\lambda } \rangle }$
be continuous, cofinal, and strictly increasing in
$\kappa $
. We find that
$S:= \{i<\lambda : \square _{\kappa _i} \text { holds}\}$
is stationary in
$\lambda $
, and we can construct a totally continuous scale
$\vec f = {\langle {g_\alpha } : {\alpha <\kappa ^+} \rangle }$
on
$\prod _{i \in S} \kappa _i^+$
. Let
$\mathcal C_i = {\langle {C_\xi ^i} : {\xi <\kappa _i^+} \rangle }$
witness
$\square _{\kappa _i}$
for all
$i \in S$
. By Proposition 2.12, we can again assume that
$\operatorname {\mathrm {ot}} C_\xi ^i<\kappa _i$
for all
$\xi <\kappa _i^+,i<\lambda $
. Now we can define the clubs of which our square sequence will consist. For each
$\alpha \in \kappa ^+ \cap \operatorname {\mathrm {cof}}(>\lambda )$
, let:
$$\begin{align*}X_\alpha := {\langle {\beta<\alpha} : {\{i<\lambda:f_\beta(i) \in \lim C^i_{f_\alpha(i)}\} \text{ is co-bounded in }S} \rangle}. \end{align*}$$
Then we have an analog of Lemma 2.13:
Lemma 2.18. For all
$\alpha \in \lim (\kappa ^+)$
, if
${\langle {\beta _\xi } : {\xi <\tau } \rangle } \subset X_\alpha $
’s and
$\tau \ne \lambda $
, then
$\sup _{\xi < \tau }\beta _\xi \in X_\alpha $
.
Then let
$C_\alpha $
be the closure of
$X_\alpha $
inside
$\alpha $
. The partial square sequence will be the sequence
${\langle {C_\alpha } : { \alpha \in \kappa ^+ \cap \operatorname {\mathrm {cof}}(>\lambda )} \rangle }$
. Proofs of the various lemmas are analogous. Coherence for the case
$\operatorname {\mathrm {cf}}(\beta )=\lambda $
is easier since no witness needs to be constructed.
Lemma 2.19. For all
$\alpha ,\beta \in \lim (\lambda ^+)$
, if
$\gamma \in \lim C_\alpha , \lim C_\beta $
, then
$C_\alpha \cap \gamma = C_\beta \cap \gamma $
.
Proof Suppose
$\gamma $
has cofinality
$\tau $
.
Case 1
$: \tau \ne \mu $
. Then
$X_\alpha $
and
$X_\beta $
are both unbounded in
$\gamma $
, so Lemma 2.18 implies that
$\gamma \in X_\alpha \cap X_\beta $
. We argue as in Lemma 2.15 to show that
$X_\alpha \cap \gamma = X_\beta \cap \gamma $
, so the result follows.
Case 2
$: \tau = \mu $
. Let
${\langle {\gamma _\xi } : {\xi <\tau } \rangle }$
be a strictly increasing and continuous sequence converging to
$\gamma $
such that for all
$\xi <\tau $
,
$C_\alpha \cap (\gamma _\xi ,\gamma _{\xi +1})$
and
$C_\beta \cap (\gamma _\xi ,\gamma _{\xi +1})$
are both non-empty. For each limit
$\eta < \tau $
,
$C_\alpha \cap \gamma _\eta = C_\beta \cap \gamma _\eta $
by Case 1. Therefore,
$C_\alpha \cap \gamma = C_\beta \cap \gamma $
.
Lemma 2.20. For all
$\alpha \in \lim (\lambda ^+)$
such that
$\operatorname {\mathrm {cf}} \alpha>\operatorname {\mathrm {cf}} \lambda $
,
$C_\alpha $
is unbounded in
$\alpha $
.
It is sufficient to show that if
$\operatorname {\mathrm {cf}} \alpha> \operatorname {\mathrm {cf}} \lambda $
, then
$X_\alpha $
is unbounded in
$\alpha $
. The argument is as in Lemma 2.14.
Lemma 2.21. For all
$\alpha \in \lim (\lambda ^+)$
,
$\operatorname {\mathrm {ot}} C_\alpha < \lambda $
.
This is argued as in Lemma 2.16.
2.4. Further directions
We conclude with the following:
Question 1. Suppose that
$\kappa $
is a singular strong limit of uncountable cofinality
$\lambda $
such that
$S:=\{\delta < \kappa : \square _\delta ^* \text { holds}\}$
is stationary. Does
$\prod _{\delta \in S} \delta ^+$
carry a good pseudo-scale?
Note that we have:
Fact 2.22. If
$\kappa $
is singular, then
$\square ^*_\kappa $
implies that all pseudo-scales on
$\kappa $
are good.Footnote
2
By Theorem 1.1, this question is almost equivalent (modulo a generalization and a strong limit assumption) to the question of Golshani mentioned above: a positive answer would mean that these hypotheses imply
$\square _\kappa ^*$
, and a negative answer would mean that
$\square _\kappa ^*$
consistently fails in conjunction with these hypotheses.
Acknowledgements
I proved an early version of Theorem 1.4 while being supported by Sy-David Friedman’s FWF grant in Vienna, and I want to thank him for many helpful conversations. I also thank Dima Sinapova for many helpful conversations and critical readings of early versions of the paper. Also, I thank Chris Lambie-Hanson for catching mistakes in the original arXiv version and for referring me to a note that Assaf Rinot had written that built on this work [Reference Rinot12]. Finally, I thank Sittinon Jirattikansakul for catching additional mistakes in the original version. Thanks also to the anonymous referee for improving the manuscript.
