Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T08:53:31.115Z Has data issue: false hasContentIssue false
  • English
  • Français

On generalized computational complexity1

Published online by Cambridge University Press:  12 March 2014

Barry E. Jacobs
Get access Rights & Permissions [Opens in a new window]

Extract

If one regards an ordinal number as a generalization of a counting number, then it is natural to begin thinking in terms of computations on sets of ordinal numbers. This is precisely what Takeuti [22] had in mind when he initiated the study of recursive functions on ordinals. Kreisel and Sacks [9] too developed an ordinal recursion theory, called metarecursion theory, which specialized to the initial segment of the ordinals bounded by 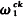(the first nonconstructive ordinal).

The notion of admissibility was introduced by Kripke [11] and Platek [14] and served to generalize metarecursion theory. Kripke called ordinal α admissible if it satisfied certain closure properties of infinitary computations. It was shown that admissibility could be equivalently formulated in terms of the replacement schema of ZF set theory and that α = 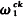is an admissible ordinal. The study of a recursion theory on an initial segment of the ordinals bounded by some arbitrary admissible α became known as α-recursion theory.

Kripke [10] employed a Gödel numbering scheme to perform an arithmetiza-tion of α -recursion theory and created an analogue to Kleene's T-predicate (cf. [8]) of ordinary recursion theory (o.r.t.). The T-predicate then served as the basis for showing that analogues of the major results of unrelativized o.r.t. held in α-recursion theory; namely, the α-Enumeration Theorem, 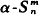T Theorem, α-Recursion Theorem, and α-Universal Function Theorem.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 1 , March 1977 , pp. 47 - 58
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The results in this paper appear in the author's Ph.D. dissertation supervised by Martin D. Davis at the Courant Institute, New York University.

References

REFERENCES

[1]Blum, M., A machine-independent theory of the complexity of recursive functions, Journal of the Association for Computing Machinery, vol. 14 (1967), pp. 322–336.CrossRefGoogle Scholar
[2]Borodin, A., Computational complexity and the. existence of complexity gaps, Journal of the Association for Computing Machinery, vol. 19 (1972), pp. 158–174.CrossRefGoogle Scholar
[3]Constable, R., The operator gap, Journal of the Association for Computing Machinery, vol. 19 (1972), pp. 175–183.CrossRefGoogle Scholar
[4]Gödel, K., The consistency of the continuum hypothesis, Princeton University Press, Princeton, New Jersey, 1940.CrossRefGoogle Scholar
[5]Harrington, L. A., Contributions to recursion theory on higher types, Ph.D. Thesis, M.I.T., Cambridge, Massachusetts, 1973.Google Scholar
[6]Hartmanis, J. and Hopcroft, J., An overview of the theory of computational complexity, Journal of the Association for Computing Machinery, vol. 18 (1971), pp. 444–475.CrossRefGoogle Scholar
[7]Jacobs, B. E., α-computational complexity, Technical Report IMM 408, Ph.D. Thesis, Courant Institute, New York University, New York, New York, 1975.Google Scholar
[8]Kleene, S. C., Introduction to metamathematics, North-Holland, Amsterdam, 1971.Google Scholar
[9]Kreisel, G. and Sacks, G., Metarecursive sets, this Journal, vol. 30 (1965), pp. 318–338.Google Scholar
[10]Kripke, S., The theory of transfinite recursions, (unpublished), class notes by A. Thomas Tymoczko.Google Scholar
[11]Kripke, S., Transfinite recursions on admissible ordinals. I, II, Abstracts, this Journal, vol. 29 (1964), pp. 161–162.Google Scholar
[12]Lerman, M., On suborderings of the α-recursively enumerable α-degrees, Annals of Mathematical Logic, vol. 4 (1972), pp. 369–392.CrossRefGoogle Scholar
[13]McCreight, E. and Meyer, A., Classes of computable functions defined by bounds on computation, preliminary report, Proceedings of the Association for Computing Machinery Symposium on Theory of Computing, 1969, pp. 79–88.Google Scholar
[14]Platek, R., Foundations of recursion theory, Ph.D. Thesis, Stanford University, 1966.Google Scholar
[15]Rabin, M. O., Degrees of difficulty of computing a function and a partial ordering of recursive sets, Technical Report, 2, Hebrew University, Jerusalem, Israel, 1960.Google Scholar
[16]Rogers, H., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[17]Sacks, G. E., Higher recursion theory, Springer, Berlin (to appear).Google Scholar
[18] Sacks, G. E. and Simpson, S., The α-finite injury method, Annals of Mathematical Logic, vol. 4 (1972), pp. 343–368.CrossRefGoogle Scholar
[19]Shore, R., Splitting an α-recursively enumerable set, Transactions of the American Mathematical Society, vol. 204 (1975), pp. 65–77.Google Scholar
[20]Shore, R., Σn sets which are Δn-incomparable (uniformly), this Journal, vol. 39 (1974), pp. 295–304.Google Scholar
[21]Simpson, S., Degree theory on admissible ordinals, Generalized recursion theory (Fenstad, J. and Hinman, P., Editors), North-Holland, Amsterdam, 1972, pp. 165–193.Google Scholar
[22]Takeuti, G., On the recursive functions of ordinals, Journal of the Mathematical Society of Japan, vol. 12 (1960), pp. 119–128.CrossRefGoogle Scholar
[23]Young, P., Easy constructions in complexity theory: gap and speed-up theorems, Proceedings of the American Mathematical Society, vol. 37 (1973), pp. 555–563.CrossRefGoogle Scholar