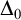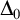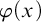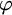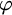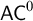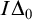1 Introduction
1.1 Parameterized complexity
While classical complexity theory measures computational resources by functions in the input length n alone, parameterized complexity theory additionally takes into account a parameter k associated with inputs.Footnote
1
The motivation is to focus attention on inputs with relatively small parameter
![]() $k \ll n$
, namely, one asks for algorithms that are efficient on such inputs. If “efficient” means polynomial time, this leads to the class
$k \ll n$
, namely, one asks for algorithms that are efficient on such inputs. If “efficient” means polynomial time, this leads to the class
![]() $\mathsf {FPT}$
: decidable problems that admit a polynomial time algorithm that is correct on inputs satisfying
$\mathsf {FPT}$
: decidable problems that admit a polynomial time algorithm that is correct on inputs satisfying
![]() $g(k)\leqslant n$
for some computable
$g(k)\leqslant n$
for some computable
![]() $g:\mathbb {N}\to \mathbb {N}$
, or equivalently, an algorithm correct on all inputs with runtime
$g:\mathbb {N}\to \mathbb {N}$
, or equivalently, an algorithm correct on all inputs with runtime
![]() $f(k)\cdot n^{O(1)}$
for some computable
$f(k)\cdot n^{O(1)}$
for some computable
![]() $f:\mathbb {N}\to \mathbb {N}$
. If “efficient” means
$f:\mathbb {N}\to \mathbb {N}$
. If “efficient” means
![]() $\mathsf {AC}^0$
, it leads to the class
$\mathsf {AC}^0$
, it leads to the class
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
. Here, and throughout, by
$\mathsf {para}\text {-}\mathsf {AC}^0$
. Here, and throughout, by
![]() $\mathsf {AC}^0$
we mean dlogtime uniform
$\mathsf {AC}^0$
we mean dlogtime uniform
![]() $\mathsf {AC}^0$
.
$\mathsf {AC}^0$
.
Many problems have natural parameters in the sense that the focus on inputs with relatively small parameters is practically or theoretically well motivated. Two examples:


The parameterized complexity of both problems is wide open. Before entering their discussion we note a special property: the problems are almost tally, in that inputs are long strings of 1’s padded with relatively short binary strings. This concept is key to the approach taken here.
1.2 The parameterized halting problem
The importance of p-Halt is derived from its close connections to central problems in proof complexity and descriptive complexity theory [Reference Chen and Flum10]: the hypotheses that a certain logic considered by Gurevich [Reference Gurevich24] does not capture
![]() $\mathsf {PTIME}$
, and that p-optimal propositional proof systems do not exist [Reference Krajícek and Pudlák30] are both equivalent to the hypothesis that
$\mathsf {PTIME}$
, and that p-optimal propositional proof systems do not exist [Reference Krajícek and Pudlák30] are both equivalent to the hypothesis that ![]() cannot be decided in time
cannot be decided in time
![]() $n^{f(k)}$
where
$n^{f(k)}$
where
![]() $k:=|\mathbb M|$
and
$k:=|\mathbb M|$
and
![]() $f: \mathbb {N}\to \mathbb {N}$
is any function.Footnote
2
So far, however, such algorithms have been ruled out only under a certain very strong non-standard complexity-theoretic hypothesis and only for computable f [Reference Chen and Flum9, Reference Chen and Flum10]. Thus, lower bounds on
$f: \mathbb {N}\to \mathbb {N}$
is any function.Footnote
2
So far, however, such algorithms have been ruled out only under a certain very strong non-standard complexity-theoretic hypothesis and only for computable f [Reference Chen and Flum9, Reference Chen and Flum10]. Thus, lower bounds on ![]() are poorly understood and of fundamental interest.
are poorly understood and of fundamental interest.
A seemingly modest and natural starting point is the following.
Conjecture 1.1.
![]() .
.
This conjecture is highly plausible and might appear to be within reach because
![]() $\mathsf {AC}^0$
is well-understood and, in particular, [Reference Chen and Flum11] establishes (unconditional)
$\mathsf {AC}^0$
is well-understood and, in particular, [Reference Chen and Flum11] establishes (unconditional)
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
lower bounds for many well-studied parameterized problems. It deserves some genuine interest because its failure implies that
$\mathsf {para}\text {-}\mathsf {AC}^0$
lower bounds for many well-studied parameterized problems. It deserves some genuine interest because its failure implies that
![]() $\mathsf {AC}^0$
, or equivalently,
$\mathsf {AC}^0$
, or equivalently,
![]() $(+, \times )$
-invariant
$(+, \times )$
-invariant
![]() $\mathsf {FO}$
is captured by some logic. However, we failed to prove the conjecture after years of attempts and only now understand why: it implies that nondeterministic exponential time
$\mathsf {FO}$
is captured by some logic. However, we failed to prove the conjecture after years of attempts and only now understand why: it implies that nondeterministic exponential time
![]() $\mathsf {NE}$
is distinct from the linear time hierarchy
$\mathsf {NE}$
is distinct from the linear time hierarchy
![]() $\mathsf {LINH}$
. This connection can be further tightened by considering the following variant of
$\mathsf {LINH}$
. This connection can be further tightened by considering the following variant of ![]() :
:

Accepting in exactly n steps means that there exists an accepting computation that has exactly n steps. While the classical problems underlying ![]() and
and ![]() are easily seen to be equivalent (see Example 3.6), we shall see that their parameterized versions behave quite differently. In fact,
are easily seen to be equivalent (see Example 3.6), we shall see that their parameterized versions behave quite differently. In fact, ![]() appears to be harder than
appears to be harder than ![]() , and is the hardest among all almost tally problems in
, and is the hardest among all almost tally problems in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
, the parameterized analogue of
$\mathsf {para}\text {-}\mathsf {NP}$
, the parameterized analogue of
![]() $\mathsf {NP}$
. We refer to Section 7 for a discussion. We show:
$\mathsf {NP}$
. We refer to Section 7 for a discussion. We show:
Theorem 1.2.
-
(i)
 if and only if
if and only if
 $\mathsf {NE}\subseteq \mathsf {LINH}$
.
$\mathsf {NE}\subseteq \mathsf {LINH}$
. -
(ii)
 implies
implies  .
.
1.3
 $\Delta _0$
truth
$\Delta _0$
truth
Deciding the truth of
![]() $\Delta _0$
formulas is a fundamental problem of mathematical logic. The choice of the parameter shifts attention to inputs where n is much larger than
$\Delta _0$
formulas is a fundamental problem of mathematical logic. The choice of the parameter shifts attention to inputs where n is much larger than
![]() $|\varphi |$
. This is a natural focus. Classical work of Paris and Dimitracopolous [Reference Paris and Dimitracopoulos34] took n to be nonstandard and related the complexity of truth definitions for
$|\varphi |$
. This is a natural focus. Classical work of Paris and Dimitracopolous [Reference Paris and Dimitracopoulos34] took n to be nonstandard and related the complexity of truth definitions for
![]() $\Delta _0$
-formulas to the complexity-theoretic hypotheses that
$\Delta _0$
-formulas to the complexity-theoretic hypotheses that
![]() $\mathsf {LINH}$
or
$\mathsf {LINH}$
or
![]() $\mathsf {PH}$
does not collapse. Wilkie proved a weak version of the former hypothesis by showing that
$\mathsf {PH}$
does not collapse. Wilkie proved a weak version of the former hypothesis by showing that ![]() restricted to quantifier-free formula inputs can be decided in space
restricted to quantifier-free formula inputs can be decided in space
![]() $f(k)+O(\log n)$
where
$f(k)+O(\log n)$
where
![]() $k:= |\varphi |$
is the parameter and
$k:= |\varphi |$
is the parameter and
![]() $f:\mathbb {N}\to \mathbb {N}$
a computable function [Reference Wilkie36, proof of Lemma 3.1]. The straightforward algorithm decides
$f:\mathbb {N}\to \mathbb {N}$
a computable function [Reference Wilkie36, proof of Lemma 3.1]. The straightforward algorithm decides ![]() in space
in space
![]() $f(k)\cdot \log n$
. Can it be decided in space
$f(k)\cdot \log n$
. Can it be decided in space
![]() ${f(k)+ O(\log n)}$
? Maybe with nondeterminism? Can it be decided in time
${f(k)+ O(\log n)}$
? Maybe with nondeterminism? Can it be decided in time
![]() $f(k)\cdot n^{O(1)}$
, i.e., is it in
$f(k)\cdot n^{O(1)}$
, i.e., is it in
![]() $ \mathsf {FPT}$
? Maybe with nondeterminism, i.e., is it in
$ \mathsf {FPT}$
? Maybe with nondeterminism, i.e., is it in
![]() $ \mathsf {para}\text {-}\mathsf {NP}$
?
$ \mathsf {para}\text {-}\mathsf {NP}$
?
Our main result (Theorem 4.3) shows that such upper bounds on the parameterized complexity of ![]() imply lower bounds in classical complexity theory. Notably,
imply lower bounds in classical complexity theory. Notably,
Theorem 1.3. If ![]() , then
, then
![]() $\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
$\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
The proof relies on our analysis of ![]() and the following unconditional lower bound:
and the following unconditional lower bound:
Theorem 1.4.
![]() .
.
The proof is based on diagonalization or, more specifically, the undefinability of truth. Furthermore, it relies on the classical result [Reference Barrington, Immerman and Straubing6] of descriptive complexity theory that, roughly speaking, equates (uniform)
![]() $\mathsf {AC}^0$
and first-order logic with built-in arithmetic.
$\mathsf {AC}^0$
and first-order logic with built-in arithmetic.
1.4 The MRDP theorem
Theorem 1.3 yields some information concerning the provability of the Matiyasevich-Robinson-Davis-Putnam (MRDP) theorem (see [Reference Davis14] for an account) in bounded arithmetic. This theorem states that
![]() $\Sigma _1$
-definable sets are Diophantine and it is a long standing open problem whether it is provable in
$\Sigma _1$
-definable sets are Diophantine and it is a long standing open problem whether it is provable in
![]() $I\Delta _0$
, i.e., Peano arithmetic with induction restricted to
$I\Delta _0$
, i.e., Peano arithmetic with induction restricted to
![]() $\Delta _0$
-formulas.
$\Delta _0$
-formulas.
Wilkie observed [Reference Wilkie36] that a positive answer would imply
![]() $\mathsf {NP}= \mathsf {co}\text {-}\mathsf {NP}$
. Gaifman and Dimitracopoulos [Reference Gaifman and Dimitracopoulos22] showed that adding exponentiation suffices:
$\mathsf {NP}= \mathsf {co}\text {-}\mathsf {NP}$
. Gaifman and Dimitracopoulos [Reference Gaifman and Dimitracopoulos22] showed that adding exponentiation suffices:
![]() $I\Delta _0+ \forall x\exists y\ 2^x{=}y$
does prove MRDP. Kaye [Reference Kaye27] proved MRDP using only induction for bounded existential formulas plus an axiom stating the totality of a suitable function of exponential growth. It is asked in [Reference Gaifman and Dimitracopoulos22, page 188] whether
$I\Delta _0+ \forall x\exists y\ 2^x{=}y$
does prove MRDP. Kaye [Reference Kaye27] proved MRDP using only induction for bounded existential formulas plus an axiom stating the totality of a suitable function of exponential growth. It is asked in [Reference Gaifman and Dimitracopoulos22, page 188] whether
![]() $I\Delta _0$
plus the totality of
$I\Delta _0$
plus the totality of
![]() $x^{\log x}$
, or of
$x^{\log x}$
, or of
![]() $x^{\log \log x}$
etc. proves MRDP. A positive answer would imply that
$x^{\log \log x}$
etc. proves MRDP. A positive answer would imply that
![]() $I\Delta _0$
proves MRDP for small numbers: this would mean that the equivalence of any
$I\Delta _0$
proves MRDP for small numbers: this would mean that the equivalence of any
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (\bar x)$
to some Diophantine formula is proved in
$\varphi (\bar x)$
to some Diophantine formula is proved in
![]() $I\Delta _0$
for all
$I\Delta _0$
for all
![]() $\bar x$
of logarithmic order. Model-theoretically, the equivalence holds in any
$\bar x$
of logarithmic order. Model-theoretically, the equivalence holds in any
![]() $I\Delta _0$
-model for all
$I\Delta _0$
-model for all
![]() $\bar x$
from the initial segment of numbers x such that
$\bar x$
from the initial segment of numbers x such that
![]() $2^x$
exists, while proof-theoretically, we allow an
$2^x$
exists, while proof-theoretically, we allow an
![]() $I\Delta _0$
-proof to use exponentiation, but only once. Such limited use of exponentiation has been studied in bounded arithmetic [Reference Krajíček29].
$I\Delta _0$
-proof to use exponentiation, but only once. Such limited use of exponentiation has been studied in bounded arithmetic [Reference Krajíček29].
We show that Theorem 1.3 implies:
Theorem 1.5. If
![]() $I\Delta _0$
proves MRDP for small numbers, then
$I\Delta _0$
proves MRDP for small numbers, then
![]() $\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
$\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
1.5
 $\mathsf {AC}^0$
-bi-immunity
$\mathsf {AC}^0$
-bi-immunity
Could Conjecture 1.1 be false? We give further evidence for its truth by establishing a connection to the existence of
![]() $\mathsf {AC}^0$
-bi-immune sets in
$\mathsf {AC}^0$
-bi-immune sets in
![]() $\mathsf {NP}$
. Recall a problem Q is
$\mathsf {NP}$
. Recall a problem Q is
![]() $\mathsf {AC}^0$
-immune if it does not have an infinite subset in
$\mathsf {AC}^0$
-immune if it does not have an infinite subset in
![]() $\mathsf {AC}^0$
; if additionally, also the complement of Q is
$\mathsf {AC}^0$
; if additionally, also the complement of Q is
![]() $\mathsf {AC}^0$
-immune, then Q is
$\mathsf {AC}^0$
-immune, then Q is
![]() $\mathsf {AC}^0$
-bi-immune.
$\mathsf {AC}^0$
-bi-immune.
Theorem 1.6. If
![]() $\mathsf {NP}$
contains an
$\mathsf {NP}$
contains an
![]() $\mathsf {AC}^0$
-bi-immune problem, then
$\mathsf {AC}^0$
-bi-immune problem, then ![]() .
.
It is a standard hypothesis that
![]() $\mathsf {NP}$
contains even
$\mathsf {NP}$
contains even
![]() $\mathsf {P}$
-bi-immune problems and this follows from the measure hypothesis [Reference Mayordomo31]. Whether
$\mathsf {P}$
-bi-immune problems and this follows from the measure hypothesis [Reference Mayordomo31]. Whether
![]() $\mathsf {NP}$
contains at least
$\mathsf {NP}$
contains at least
![]() $\mathsf {AC}^0$
-bi-immune problems has been asked once it was realized [Reference Allender, Beigel, Hertrampf and Homer1, Reference Geske, Huynh and Seiferas23] that deterministic time hierarchy theorems hold with bi-immunity (or, equivalently [Reference Balcázar and Schöning5], almost everywhere) while this is open for nondeterministic time [Reference Allender, Beigel, Hertrampf and Homer1, Reference Fortnow and Santhanam21]. While Zimand [Reference Zimand37] obtained some partial positive answers, Allender and Gore [Reference Allender, Gore and Cai2] showed that this has different answers relative to different oracles.Footnote
3
This indicates that also refuting Conjecture 1.1 might be non-trivial.
$\mathsf {AC}^0$
-bi-immune problems has been asked once it was realized [Reference Allender, Beigel, Hertrampf and Homer1, Reference Geske, Huynh and Seiferas23] that deterministic time hierarchy theorems hold with bi-immunity (or, equivalently [Reference Balcázar and Schöning5], almost everywhere) while this is open for nondeterministic time [Reference Allender, Beigel, Hertrampf and Homer1, Reference Fortnow and Santhanam21]. While Zimand [Reference Zimand37] obtained some partial positive answers, Allender and Gore [Reference Allender, Gore and Cai2] showed that this has different answers relative to different oracles.Footnote
3
This indicates that also refuting Conjecture 1.1 might be non-trivial.
1.6 Outline
Much of the technical work consists in connecting the dots between results of various subareas of logic and complexity, namely classical, parameterized and descriptive complexity theory and formal arithmetic. Section 2 reviews the results we need and fixes our notation. The technicalities are somewhat subtle, in particular, the move from ![]() to
to ![]() is crucial. Section 3 introduces almost tally problems and proves Theorem 1.2 and various variants of it. Section 4 proves Theorem 1.4. This together with the results in Section 3 implies Theorem 1.3 and various variants. Section 5 derives (a strengthening of) Theorem 1.5. Section 6 proves Theorem 1.6. The final section discusses the role of uniformity, and exhibits the different behaviours of our parameterized problems
is crucial. Section 3 introduces almost tally problems and proves Theorem 1.2 and various variants of it. Section 4 proves Theorem 1.4. This together with the results in Section 3 implies Theorem 1.3 and various variants. Section 5 derives (a strengthening of) Theorem 1.5. Section 6 proves Theorem 1.6. The final section discusses the role of uniformity, and exhibits the different behaviours of our parameterized problems ![]() ,
, ![]() and
and ![]() .
.
2 Preliminaries
Standard monographs are [Reference Arora and Barak3, Reference Papadimitriou32] for classical complexity theory, [Reference Downey and Fellows15, Reference Downey and Fellows16, Reference Flum and Grohe20] for parameterized complexity theory, [Reference Hájek and Pudlák25, Reference Kaye28] for formal arithmetic, and [Reference Ebbinghaus and Flum17, Reference Immerman26] for descriptive complexity theory.
2.1 Classical complexity
A (classical) problem is a subset of
![]() $\{0,1\}^*$
, the set of finite binary strings. The length of a binary string
$\{0,1\}^*$
, the set of finite binary strings. The length of a binary string
![]() $x\in \{0,1\}^*$
is denoted
$x\in \{0,1\}^*$
is denoted
![]() $|x|$
. For
$|x|$
. For
![]() $n\in \mathbb {N}$
we let
$n\in \mathbb {N}$
we let
![]() $1^n$
denote the binary string consisting of n many
$1^n$
denote the binary string consisting of n many
![]() $1$
’s. We use multitape Turing machines with alphabet
$1$
’s. We use multitape Turing machines with alphabet
![]() $\{0,1\}$
as our basic model of computation. When considering dlogtime Turing machines, i.e., deterministic machines running in time
$\{0,1\}$
as our basic model of computation. When considering dlogtime Turing machines, i.e., deterministic machines running in time
![]() $O(\log n)$
, it is understood that they access their input via an address tape (see, e.g., [Reference Barrington, Immerman and Straubing6]). As usual,
$O(\log n)$
, it is understood that they access their input via an address tape (see, e.g., [Reference Barrington, Immerman and Straubing6]). As usual,
![]() $\mathsf {P}$
and
$\mathsf {P}$
and
![]() $\mathsf {NP}$
denote deterministic and nondeterministic polynomial time
$\mathsf {NP}$
denote deterministic and nondeterministic polynomial time
![]() $n^{O(1)}$
, and
$n^{O(1)}$
, and
![]() $\mathsf {E}$
and
$\mathsf {E}$
and
![]() $\mathsf {NE}$
denote deterministic and nondeterministic exponential time with linear exponent
$\mathsf {NE}$
denote deterministic and nondeterministic exponential time with linear exponent
![]() $2^{O(n)}$
. The linear time hierarchy
$2^{O(n)}$
. The linear time hierarchy
![]() $\mathsf {LINH}$
is the set of problems acceptable by alternating Turing machines in linear time
$\mathsf {LINH}$
is the set of problems acceptable by alternating Turing machines in linear time
![]() $O(n)$
with
$O(n)$
with
![]() $O(1)$
alternations.
$O(1)$
alternations.
![]() $\mathsf {LINSPACE}$
and
$\mathsf {LINSPACE}$
and
![]() $\mathsf {NLINSPACE}$
denote deterministic and nondeterministic linear space
$\mathsf {NLINSPACE}$
denote deterministic and nondeterministic linear space
![]() $O(n)$
. Clearly,
$O(n)$
. Clearly,
Following [Reference Barrington, Immerman and Straubing6] we define (dlogtime uniform)
![]() $\mathsf {AC}^0$
as the set of problems decided by
$\mathsf {AC}^0$
as the set of problems decided by
![]() $\mathsf {AC}^0$
-circuit families
$\mathsf {AC}^0$
-circuit families
![]() $(\mathsf C_n)_{n\in \mathbb {N}}$
:
$(\mathsf C_n)_{n\in \mathbb {N}}$
:
-
–
 $\mathsf C_n$
is a circuit (with
$\mathsf C_n$
is a circuit (with
 $\wedge , \vee , \neg $
gates and unbounded fan-in) with n variables, size
$\wedge , \vee , \neg $
gates and unbounded fan-in) with n variables, size
 $\leqslant n^c$
and depthFootnote
4
$\leqslant n^c$
and depthFootnote
4
 $\leqslant d$
, where
$\leqslant d$
, where
 $c,d\in \mathbb {N}$
are two constants independent of n;
$c,d\in \mathbb {N}$
are two constants independent of n; -
– there is a dlogtime Turing machine which given
 $ \langle 1^n, i, b \rangle $
where
$ \langle 1^n, i, b \rangle $
where
 $n,i\in \mathbb {N}$
and
$n,i\in \mathbb {N}$
and
 $b\in \{0,1\}$
decides whether the ith bit of the binary encoding of
$b\in \{0,1\}$
decides whether the ith bit of the binary encoding of
 $\mathsf C_n$
is b.
$\mathsf C_n$
is b.
Here, for binary strings
![]() $x= x_0\dots x_{|x|-1}$
and
$x= x_0\dots x_{|x|-1}$
and
![]() $y= y_0\dots y_{|y|-1}$
we use the standard pairing
$y= y_0\dots y_{|y|-1}$
we use the standard pairing
and similarly for more arguments. The above definition is somewhat sensitive to the choice of the binary encoding of a circuit. An appropriate choice would be to encode
![]() $C_n$
by the list of strings in the direct connection language corresponding to n; we refer to [Reference Barrington, Immerman and Straubing6] for details.
$C_n$
by the list of strings in the direct connection language corresponding to n; we refer to [Reference Barrington, Immerman and Straubing6] for details.
For
![]() $n\in \mathbb {N}$
we let
$n\in \mathbb {N}$
we let
![]() $\mathit {bin}(n)\in \{0,1\}^*$
denote the binary expansion of n; it has length
$\mathit {bin}(n)\in \{0,1\}^*$
denote the binary expansion of n; it has length
![]() $\left \lceil \log (n+1)\right \rceil $
for
$\left \lceil \log (n+1)\right \rceil $
for
![]() $n>0$
. For
$n>0$
. For
![]() $x\in \{0,1\}^*$
let
$x\in \{0,1\}^*$
let
![]() $\mathit {num}(x)$
be the natural number with binary expansion
$\mathit {num}(x)$
be the natural number with binary expansion
![]() $1x$
, i.e.,
$1x$
, i.e.,
![]() $\mathit {bin}(\mathit {num}(x))= 1x$
. For a problem Q let
$\mathit {bin}(\mathit {num}(x))= 1x$
. For a problem Q let
The last statement of the following is [Reference Allender, Gore and Cai2, Proposition 5], and the first two are trivial:
Proposition 2.1 [Reference Allender, Gore and Cai2].
Let Q be a problem. Then:
-
(i)
 $Q\in \mathsf {NE}$
if and only if
$Q\in \mathsf {NE}$
if and only if
 $\mathit {un}(Q)\in \mathsf {NP}$
.
$\mathit {un}(Q)\in \mathsf {NP}$
. -
(ii)
 $Q\in \mathsf {E}$
if and only if
$Q\in \mathsf {E}$
if and only if
 $\mathit {un}(Q)\in \mathsf {P}$
.
$\mathit {un}(Q)\in \mathsf {P}$
. -
(iii)
 $Q\in \mathsf {LINH}$
if and only if
$Q\in \mathsf {LINH}$
if and only if
 $\mathit {un}(Q)\in \mathsf {AC}^0$
.
$\mathit {un}(Q)\in \mathsf {AC}^0$
.
2.2 Parameterized complexity
A parameterized problem is a pair
![]() $(Q, \kappa )$
of an underlying classical problem
$(Q, \kappa )$
of an underlying classical problem
![]() $Q\subseteq \{0,1\}^*$
and a parameterization
$Q\subseteq \{0,1\}^*$
and a parameterization
![]() $\kappa :\{0,1\}^*\to \mathbb {N}$
mapping an instance
$\kappa :\{0,1\}^*\to \mathbb {N}$
mapping an instance
![]() $x\in \{0,1\}^*$
to its parameter
$x\in \{0,1\}^*$
to its parameter
![]() $\kappa (x)\in \mathbb {N}$
. We follow [Reference Elberfeld, Stockhusen and Tantau18] and require that
$\kappa (x)\in \mathbb {N}$
. We follow [Reference Elberfeld, Stockhusen and Tantau18] and require that
![]() $\kappa $
is computable by an
$\kappa $
is computable by an
![]() $\mathsf {AC}^0$
-circuit family
$\mathsf {AC}^0$
-circuit family
![]() $(\mathsf C_n)_{n\in \mathbb {N}}$
. That is, for all
$(\mathsf C_n)_{n\in \mathbb {N}}$
. That is, for all
![]() ${x\in \{0,1\}^*}$
, besides
${x\in \{0,1\}^*}$
, besides
![]() $|x|$
inputs the circuit
$|x|$
inputs the circuit
![]() $C_{|x|}$
has
$C_{|x|}$
has
![]() $|x|$
outputs and computes
$|x|$
outputs and computes
![]() $\mathit {bin}(\kappa (x))$
, possibly padded with leading 0’s to length
$\mathit {bin}(\kappa (x))$
, possibly padded with leading 0’s to length
![]() $|x|$
. It is a technical assumption satisfied by almost all parameterized problems of interest. For example,
$|x|$
. It is a technical assumption satisfied by almost all parameterized problems of interest. For example, ![]() has underlying classical problem
has underlying classical problem
![]() $\big \{ \langle 1^n, \mathbb M \rangle \;\big |\;$
the nondeterministic Turing machine
$\big \{ \langle 1^n, \mathbb M \rangle \;\big |\;$
the nondeterministic Turing machine
![]() $\mathbb M$
accepts the empty input in at most n steps
$\mathbb M$
accepts the empty input in at most n steps
![]() $\big \}$
and a parameterization
$\big \}$
and a parameterization
![]() $\kappa $
that maps strings of the form
$\kappa $
that maps strings of the form
![]() $ \langle 1^n, \mathbb M \rangle $
to
$ \langle 1^n, \mathbb M \rangle $
to
![]() $|\mathbb M|$
and other strings to, say, 0.
$|\mathbb M|$
and other strings to, say, 0.
The para-operator [Reference Flum and Grohe19] turns a classical complexity class into a parameterized one (the most important intractable parameterized classes are not of this form, however). The class
![]() $\mathsf {para}\text {-}\mathsf {P}= \mathsf {FPT}$
contains the parameterized problems
$\mathsf {para}\text {-}\mathsf {P}= \mathsf {FPT}$
contains the parameterized problems
![]() $(Q,\kappa )$
that are fixed-parameter tractable, i.e., decidable in deterministic time
$(Q,\kappa )$
that are fixed-parameter tractable, i.e., decidable in deterministic time
![]() $f(\kappa (x))\cdot |x|^{O(1)}$
for some computable
$f(\kappa (x))\cdot |x|^{O(1)}$
for some computable
![]() $f:\mathbb {N}\to \mathbb {N}$
. Similarly,
$f:\mathbb {N}\to \mathbb {N}$
. Similarly,
![]() $\mathsf {para}\text {-}\mathsf {NP}$
denotes nondeterministic time
$\mathsf {para}\text {-}\mathsf {NP}$
denotes nondeterministic time
![]() $f(\kappa (x))\cdot |x|^{O(1)}$
(for any computable f),
$f(\kappa (x))\cdot |x|^{O(1)}$
(for any computable f),
![]() $\mathsf {para}\text {-}\mathsf {L}$
denotes deterministic space
$\mathsf {para}\text {-}\mathsf {L}$
denotes deterministic space
![]() $f(\kappa (x))+O(\log |x|)$
, and
$f(\kappa (x))+O(\log |x|)$
, and
![]() $\mathsf {para}\text {-}\mathsf {NL}$
denotes nondeterministic such space. Clearly,
$\mathsf {para}\text {-}\mathsf {NL}$
denotes nondeterministic such space. Clearly,
The central parameterized class in this paper is
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
. It is characterized as follows:
$\mathsf {para}\text {-}\mathsf {AC}^0$
. It is characterized as follows:
Proposition 2.2 [Reference Chen and Flum11].
Let
![]() $(Q, \kappa )$
be a parameterized problem. The following are equivalent:
$(Q, \kappa )$
be a parameterized problem. The following are equivalent:
-
(i)
 $(Q,\kappa )\in \mathsf {para}\text {-}\mathsf {AC}^0$
.
$(Q,\kappa )\in \mathsf {para}\text {-}\mathsf {AC}^0$
. -
(ii) There is a family
 $(\mathsf C_{n,k})_{n,k\in \mathbb {N}}$
of circuits such that:
$(\mathsf C_{n,k})_{n,k\in \mathbb {N}}$
of circuits such that:-
– there are a computable
 $f:\mathbb {N}\to \mathbb {N}$
and
$f:\mathbb {N}\to \mathbb {N}$
and
 $c,d\in \mathbb {N}$
such that for all
$c,d\in \mathbb {N}$
such that for all
 $n,k\in \mathbb {N}$
the circuit
$n,k\in \mathbb {N}$
the circuit
 $\mathsf C_{n,k}$
has n inputs, size at most
$\mathsf C_{n,k}$
has n inputs, size at most
 $ f(k)\cdot n^c$
, and depth at most d;
$ f(k)\cdot n^c$
, and depth at most d; -
– for all
 $x\in \{0,1\}^*$
we have
$x\in \{0,1\}^*$
we have  $$\begin{align*}x\in Q\iff \mathsf C_{|x|, \kappa(x)}(x)=1; \end{align*}$$
$$\begin{align*}x\in Q\iff \mathsf C_{|x|, \kappa(x)}(x)=1; \end{align*}$$
-
– there are a computable
 $g:\mathbb {N}\to \mathbb {N}$
and a deterministic Turing machine which given as input
$g:\mathbb {N}\to \mathbb {N}$
and a deterministic Turing machine which given as input
 $ \langle 1^n, 1^k, i, b \rangle $
where
$ \langle 1^n, 1^k, i, b \rangle $
where
 $n,k,i\in \mathbb {N}$
and
$n,k,i\in \mathbb {N}$
and
 $b\in \{0,1\}$
decides in time
$b\in \{0,1\}$
decides in time
 $g(k)+ O(\log n)$
whether the ith bit of the binary encoding of
$g(k)+ O(\log n)$
whether the ith bit of the binary encoding of
 $\mathsf C_{n,k}$
is b.
$\mathsf C_{n,k}$
is b.
-
-
(iii) Q is decidable and there are a computable
 $h: \mathbb {N}\to \mathbb {N}$
and an
$h: \mathbb {N}\to \mathbb {N}$
and an
 $\mathsf {AC}^0$
-circuit family
$\mathsf {AC}^0$
-circuit family
 $(\mathsf C_n)_{n\in \mathbb {N}}$
such that for all
$(\mathsf C_n)_{n\in \mathbb {N}}$
such that for all
 $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
 $|x|\geqslant h(\kappa (x))$
we have
$|x|\geqslant h(\kappa (x))$
we have  $$\begin{align*}x\in Q\iff \mathsf C_{|x|}(x)=1. \end{align*}$$
$$\begin{align*}x\in Q\iff \mathsf C_{|x|}(x)=1. \end{align*}$$
According to the terminology of [Reference Flum and Grohe19], (iii) states that
![]() $(Q,\kappa )$
is eventually in
$(Q,\kappa )$
is eventually in
![]() $\mathsf {AC}^0$
.
$\mathsf {AC}^0$
.
2.3 Formal arithmetic
We let
![]() $L_{\text {ar}}:= \{+,\times ,0,1,<\}$
be the language of arithmetic with binary function symbols
$L_{\text {ar}}:= \{+,\times ,0,1,<\}$
be the language of arithmetic with binary function symbols
![]() $+,\times $
, constants
$+,\times $
, constants
![]() $0,1$
and a binary relation symbol
$0,1$
and a binary relation symbol
![]() $<$
. The standard
$<$
. The standard
![]() $L_{\text {ar}}$
-structure, denoted
$L_{\text {ar}}$
-structure, denoted
![]() $\mathbb {N}$
, has universe
$\mathbb {N}$
, has universe
![]() $\mathbb {N}$
and interprets the symbols in the obvious way. Every
$\mathbb {N}$
and interprets the symbols in the obvious way. Every
![]() $L_{\text {ar}}$
-term p computes a polynomial with coefficients in
$L_{\text {ar}}$
-term p computes a polynomial with coefficients in
![]() $\mathbb {N}$
and of total degree at most
$\mathbb {N}$
and of total degree at most
![]() $|p|$
. We do not distinguish terms p or formulas
$|p|$
. We do not distinguish terms p or formulas
![]() $\varphi $
from their binary encodings, so
$\varphi $
from their binary encodings, so
![]() $|p|$
and
$|p|$
and
![]() $|\varphi |$
denote the lengths of these encodings. Writing
$|\varphi |$
denote the lengths of these encodings. Writing
![]() $\varphi (\bar x)$
for a formula
$\varphi (\bar x)$
for a formula
![]() $\varphi $
means that all free variables of
$\varphi $
means that all free variables of
![]() $\varphi $
are among
$\varphi $
are among
![]() $\bar x$
. A sentence is a formula without free variables.
$\bar x$
. A sentence is a formula without free variables.
A
![]() $\Delta _0$
-formula is an
$\Delta _0$
-formula is an
![]() $L_{\text {ar}}$
-formula obtained from atomic formulas, Boolean connectives, and bounded quantifiers
$L_{\text {ar}}$
-formula obtained from atomic formulas, Boolean connectives, and bounded quantifiers
![]() $\exists x{<}p$
,
$\exists x{<}p$
,
![]() $\forall x{<}p$
where p is an
$\forall x{<}p$
where p is an
![]() $L_{\text {ar}}$
-term not involving x; e.g.,
$L_{\text {ar}}$
-term not involving x; e.g.,
![]() $\exists x{<}p\; \varphi $
stands for
$\exists x{<}p\; \varphi $
stands for
![]() $\exists x (x{<}p\wedge \varphi )$
.
$\exists x (x{<}p\wedge \varphi )$
.
![]() $\Sigma _1$
- and
$\Sigma _1$
- and
![]() $\Pi _1$
-formulas are obtained from
$\Pi _1$
-formulas are obtained from
![]() $\Delta _0$
-formulas by existential and universal quantification, respectively.
$\Delta _0$
-formulas by existential and universal quantification, respectively.
Theorem 2.3 (MRDP).
For every
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (\bar x)$
there are
$\varphi (\bar x)$
there are
![]() $L_{\text {ar}}$
-terms
$L_{\text {ar}}$
-terms
![]() $p(\bar x,\bar y),q(\bar x,\bar y)$
such that
$p(\bar x,\bar y),q(\bar x,\bar y)$
such that
Gödel showed that computable functions are
![]() $\Sigma _1$
-definable. The MRDP theorem improves this to an existential definition:
$\Sigma _1$
-definable. The MRDP theorem improves this to an existential definition:
Corollary 2.4. For every computable
![]() $f:\mathbb {N}\to \mathbb {N}$
there is a quantifier-free
$f:\mathbb {N}\to \mathbb {N}$
there is a quantifier-free
![]() $L_{\text {ar}}$
-formula
$L_{\text {ar}}$
-formula
![]() $\varphi _f(x, y, \bar z)$
such that for every
$\varphi _f(x, y, \bar z)$
such that for every
![]() $n,m\in \mathbb {N}$
$n,m\in \mathbb {N}$
We are mainly concerned with finite arithmetical structures with universe
for some
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n\geqslant 2$
, and therefore consider the relational version
$n\geqslant 2$
, and therefore consider the relational version
of
![]() $L_{\text {ar}}$
where
$L_{\text {ar}}$
where
![]() $+$
,
$+$
,
![]() $\times $
are ternary relation symbols. The standard
$\times $
are ternary relation symbols. The standard
![]() $L_{\text {ar}}^{\text {r}}$
-structure with universe
$L_{\text {ar}}^{\text {r}}$
-structure with universe
![]() $\mathbb {N}$
, also denoted
$\mathbb {N}$
, also denoted
![]() $\mathbb {N}$
, interprets
$\mathbb {N}$
, interprets
![]() $+$
,
$+$
,
![]() $\times $
by the graphs of addition and multiplication, respectively. For
$\times $
by the graphs of addition and multiplication, respectively. For
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n>1$
, the standard
$n>1$
, the standard
![]() $L^{\text {r}}_{\text {ar}}$
-structure with universe
$L^{\text {r}}_{\text {ar}}$
-structure with universe
![]() $[n]$
, simply denoted n, is the substructure of
$[n]$
, simply denoted n, is the substructure of
![]() $\mathbb {N}$
with universe
$\mathbb {N}$
with universe
![]() $[n]$
, i.e., it interprets the symbols in
$[n]$
, i.e., it interprets the symbols in
![]() $L^{\text {r}}_{\text {ar}}$
by
$L^{\text {r}}_{\text {ar}}$
by
![]() $+^{[n]}:= \{(k,\ell ,m) \in [n]^3\mid k+\ell =m\}$
,
$+^{[n]}:= \{(k,\ell ,m) \in [n]^3\mid k+\ell =m\}$
,
![]() $\times ^{[n]}:= \{(k,\ell ,m)\in [n]^3\mid k\cdot \ell = m\}$
,
$\times ^{[n]}:= \{(k,\ell ,m)\in [n]^3\mid k\cdot \ell = m\}$
,
![]() $0^{[n]}:= 0$
,
$0^{[n]}:= 0$
,
![]() $1^{[n]}:= 1$
and
$1^{[n]}:= 1$
and
![]() $<^{[n]}:= \{(k,\ell )\in [n]^2\mid k< \ell \}$
.
$<^{[n]}:= \{(k,\ell )\in [n]^2\mid k< \ell \}$
.
Let
![]() $\varphi ^{<y}$
be obtained from
$\varphi ^{<y}$
be obtained from
![]() $\varphi $
by replacing all quantifiers
$\varphi $
by replacing all quantifiers
![]() $\exists z$
,
$\exists z$
,
![]() $\forall z$
by
$\forall z$
by
![]() $\exists z{<}y$
,
$\exists z{<}y$
,
![]() $\forall z{<}y$
. For
$\forall z{<}y$
. For
![]() $\bar n=(n_0,\ldots , n_{k-1})\in \mathbb {N}^k$
and
$\bar n=(n_0,\ldots , n_{k-1})\in \mathbb {N}^k$
and
![]() $n\in \mathbb {N}$
write
$n\in \mathbb {N}$
write
![]() $\bar n<n$
to express
$\bar n<n$
to express
![]() $n_i<n$
for all
$n_i<n$
for all
![]() $i<k$
. For every
$i<k$
. For every
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\varphi (\bar x)$
with
$\varphi (\bar x)$
with
![]() $1, \bar n<n$
we have
$1, \bar n<n$
we have
Remark 2.5. Corollary 2.4 holds for a quantifier-free
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\varphi _f(\bar x, y, \bar z)$
. Indeed, it is straightforward to express an
$\varphi _f(\bar x, y, \bar z)$
. Indeed, it is straightforward to express an
![]() $L_{\text {ar}}$
-term (in)equality by an existential
$L_{\text {ar}}$
-term (in)equality by an existential
![]() $L^{\text {r}}_{\text {ar}}$
-formula.
$L^{\text {r}}_{\text {ar}}$
-formula.
2.4 Descriptive complexity
A binary string
![]() $x= x_0\cdots x_{n-1}\in \{0,1\}^*$
of length
$x= x_0\cdots x_{n-1}\in \{0,1\}^*$
of length
![]() $n>1$
is often identified with the string structure
$n>1$
is often identified with the string structure
![]() ${\mathcal S}(x)$
defined as the
${\mathcal S}(x)$
defined as the
![]() $L^{\text {r}}_{\text {ar}}\cup \{\mathit {ONE}\}$
-expansion of the standard
$L^{\text {r}}_{\text {ar}}\cup \{\mathit {ONE}\}$
-expansion of the standard
![]() $L^{\text {r}}_{\text {ar}}$
-structure n that interprets the unary relation symbol
$L^{\text {r}}_{\text {ar}}$
-structure n that interprets the unary relation symbol
![]() $\mathit {ONE}$
by
$\mathit {ONE}$
by
i.e.,
![]() ${\mathcal S}(x)= \big ([n], +^{[n]}, \times ^{[n]}, 0^{[n]}, 1^{[n]}, <^{[n]}, \mathit {ONE}^x\big )$
. We shall work with the following descriptive characterization of (dlogtime uniform)
${\mathcal S}(x)= \big ([n], +^{[n]}, \times ^{[n]}, 0^{[n]}, 1^{[n]}, <^{[n]}, \mathit {ONE}^x\big )$
. We shall work with the following descriptive characterization of (dlogtime uniform)
![]() $\mathsf {AC}^0$
:
$\mathsf {AC}^0$
:
Theorem 2.6 [Reference Barrington, Immerman and Straubing6].
A problem Q is in
![]() $\mathsf {AC}^0$
if and only if there is an
$\mathsf {AC}^0$
if and only if there is an
![]() $L^{\text {r}}_{\text {ar}}\cup \{\mathit {ONE}\}$
-sentence
$L^{\text {r}}_{\text {ar}}\cup \{\mathit {ONE}\}$
-sentence
![]() $\varphi $
such that for every
$\varphi $
such that for every
![]() $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
![]() $|x|\geqslant 2$
:
$|x|\geqslant 2$
:
This result and Proposition 2.2(iii) imply what is to be our working definition of
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
: the parameterized problems that are eventually definable.
$\mathsf {para}\text {-}\mathsf {AC}^0$
: the parameterized problems that are eventually definable.
Corollary 2.7. Let
![]() $(Q, \kappa )$
be a parameterized problem with decidable Q. Then
$(Q, \kappa )$
be a parameterized problem with decidable Q. Then
![]() $(Q, \kappa )$
is in
$(Q, \kappa )$
is in
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
if and only if
$\mathsf {para}\text {-}\mathsf {AC}^0$
if and only if
![]() $(Q, \kappa )$
is eventually definable: there are a computable
$(Q, \kappa )$
is eventually definable: there are a computable
![]() $h: \mathbb {N}\to \mathbb {N}$
and an
$h: \mathbb {N}\to \mathbb {N}$
and an
![]() $L^{\text {r}}_{\text {ar}}\cup \{\mathit {ONE}\}$
-sentence
$L^{\text {r}}_{\text {ar}}\cup \{\mathit {ONE}\}$
-sentence
![]() $\varphi $
such that for all
$\varphi $
such that for all
![]() $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
![]() $|x|\geqslant h(\kappa (x))$
:
$|x|\geqslant h(\kappa (x))$
:
In descriptive complexity the role of reductions is played by interpretations. Let
![]() $L,L'$
be languages consisting of relation symbols and constants. Let
$L,L'$
be languages consisting of relation symbols and constants. Let
![]() $w\in \mathbb {N}$
with
$w\in \mathbb {N}$
with
![]() $w\geqslant 1$
. An interpretation
$w\geqslant 1$
. An interpretation
![]() ${\mathit I}$
of
${\mathit I}$
of
![]() $L'$
in L (of width w) is given by an L-formula
$L'$
in L (of width w) is given by an L-formula
![]() $\varphi _{\text {uni}}(\bar x)$
, an L-formula
$\varphi _{\text {uni}}(\bar x)$
, an L-formula
![]() $\varphi _R(\bar x_0, \dots , \bar x_{r-1})$
for each r-ary relation symbol
$\varphi _R(\bar x_0, \dots , \bar x_{r-1})$
for each r-ary relation symbol
![]() $R\in L'$
, and an L-formula
$R\in L'$
, and an L-formula
![]() $\varphi _c(\bar x)$
for every constant
$\varphi _c(\bar x)$
for every constant
![]() $c\in L'$
; here,
$c\in L'$
; here,
![]() $\bar x$
,
$\bar x$
,
![]() $\bar x_i$
are w-tuples of variables. Given an L-structure A define the
$\bar x_i$
are w-tuples of variables. Given an L-structure A define the
![]() $L'$
-structure
$L'$
-structure
![]() $A^{{\mathit I}}$
as follows. It has universe
$A^{{\mathit I}}$
as follows. It has universe
![]() $A^{{\mathit I}}:= \big \{\bar a\in A^w\;\big |\; A\models \varphi _{\text {uni}}(\bar a)\big \}$
, interprets an r-ary
$A^{{\mathit I}}:= \big \{\bar a\in A^w\;\big |\; A\models \varphi _{\text {uni}}(\bar a)\big \}$
, interprets an r-ary
![]() $R\in L'$
by
$R\in L'$
by
![]() $\big \{(\bar a_0,\ldots ,\bar a_{r-1})\in (A^{{\mathit I}})^r \;\big |\; A\models \varphi _R(\bar a_0, \ldots , \bar a_{r-1}) \big \}$
, and a constant
$\big \{(\bar a_0,\ldots ,\bar a_{r-1})\in (A^{{\mathit I}})^r \;\big |\; A\models \varphi _R(\bar a_0, \ldots , \bar a_{r-1}) \big \}$
, and a constant
![]() $c\in L'$
by the unique
$c\in L'$
by the unique
![]() $\bar a\in A^{{\mathit I}}$
satisfying
$\bar a\in A^{{\mathit I}}$
satisfying
![]() $\varphi _c(\bar x)$
in A. If this uniqueness is violated or if the universe
$\varphi _c(\bar x)$
in A. If this uniqueness is violated or if the universe
![]() $A^{{\mathit I}}$
is empty, then
$A^{{\mathit I}}$
is empty, then
![]() $A^{{\mathit I}}$
is not defined. If
$A^{{\mathit I}}$
is not defined. If
![]() $B\cong A^I$
for some I, we say B is interpretable in A. The following is standard.
$B\cong A^I$
for some I, we say B is interpretable in A. The following is standard.
Lemma 2.8. Let
![]() ${\mathit I} $
an interpretation of
${\mathit I} $
an interpretation of
![]() $L'$
in L of width w and
$L'$
in L of width w and
![]() $I'$
an interpretation of
$I'$
an interpretation of
![]() $L"$
in
$L"$
in
![]() $L'$
of width
$L'$
of width
![]() $w'$
. Further let A be an L-structure such that
$w'$
. Further let A be an L-structure such that
![]() $A^I$
is defined.
$A^I$
is defined.
-
(i) For every
 $L'$
-formula
$L'$
-formula
 $\varphi (x,y,\ldots )$
there is an L-formula
$\varphi (x,y,\ldots )$
there is an L-formula
 $\varphi ^I(\bar x,\bar y,\ldots )$
where
$\varphi ^I(\bar x,\bar y,\ldots )$
where
 $\bar x, \bar y, \ldots $
are w-tuples of variables such that for all
$\bar x, \bar y, \ldots $
are w-tuples of variables such that for all
 $\bar a, \bar b, \ldots \in A^I$
:
$\bar a, \bar b, \ldots \in A^I$
:  $$ \begin{align*} A^I \models \varphi(\bar a, \bar b, \ldots) & \iff A \models \varphi^I(\bar a, \bar b, \ldots). \end{align*} $$
$$ \begin{align*} A^I \models \varphi(\bar a, \bar b, \ldots) & \iff A \models \varphi^I(\bar a, \bar b, \ldots). \end{align*} $$
-
(ii) There is an interpretation
 $I'\circ I$
of
$I'\circ I$
of
 $L"$
in L of width
$L"$
in L of width
 $w\cdot w'$
such that if
$w\cdot w'$
such that if
 $(A^I)^{I'}$
is defined, then so is
$(A^I)^{I'}$
is defined, then so is
 $A^{I'\circ I}$
and
$A^{I'\circ I}$
and  $$\begin{align*}A^{I'\circ I }\cong (A^I)^{I'}. \end{align*}$$
$$\begin{align*}A^{I'\circ I }\cong (A^I)^{I'}. \end{align*}$$
The following is folklore, and a proof can be found in [Reference Schweikardt35, Appendix].
Lemma 2.9. Let
![]() $d\in \mathbb {N}$
.
$d\in \mathbb {N}$
.
-
(i) For every
 $n>1$
the standard
$n>1$
the standard
 $L^{\text {r}}_{\text {ar}}$
-structure
$L^{\text {r}}_{\text {ar}}$
-structure
 $n^d$
is interpretable in the standard
$n^d$
is interpretable in the standard
 $L^{\text {r}}_{\text {ar}}$
-structure n. In fact, there is an interpretation
$L^{\text {r}}_{\text {ar}}$
-structure n. In fact, there is an interpretation
 ${\mathit I} _d$
of width d such that
${\mathit I} _d$
of width d such that
 $n^d\cong n^{I_d}$
for every
$n^d\cong n^{I_d}$
for every
 $n>1$
, and the isomorphism maps each
$n>1$
, and the isomorphism maps each
 $a<n^d$
to the length d representation of a in base n.
$a<n^d$
to the length d representation of a in base n. -
(ii) There is an
 $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
 $\mathit {BIT}(x, y)$
such that for every
$\mathit {BIT}(x, y)$
such that for every
 $n>1$
and all
$n>1$
and all
 $i, j\in [n]$
:
$i, j\in [n]$
:  $$ \begin{align*} n\models \mathit{BIT}(i,j) & \iff \text{the } j\text{th bit of } \mathit{bin}(i) \text{ is } 1. \end{align*} $$
$$ \begin{align*} n\models \mathit{BIT}(i,j) & \iff \text{the } j\text{th bit of } \mathit{bin}(i) \text{ is } 1. \end{align*} $$
3
 and
and
 $\mathsf {NE}$
versus
$\mathsf {NE}$
versus
 $\mathsf {LINH}$
$\mathsf {LINH}$
In this section we first introduce a workable notion of reduction that preserves
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
, then prove Theorem 1.2, then introduce almost tally problems and show
$\mathsf {para}\text {-}\mathsf {AC}^0$
, then prove Theorem 1.2, then introduce almost tally problems and show ![]() is the hardest among them in
is the hardest among them in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
, and finally consider some generalizations and variants that will be instrumental later in Section 4 for the proof of Theorem 1.3 and its variants.
$\mathsf {para}\text {-}\mathsf {NP}$
, and finally consider some generalizations and variants that will be instrumental later in Section 4 for the proof of Theorem 1.3 and its variants.
3.1 Eventually definable reductions
A parameterized reduction from a parameterized problem
![]() $(Q,\kappa )$
to another
$(Q,\kappa )$
to another
![]() $(Q',\kappa ')$
is a reduction
$(Q',\kappa ')$
is a reduction
![]() $r:\{0,1\}^*\to \{0,1\}^*$
from Q to
$r:\{0,1\}^*\to \{0,1\}^*$
from Q to
![]() $Q'$
such that
$Q'$
such that
![]() $\kappa '\circ r\leqslant f\circ \kappa $
for some computable function
$\kappa '\circ r\leqslant f\circ \kappa $
for some computable function
![]() $f: \mathbb {N}\to \mathbb {N}$
.
$f: \mathbb {N}\to \mathbb {N}$
.
Definition 3.1. Let
![]() $\kappa $
be a parameterization. A function
$\kappa $
be a parameterization. A function
![]() $r: \{0,1\}^*\to \{0,1\}^*$
is
$r: \{0,1\}^*\to \{0,1\}^*$
is
![]() $\kappa $
-eventually definable if there are a computable
$\kappa $
-eventually definable if there are a computable
![]() $h: \mathbb {N} \to \mathbb {N}$
and an interpretation
$h: \mathbb {N} \to \mathbb {N}$
and an interpretation
![]() ${\mathit I} $
such that
${\mathit I} $
such that
for all
![]() $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
![]() $|x|\geqslant h(\kappa (x))$
.
$|x|\geqslant h(\kappa (x))$
.
Example 3.2. The function
where
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $x\in \{0,1\}^*$
is
$x\in \{0,1\}^*$
is
![]() $\kappa $
-eventually definable where
$\kappa $
-eventually definable where
![]() $\kappa $
maps
$\kappa $
maps
![]() $ \langle 1^n, x \rangle $
to
$ \langle 1^n, x \rangle $
to
![]() $|x|$
(both functions map arguments that are not of the required form to, say,
$|x|$
(both functions map arguments that are not of the required form to, say,
![]() $0$
).
$0$
).
Proof Note
![]() $\mathit {num}( \langle \mathit {bin}(n), x \rangle )< 2^{| \langle \mathit {bin}(n), x \rangle |+ 1}\leqslant 2^{O(\log n+ |x|)}$
. Choose a constant
$\mathit {num}( \langle \mathit {bin}(n), x \rangle )< 2^{| \langle \mathit {bin}(n), x \rangle |+ 1}\leqslant 2^{O(\log n+ |x|)}$
. Choose a constant
![]() $d\in \mathbb {N}$
and a computable
$d\in \mathbb {N}$
and a computable
![]() $h: \mathbb {N} \to \mathbb {N}$
such that
$h: \mathbb {N} \to \mathbb {N}$
such that
![]() $\mathit {num}( \langle \mathit {bin}(n), x \rangle )< n^d$
and
$\mathit {num}( \langle \mathit {bin}(n), x \rangle )< n^d$
and
![]() $\mathit {num}(x)< n$
whenever
$\mathit {num}(x)< n$
whenever
![]() $n\geqslant h(|x|)$
. It suffices to describe an interpretation of
$n\geqslant h(|x|)$
. It suffices to describe an interpretation of
![]() ${\mathcal S}(1^{\mathit {num}( \langle \mathit {bin}(n), x \rangle )})$
in
${\mathcal S}(1^{\mathit {num}( \langle \mathit {bin}(n), x \rangle )})$
in
![]() ${\mathcal S}( \langle 1^n, x \rangle )$
whenever
${\mathcal S}( \langle 1^n, x \rangle )$
whenever
![]() $n\geqslant h(|x|)$
. It will be clear that the interpretation does not depend on n, x.
$n\geqslant h(|x|)$
. It will be clear that the interpretation does not depend on n, x.
Let
![]() $(n,\mathit {num}(x))$
be the expansion of the standard
$(n,\mathit {num}(x))$
be the expansion of the standard
![]() $L^{\text {r}}_{\text {ar}}$
-structure n that interprets a new constant by
$L^{\text {r}}_{\text {ar}}$
-structure n that interprets a new constant by
![]() $\mathit {num}(x)\in [n]$
. This is interpretable in
$\mathit {num}(x)\in [n]$
. This is interpretable in
![]() ${\mathcal S}( \langle 1^n, x \rangle )$
using
${\mathcal S}( \langle 1^n, x \rangle )$
using
![]() $\mathit {BIT}$
. By Lemma 2.9, also
$\mathit {BIT}$
. By Lemma 2.9, also
![]() $(n^d, \mathit {num}(x))$
is interpretable in
$(n^d, \mathit {num}(x))$
is interpretable in
![]() ${\mathcal S}( \langle 1^n, x \rangle )$
. But this structure defines (n and)
${\mathcal S}( \langle 1^n, x \rangle )$
. But this structure defines (n and)
![]() $\mathit {num}( \langle \mathit {bin}(n), x \rangle )\in [n^d]$
using
$\mathit {num}( \langle \mathit {bin}(n), x \rangle )\in [n^d]$
using
![]() $\mathit {BIT}$
. Thus,
$\mathit {BIT}$
. Thus,
![]() $\mathcal S(1^{\mathit {num}( \langle \mathit {bin}(n), x \rangle )})$
is interpretable in
$\mathcal S(1^{\mathit {num}( \langle \mathit {bin}(n), x \rangle )})$
is interpretable in
![]() ${\mathcal S}( \langle 1^n, x \rangle )$
as claimed.
${\mathcal S}( \langle 1^n, x \rangle )$
as claimed.
Finally, note there is a sentence
![]() $\varphi $
that is true exactly in structures of the desired form
$\varphi $
that is true exactly in structures of the desired form
![]() ${\mathcal S}( \langle 1^n,x \rangle )$
for
${\mathcal S}( \langle 1^n,x \rangle )$
for
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $x\in \{0,1\}^*$
. It is easy to modify the above interpretation to produce a structure isomorphic to
$x\in \{0,1\}^*$
. It is easy to modify the above interpretation to produce a structure isomorphic to
![]() ${\mathcal S}(0)$
given a structure that is not of the desired form.
${\mathcal S}(0)$
given a structure that is not of the desired form.
Example 3.3. Let
![]() $P:\{0,1\}^*\to \{0,1\}^*$
be computable. The function
$P:\{0,1\}^*\to \{0,1\}^*$
be computable. The function
where
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $x\in \{0,1\}^*$
is
$x\in \{0,1\}^*$
is
![]() $\kappa $
-eventually definable where
$\kappa $
-eventually definable where
![]() $\kappa $
maps
$\kappa $
maps
![]() $ \langle 1^n, x \rangle $
to
$ \langle 1^n, x \rangle $
to
![]() $|x|$
(both functions map arguments that are not of the required form to, say,
$|x|$
(both functions map arguments that are not of the required form to, say,
![]() $0$
).
$0$
).
Proof Let
![]() $p: \mathbb {N} \to \mathbb {N}$
be computable with
$p: \mathbb {N} \to \mathbb {N}$
be computable with
![]() $p(\mathit {num}(x))= \mathit {num}(P(x))$
for all
$p(\mathit {num}(x))= \mathit {num}(P(x))$
for all
![]() ${x\in \{0,1\}^*}$
. We choose:
${x\in \{0,1\}^*}$
. We choose:
-
• a quantifier-free
 $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
 $\varphi (x, y, \bar z)$
according to Remark 2.5,
$\varphi (x, y, \bar z)$
according to Remark 2.5, -
• a computable
 $f: \mathbb {N}\to \mathbb {N}$
so that for all
$f: \mathbb {N}\to \mathbb {N}$
so that for all
 $\ell \in \mathbb {N}$
$\ell \in \mathbb {N}$
 $$\begin{align*}\mathbb{N}\models \exists \bar z {<} f(\ell)\ \varphi(\ell,p(\ell),\bar z), \end{align*}$$
$$\begin{align*}\mathbb{N}\models \exists \bar z {<} f(\ell)\ \varphi(\ell,p(\ell),\bar z), \end{align*}$$
-
• and a computable
 $h{\kern-1pt}:{\kern-1pt} \mathbb {N}\to \mathbb {N}$
such that
$h{\kern-1pt}:{\kern-1pt} \mathbb {N}\to \mathbb {N}$
such that
 $h(|x|){\kern-1pt}>{\kern-1pt} \mathit {num}(x), \mathit {num}(P(x)), f(\mathit {num}(x))$
for all
$h(|x|){\kern-1pt}>{\kern-1pt} \mathit {num}(x), \mathit {num}(P(x)), f(\mathit {num}(x))$
for all
 $x\in \{0,1\}^*$
.
$x\in \{0,1\}^*$
.
Assume
![]() $n\geqslant h(|x|)$
. Then
$n\geqslant h(|x|)$
. Then
![]() ${\mathcal S}( \langle 1^n,x \rangle )$
interprets the expansion
${\mathcal S}( \langle 1^n,x \rangle )$
interprets the expansion
![]() $(n,\ell )$
of the standard structure n by a constant c interpreting
$(n,\ell )$
of the standard structure n by a constant c interpreting
![]() $\ell :=\mathit {num}(x)$
. In
$\ell :=\mathit {num}(x)$
. In
![]() $(n,\ell )$
the formula
$(n,\ell )$
the formula
![]() $\exists \bar z\varphi (c,y,\bar z)$
defines
$\exists \bar z\varphi (c,y,\bar z)$
defines
![]() $p(\ell )=\mathit {num}(P(x))$
. Using
$p(\ell )=\mathit {num}(P(x))$
. Using
![]() $\mathit {BIT}$
, thus
$\mathit {BIT}$
, thus
![]() ${\mathcal S}( \langle 1^n,x \rangle )$
interprets
${\mathcal S}( \langle 1^n,x \rangle )$
interprets
![]() ${\mathcal S}( \langle 1^n,P(x) \rangle )$
.
${\mathcal S}( \langle 1^n,P(x) \rangle )$
.
Again it is easy to modify this interpretation to produce a structure isomorphic to
![]() ${\mathcal S}(0)$
given a structure that is not of the desired form.
${\mathcal S}(0)$
given a structure that is not of the desired form.
Recall, a function
![]() $r:\{0,1\}^*\to \{0,1\}^*$
is honest if
$r:\{0,1\}^*\to \{0,1\}^*$
is honest if
![]() $|r(x)|\geqslant |x|^{\Omega (1)}$
.
$|r(x)|\geqslant |x|^{\Omega (1)}$
.
Lemma 3.4. Assume that
![]() $r,r': \{0,1\}^*\to \{0,1\}^*$
are
$r,r': \{0,1\}^*\to \{0,1\}^*$
are
![]() $\kappa $
- and
$\kappa $
- and
![]() $\kappa '$
-eventually definable, respectively, that
$\kappa '$
-eventually definable, respectively, that
![]() $\kappa '\circ r\leqslant f\circ \kappa $
for some computable
$\kappa '\circ r\leqslant f\circ \kappa $
for some computable
![]() $f:\mathbb {N}\to \mathbb {N}$
, and that r is honest. Then
$f:\mathbb {N}\to \mathbb {N}$
, and that r is honest. Then
![]() $r'\circ r$
is
$r'\circ r$
is
![]() $\kappa $
-eventually definable.
$\kappa $
-eventually definable.
Proof Choose
![]() ${\mathit I} , h$
for r and
${\mathit I} , h$
for r and
![]() ${\mathit I} ', h'$
for
${\mathit I} ', h'$
for
![]() $r'$
according to Definition 3.1. We can assume that
$r'$
according to Definition 3.1. We can assume that
![]() $h'$
is nondecreasing. Choose
$h'$
is nondecreasing. Choose
![]() $n_0, c\in \mathbb {N}$
such that
$n_0, c\in \mathbb {N}$
such that
![]() $|r(x)|\geqslant |x|^{1/c}$
for all
$|r(x)|\geqslant |x|^{1/c}$
for all
![]() $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
![]() $|x|\geqslant n_0$
. Define
$|x|\geqslant n_0$
. Define
![]() $g: \mathbb {N}\to \mathbb {N}$
by
$g: \mathbb {N}\to \mathbb {N}$
by
We claim that
![]() $I'\circ I$
and g witness that
$I'\circ I$
and g witness that
![]() $r'\circ r$
is
$r'\circ r$
is
![]() $\kappa $
-eventually definable. To verify this let
$\kappa $
-eventually definable. To verify this let
![]() $x\in \{0,1\}^*$
satisfy
$x\in \{0,1\}^*$
satisfy
![]() $|x|\geqslant g(k)$
where
$|x|\geqslant g(k)$
where
![]() $k:= \kappa (x)$
. Then
$k:= \kappa (x)$
. Then
![]() $|r(x)|\geqslant |x|^{1/c}\geqslant h'(f(k))\geqslant h'(\kappa '(r(x)))$
using that
$|r(x)|\geqslant |x|^{1/c}\geqslant h'(f(k))\geqslant h'(\kappa '(r(x)))$
using that
![]() $h'$
is nondecreasing. Hence
$h'$
is nondecreasing. Hence
![]() $\mathcal S(r(x))^{I'}\cong {\mathcal S}(r'(r(x)))$
. As
$\mathcal S(r(x))^{I'}\cong {\mathcal S}(r'(r(x)))$
. As
![]() $|x|\geqslant g(k)\geqslant h(k)$
, we conclude
$|x|\geqslant g(k)\geqslant h(k)$
, we conclude
![]() ${\mathcal S}(x)^I\cong {\mathcal S}(r(x))$
, which implies
${\mathcal S}(x)^I\cong {\mathcal S}(r(x))$
, which implies
![]() ${\mathcal S}(x)^{I'\circ I}\cong {\mathcal S}(r'(r(x)))$
.
${\mathcal S}(x)^{I'\circ I}\cong {\mathcal S}(r'(r(x)))$
.
Definition 3.5. Let
![]() $(Q, \kappa )$
and
$(Q, \kappa )$
and
![]() $(Q', \kappa ')$
be parameterized problems. An eventually definable reduction from
$(Q', \kappa ')$
be parameterized problems. An eventually definable reduction from
![]() $(Q, \kappa )$
to
$(Q, \kappa )$
to
![]() $(Q', \kappa ')$
is a parameterized reduction from
$(Q', \kappa ')$
is a parameterized reduction from
![]() $(Q, \kappa )$
to
$(Q, \kappa )$
to
![]() $(Q', \kappa ')$
that is honest and
$(Q', \kappa ')$
that is honest and
![]() $\kappa $
-eventually definable.
$\kappa $
-eventually definable.
Example 3.6. There is an eventually definable reduction from ![]() to
to ![]() .
.
Proof Let
![]() $P:\{0,1\}^*\to \{0,1\}^*$
map a nondeterministic Turing machine
$P:\{0,1\}^*\to \{0,1\}^*$
map a nondeterministic Turing machine
![]() $\mathbb M$
to another
$\mathbb M$
to another
![]() $\mathbb M'$
that simulates
$\mathbb M'$
that simulates
![]() $\mathbb M$
and, if
$\mathbb M$
and, if
![]() $\mathbb M$
accepts, then
$\mathbb M$
accepts, then
![]() $\mathbb M'$
nondeterministically makes any number of steps before it halts and accepts; strings x not encoding machines are mapped to themselves. This is clearly a parameterized reduction. By Example 3.3,
$\mathbb M'$
nondeterministically makes any number of steps before it halts and accepts; strings x not encoding machines are mapped to themselves. This is clearly a parameterized reduction. By Example 3.3,
![]() $\langle 1^n,x\rangle \mapsto \langle 1^n,P(x)\rangle $
is eventually definable.
$\langle 1^n,x\rangle \mapsto \langle 1^n,P(x)\rangle $
is eventually definable.
Recall that this function outputs
![]() $0$
on strings y not of the desired form
$0$
on strings y not of the desired form
![]() $ \langle 1^n,x \rangle $
, i.e., the interpretation produces a structure isomorphic to
$ \langle 1^n,x \rangle $
, i.e., the interpretation produces a structure isomorphic to
![]() ${\mathcal S}(0)$
. We change the interpretation to output
${\mathcal S}(0)$
. We change the interpretation to output
![]() ${\mathcal S}(y)$
in this case. This ensures honesty (we can assume
${\mathcal S}(y)$
in this case. This ensures honesty (we can assume
![]() $|\mathbb M'|\geqslant |\mathbb M|$
) and thus gives a reduction as desired.
$|\mathbb M'|\geqslant |\mathbb M|$
) and thus gives a reduction as desired.
Remark 3.7. A parameterized problem
![]() $(Q,\kappa )$
is in
$(Q,\kappa )$
is in
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
if and only if Q is decidable and there is an eventually definable reduction from
$\mathsf {para}\text {-}\mathsf {AC}^0$
if and only if Q is decidable and there is an eventually definable reduction from
![]() $(Q,\kappa )$
to a trivial problem, say,
$(Q,\kappa )$
to a trivial problem, say,
![]() $(Q_0, \kappa _0)$
for
$(Q_0, \kappa _0)$
for
![]() $Q_0$
the set of strings starting with
$Q_0$
the set of strings starting with
![]() $0$
and
$0$
and
![]() $\kappa _0$
is constantly
$\kappa _0$
is constantly
![]() $0$
.
$0$
.
It is straightforward to check that this reducibility is transitive and preserves membership in
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
:
$\mathsf {para}\text {-}\mathsf {AC}^0$
:
Lemma 3.8. Assume that there is an eventually definable reduction from
![]() $(Q, \kappa )$
to
$(Q, \kappa )$
to
![]() $(Q', \kappa ')$
.
$(Q', \kappa ')$
.
-
(i) If there is an eventually definable reduction from
 $(Q', \kappa ')$
to
$(Q', \kappa ')$
to
 $(Q", \kappa ")$
, then there is one from
$(Q", \kappa ")$
, then there is one from
 $(Q, \kappa )$
to
$(Q, \kappa )$
to
 $(Q", \kappa ")$
.
$(Q", \kappa ")$
. -
(ii) If
 $(Q', \kappa ')\in \mathsf {para}\text {-}\mathsf {AC}^0$
and Q is decidable, then
$(Q', \kappa ')\in \mathsf {para}\text {-}\mathsf {AC}^0$
and Q is decidable, then
 $(Q, \kappa )\in \mathsf {para}\text {-}\mathsf {AC}^0$
.
$(Q, \kappa )\in \mathsf {para}\text {-}\mathsf {AC}^0$
.
3.2 The complexity of 
It is known that the question whether ![]() is fixed-parameter tractable is closely related to the relationship of
is fixed-parameter tractable is closely related to the relationship of
![]() $\mathsf {E}$
and
$\mathsf {E}$
and
![]() $\mathsf {NE}$
:
$\mathsf {NE}$
:
Theorem 3.9 [Reference Aumann and Dombb4, Reference Chen and Flum7].
![]() if and only if
if and only if
![]() $\mathsf {NE}\subseteq \mathsf {E}$
.
$\mathsf {NE}\subseteq \mathsf {E}$
.
Theorem 1.2(i) is a
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
-analogue of this result.
$\mathsf {para}\text {-}\mathsf {AC}^0$
-analogue of this result.
Theorem 1.2.
-
(i)
 if and only if
if and only if
 $\mathsf {NE}\subseteq \mathsf {LINH}$
.
$\mathsf {NE}\subseteq \mathsf {LINH}$
. -
(ii)
 implies
implies  .
.
Proof (ii) follows from Example 3.6 and Lemma 3.8. Alternatively, let
![]() $(\mathsf C_{n,k})_{n,k}$
witness
$(\mathsf C_{n,k})_{n,k}$
witness ![]() according to Proposition 2.2(b). Then
according to Proposition 2.2(b). Then
![]() $(\bigvee _{m\leqslant n}\mathsf C^n_{m,k})_{n,k}$
witnesses
$(\bigvee _{m\leqslant n}\mathsf C^n_{m,k})_{n,k}$
witnesses ![]() where
where
![]() $\mathsf C^n_{m,k}$
checks its input has the form
$\mathsf C^n_{m,k}$
checks its input has the form
![]() $\langle 1^n,x\rangle $
for some
$\langle 1^n,x\rangle $
for some
![]() $x\in \{0,1\}^k$
and then runs
$x\in \{0,1\}^k$
and then runs
![]() $\mathsf C_{m,k}$
on
$\mathsf C_{m,k}$
on
![]() $\langle 1^m,x\rangle $
.
$\langle 1^m,x\rangle $
.
To prove (i), first assume
![]() $\mathsf {NE}\subseteq \mathsf {LINH}$
and let Q be the classical problem underlying
$\mathsf {NE}\subseteq \mathsf {LINH}$
and let Q be the classical problem underlying ![]() but with input n encoded in binary:
but with input n encoded in binary:

Clearly,
![]() $Q\in \mathsf {NE}$
, so by assumption and Proposition 2.1(iii) we have
$Q\in \mathsf {NE}$
, so by assumption and Proposition 2.1(iii) we have
![]() $\mathit {un}(Q)\in \mathsf {AC}^0$
. Recall
$\mathit {un}(Q)\in \mathsf {AC}^0$
. Recall
 $$ \begin{align*} \mathit{un}(Q)= \bigg\{1^{\mathit{num}(\langle \mathit{bin}(n), \mathbb M\rangle)} \;\Big|\; \begin{array}{l} \text{the nondeterministic Turing machine } {\mathbb M} \\ \text{accepts the empty input in exactly } n \text{ steps} \end{array}\!\!\! \bigg\}. \end{align*} $$
$$ \begin{align*} \mathit{un}(Q)= \bigg\{1^{\mathit{num}(\langle \mathit{bin}(n), \mathbb M\rangle)} \;\Big|\; \begin{array}{l} \text{the nondeterministic Turing machine } {\mathbb M} \\ \text{accepts the empty input in exactly } n \text{ steps} \end{array}\!\!\! \bigg\}. \end{align*} $$
By Example 3.2 the map
![]() $ \langle 1^n, \mathbb M \rangle \mapsto 1^{\mathit {num}( \langle \mathit {bin}(n), \mathbb M \rangle )}$
is eventually definable with respect to the parameterization of
$ \langle 1^n, \mathbb M \rangle \mapsto 1^{\mathit {num}( \langle \mathit {bin}(n), \mathbb M \rangle )}$
is eventually definable with respect to the parameterization of ![]() . It is an honest parameterized reduction to
. It is an honest parameterized reduction to
![]() $(\mathit {un}(Q), \kappa )$
where
$(\mathit {un}(Q), \kappa )$
where
![]() $\kappa $
maps
$\kappa $
maps
![]() $1^{\mathit {num}( \langle \mathit {bin}(n), \mathbb M \rangle )}$
to
$1^{\mathit {num}( \langle \mathit {bin}(n), \mathbb M \rangle )}$
to
![]() $|\mathbb {M}|$
. Since
$|\mathbb {M}|$
. Since
![]() $(\mathit {un}(Q), \kappa )\in \mathsf {para}\text {-}\mathsf {AC}^0$
, Lemma 3.8 implies
$(\mathit {un}(Q), \kappa )\in \mathsf {para}\text {-}\mathsf {AC}^0$
, Lemma 3.8 implies ![]() .
.
Conversely, assume ![]() . Let
. Let
![]() $Q\subseteq \{0,1\}^*$
be a problem in
$Q\subseteq \{0,1\}^*$
be a problem in
![]() $\mathsf {NE}$
. To show that
$\mathsf {NE}$
. To show that
![]() $Q\in \mathsf {LINH}$
, it suffices to prove
$Q\in \mathsf {LINH}$
, it suffices to prove
![]() $\mathit {un}(Q)\in \mathsf {AC}^0$
again by Proposition 2.1(iii).
$\mathit {un}(Q)\in \mathsf {AC}^0$
again by Proposition 2.1(iii).
As
![]() $Q \in \mathsf {NE}$
there is a constant
$Q \in \mathsf {NE}$
there is a constant
![]() $c\in \mathbb {N}$
and a nondeterministic Turing machine
$c\in \mathbb {N}$
and a nondeterministic Turing machine
![]() $\mathbb M$
accepting Q that on input x halts in time at most
$\mathbb M$
accepting Q that on input x halts in time at most
![]() $\mathit {num}(x)^c-2|x|-2$
. Consider the nondeterministic Turing machine
$\mathit {num}(x)^c-2|x|-2$
. Consider the nondeterministic Turing machine
![]() ${\mathbb M}^*$
that started with the empty input runs as follows:
${\mathbb M}^*$
that started with the empty input runs as follows:

Line 1 takes exactly
![]() $2|y|+2$
many steps by moving the head forth and back on some tape, so the dummy steps in line 4 are possible. Since
$2|y|+2$
many steps by moving the head forth and back on some tape, so the dummy steps in line 4 are possible. Since
![]() $\mathit {num}$
is injective, we have
$\mathit {num}$
is injective, we have
Since
![]() $\mathbb M^*$
is a fixed machine,
$\mathbb M^*$
is a fixed machine, ![]() implies that the classical problem
implies that the classical problem
is in
![]() $\mathsf {AC}^0$
. Choose a first-order sentence
$\mathsf {AC}^0$
. Choose a first-order sentence
![]() $\varphi $
for
$\varphi $
for
![]() $Q'$
according to Theorem 2.6. Lemma 2.9 gives an interpretation
$Q'$
according to Theorem 2.6. Lemma 2.9 gives an interpretation
![]() ${\mathit I} $
such that
${\mathit I} $
such that
![]() ${\mathcal S}(1^n)^{{\mathit I}}\cong \mathcal S(1^{n^c})$
for all
${\mathcal S}(1^n)^{{\mathit I}}\cong \mathcal S(1^{n^c})$
for all
![]() $n>1$
. Then
$n>1$
. Then
![]() $1^{n^c}\in Q'$
is equivalent to
$1^{n^c}\in Q'$
is equivalent to
![]() $\mathcal S(1^n)\models \varphi ^{{\mathit I}} $
. Thus the r.h.s. in (2) is equivalent to
$\mathcal S(1^n)\models \varphi ^{{\mathit I}} $
. Thus the r.h.s. in (2) is equivalent to
![]() ${\mathcal S}(1^{\mathit {num}(x)})\models \varphi ^{{\mathit I}}$
provided
${\mathcal S}(1^{\mathit {num}(x)})\models \varphi ^{{\mathit I}}$
provided
![]() $\mathit {num}(x)>1$
, i.e., x is non-empty. The l.h.s. in (2) is equivalent to
$\mathit {num}(x)>1$
, i.e., x is non-empty. The l.h.s. in (2) is equivalent to
![]() $1^{\mathit {num}(x)}\in \mathit {un}(Q)$
. Thus
$1^{\mathit {num}(x)}\in \mathit {un}(Q)$
. Thus
![]() $\varphi ^{{\mathit I}}$
witnesses that
$\varphi ^{{\mathit I}}$
witnesses that
![]() $\mathit {un}(Q)\in \mathsf {AC}^0$
according to Theorem 2.6.
$\mathit {un}(Q)\in \mathsf {AC}^0$
according to Theorem 2.6.
3.3 Almost tally problems
Recall that a classical problem
![]() $Q\subseteq \{0,1\}^*$
is tally if
$Q\subseteq \{0,1\}^*$
is tally if
![]() $Q\subseteq \{1\}^*$
. All parameterized problems mentioned in the introduction are almost tally in the following sense:
$Q\subseteq \{1\}^*$
. All parameterized problems mentioned in the introduction are almost tally in the following sense:
Definition 3.11. A parameterized problem
![]() $(Q,\kappa )$
is almost tally if
$(Q,\kappa )$
is almost tally if
and there is a computable
![]() $f:\mathbb {N}\to \mathbb {N}$
such that for all
$f:\mathbb {N}\to \mathbb {N}$
such that for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $x\in \{0,1\}^*$
$x\in \{0,1\}^*$
Theorem 1.2(ii) holds not only for ![]() but for every almost tally problem in
but for every almost tally problem in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
. In fact,
$\mathsf {para}\text {-}\mathsf {NP}$
. In fact, ![]() is the hardest almost tally problem in
is the hardest almost tally problem in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
:
$\mathsf {para}\text {-}\mathsf {NP}$
:
Lemma 3.12. For every almost tally problem in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
there is an eventually definable reduction to
$\mathsf {para}\text {-}\mathsf {NP}$
there is an eventually definable reduction to ![]() .
.
Proof Let
![]() $(Q, \kappa )\in \mathsf {para}\text {-}\mathsf {NP}$
be almost tally. The identity is a parameterized reduction from
$(Q, \kappa )\in \mathsf {para}\text {-}\mathsf {NP}$
be almost tally. The identity is a parameterized reduction from
![]() $(Q, \kappa )$
to its re-parameterization
$(Q, \kappa )$
to its re-parameterization
![]() $(Q, \kappa ')$
where
$(Q, \kappa ')$
where
![]() $\kappa '( \langle 1^n, x \rangle ):=|x|$
for all
$\kappa '( \langle 1^n, x \rangle ):=|x|$
for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $x\in \{0,1\}^*$
. Hence, the identity is an eventually definable reduction. We can therefore assume that
$x\in \{0,1\}^*$
. Hence, the identity is an eventually definable reduction. We can therefore assume that
![]() $\kappa = \kappa '$
.
$\kappa = \kappa '$
.
Let
![]() $\mathbb M$
be a nondeterministic Turing machine that accepts Q and on input
$\mathbb M$
be a nondeterministic Turing machine that accepts Q and on input
![]() $ \langle 1^n, x \rangle $
runs in time at most
$ \langle 1^n, x \rangle $
runs in time at most
![]() $f(k)\cdot n^{c}$
where
$f(k)\cdot n^{c}$
where
![]() $c\in \mathbb {N}$
,
$c\in \mathbb {N}$
,
![]() $f: \mathbb {N}\to \mathbb {N}$
is a computable function, and
$f: \mathbb {N}\to \mathbb {N}$
is a computable function, and
![]() $k:=|x|$
.
$k:=|x|$
.
Define
![]() $g:\mathbb {N}^2\to \mathbb {N}$
by
$g:\mathbb {N}^2\to \mathbb {N}$
by
For
![]() $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
![]() $k:=|x|$
, consider the nondeterministic Turing machine
$k:=|x|$
, consider the nondeterministic Turing machine
![]() $\mathbb M_x$
that on the empty input runs as follows:
$\mathbb M_x$
that on the empty input runs as follows:

Step 1 can be implemented to take exactly
![]() $2+2m+2+2k$
many steps (recall (1)), so the dummy steps in line 4 are possible if
$2+2m+2+2k$
many steps (recall (1)), so the dummy steps in line 4 are possible if
![]() $m>f(k)$
. Note that for each k, the function
$m>f(k)$
. Note that for each k, the function
![]() $m\mapsto g(m,k)$
is injective. Thus, if
$m\mapsto g(m,k)$
is injective. Thus, if
![]() $n>f(k)$
, we have
$n>f(k)$
, we have
Using Example 3.3, one easily constructs an eventually definable reduction that maps
![]() $ \langle 1^n,x \rangle $
to
$ \langle 1^n,x \rangle $
to
![]() $ \langle 1^{g(n,k)+1}, \mathbb M_x \rangle $
.
$ \langle 1^{g(n,k)+1}, \mathbb M_x \rangle $
.
It is straightforward to infer from Proposition 2.1 that
![]() $\mathsf {NE}\subseteq \mathsf {LINH}$
if and only if every tally problem in
$\mathsf {NE}\subseteq \mathsf {LINH}$
if and only if every tally problem in
![]() $\mathsf {NP}$
is in
$\mathsf {NP}$
is in
![]() $\mathsf {AC}^0$
. We don’t know of a similarly easy proof of the following parameterized variant of this observation. Instead, our proof relies on our analysis of
$\mathsf {AC}^0$
. We don’t know of a similarly easy proof of the following parameterized variant of this observation. Instead, our proof relies on our analysis of ![]() :
:
Corollary 3.13.
![]() $\mathsf {NE}\subseteq \mathsf {LINH}$
if and only if every almost tally problem in
$\mathsf {NE}\subseteq \mathsf {LINH}$
if and only if every almost tally problem in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
is in
$\mathsf {para}\text {-}\mathsf {NP}$
is in
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
.
$\mathsf {para}\text {-}\mathsf {AC}^0$
.
3.4 Variants
For the optimistic reader, Corollary 3.13 gives an approach to separate
![]() $\mathsf {NE}$
from
$\mathsf {NE}$
from
![]() $\mathsf {LINH}$
. From this perspective, it is of interest to ask whether finding an almost tally problem outside
$\mathsf {LINH}$
. From this perspective, it is of interest to ask whether finding an almost tally problem outside
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
but in a natural subclass of
$\mathsf {para}\text {-}\mathsf {AC}^0$
but in a natural subclass of
![]() $\mathsf {para}\text {-}\mathsf {NP}$
implies stronger separations of natural complexity classes. We verify the following variants of Corollary 3.13:
$\mathsf {para}\text {-}\mathsf {NP}$
implies stronger separations of natural complexity classes. We verify the following variants of Corollary 3.13:
Lemma 3.14.
-
(i)
 $\mathsf {E}\subseteq \mathsf {LINH}$
if and only if every almost tally problem in
$\mathsf {E}\subseteq \mathsf {LINH}$
if and only if every almost tally problem in
 $\mathsf {FPT}$
is in
$\mathsf {FPT}$
is in
 $\mathsf {para}\text {-}\mathsf {AC}^0$
.
$\mathsf {para}\text {-}\mathsf {AC}^0$
. -
(ii)
 $\mathsf {NLINSPACE}\subseteq \mathsf {LINH}$
if and only if every almost tally problem in
$\mathsf {NLINSPACE}\subseteq \mathsf {LINH}$
if and only if every almost tally problem in
 $\mathsf {para}\text {-}\mathsf {NL}$
is in
$\mathsf {para}\text {-}\mathsf {NL}$
is in
 $\mathsf {para}\text {-}\mathsf {AC}^0$
.
$\mathsf {para}\text {-}\mathsf {AC}^0$
. -
(iii)
 $\mathsf {LINSPACE}\subseteq \mathsf {LINH}$
if and only if every almost tally problem in
$\mathsf {LINSPACE}\subseteq \mathsf {LINH}$
if and only if every almost tally problem in
 $\mathsf {para}\text {-}\mathsf {L}$
is in
$\mathsf {para}\text {-}\mathsf {L}$
is in
 $\mathsf {para}\text {-}\mathsf {AC}^0$
.
$\mathsf {para}\text {-}\mathsf {AC}^0$
.
Proof The proof of (i) is analogous to the proof of Corollary 3.13 using the subproblem of ![]() where the input machine
where the input machine
![]() $\mathbb M$
is deterministic. Similarly the proof of (iii) is analogous to the proof of (ii). We show how (ii) is proved by modifying the proof of Corollary 3.13.
$\mathbb M$
is deterministic. Similarly the proof of (iii) is analogous to the proof of (ii). We show how (ii) is proved by modifying the proof of Corollary 3.13.
Consider the following variant of ![]() :
:

Here, the space
![]() $\left \lfloor \log m\right \rfloor $
of a run bounds all work tapes together, that is, if
$\left \lfloor \log m\right \rfloor $
of a run bounds all work tapes together, that is, if
![]() $c_i$
is the maximal cell number visited on work tape i, then
$c_i$
is the maximal cell number visited on work tape i, then
![]() $\sum _ic_i\leqslant \left \lfloor \log m\right \rfloor $
.
$\sum _ic_i\leqslant \left \lfloor \log m\right \rfloor $
.
It is clear that this problem is in
![]() $\mathsf {para}\text {-}\mathsf {NL}$
.
$\mathsf {para}\text {-}\mathsf {NL}$
.
Claim 1.
![]() if and only if
if and only if
![]() $\mathsf {NLINSPACE}\subseteq \mathsf {LINH}$
.
$\mathsf {NLINSPACE}\subseteq \mathsf {LINH}$
.
Proof of Claim 1
Assume
![]() $\mathsf {NLINSPACE}\subseteq \mathsf {LINH}$
and let Q be the classical problem underlying
$\mathsf {NLINSPACE}\subseteq \mathsf {LINH}$
and let Q be the classical problem underlying ![]() but with the inputs
but with the inputs
![]() $n, m$
encoded in binary. Clearly,
$n, m$
encoded in binary. Clearly,
![]() $Q\in \mathsf {NLINSPACE} \subseteq \mathsf {LINH}$
, so
$Q\in \mathsf {NLINSPACE} \subseteq \mathsf {LINH}$
, so
![]() $\mathit {un}(Q)\in \mathsf {AC}^0$
by Proposition 2.1(iii). Similarly as Example 3.2 one sees that
$\mathit {un}(Q)\in \mathsf {AC}^0$
by Proposition 2.1(iii). Similarly as Example 3.2 one sees that
is eventually definable. Then ![]() follows as in Theorem 1.2(i).
follows as in Theorem 1.2(i).
Conversely, assume ![]() and let
and let
![]() $Q\in \mathsf {NLINSPACE}$
. Choose a nondeterministic Turing machine
$Q\in \mathsf {NLINSPACE}$
. Choose a nondeterministic Turing machine
![]() $\mathbb M$
accepting Q that on input
$\mathbb M$
accepting Q that on input
![]() $x\in \{0,1\}^*$
runs in time at most
$x\in \{0,1\}^*$
runs in time at most
 $$\begin{align*}\frac{\mathit{num}(x)^{c}}{10c(|x|+2)} - 10c(|x|+ 2)- |x| \end{align*}$$
$$\begin{align*}\frac{\mathit{num}(x)^{c}}{10c(|x|+2)} - 10c(|x|+ 2)- |x| \end{align*}$$
and uses space at most
![]() $c\cdot |x|$
; here
$c\cdot |x|$
; here
![]() $c\in \mathbb {N}$
is a suitable constant. Define
$c\in \mathbb {N}$
is a suitable constant. Define
![]() $\mathbb M^*$
as in the proof of Theorem 1.2 but with the following implementation details. For the simulation in line 2, first initialize a length
$\mathbb M^*$
as in the proof of Theorem 1.2 but with the following implementation details. For the simulation in line 2, first initialize a length
![]() $c(|y|+ 2)$
binary counter using exactly
$c(|y|+ 2)$
binary counter using exactly
![]() $10c(|y|+ 2)$
steps, and increase it using exactly
$10c(|y|+ 2)$
steps, and increase it using exactly
![]() $10c(|y|+ 2)$
many steps for each simulated step of
$10c(|y|+ 2)$
many steps for each simulated step of
![]() $\mathbb M$
. In line 4 continue increasing the counter in this way until it reaches
$\mathbb M$
. In line 4 continue increasing the counter in this way until it reaches
![]() $\mathit {num}(y)^c/(10c(|y|+ 2))$
. For long enough y, the binary representation of this number can be computed in time at most
$\mathit {num}(y)^c/(10c(|y|+ 2))$
. For long enough y, the binary representation of this number can be computed in time at most
![]() $\mathit {num}(y)$
and space
$\mathit {num}(y)$
and space
![]() $O(|y|)$
(where the constant in the O-notation depends on c). This computation can be done in parallel to the simulation in lines 2 and 4. Hence, line 5 completes exactly
$O(|y|)$
(where the constant in the O-notation depends on c). This computation can be done in parallel to the simulation in lines 2 and 4. Hence, line 5 completes exactly
![]() $\mathit {num}(y)^c+1$
steps, and uses space at most
$\mathit {num}(y)^c+1$
steps, and uses space at most
![]() $d\cdot |y|$
for a suitable
$d\cdot |y|$
for a suitable
![]() $d\geqslant c$
.
$d\geqslant c$
.
Thus, we arrive at the following variant of (2). For long enough
![]() $x\in \{0,1\}^*$
:
$x\in \{0,1\}^*$
:
 $$ \begin{align*} x \in Q & \iff {\mathbb M}^* \text{ accepts the empty input in exactly } \mathit{num}(x)^c+1 \text{ many steps} \\ &\text{and space at most } \left\lfloor\log(\mathit{num}(x)^d)\right\rfloor. \end{align*} $$
$$ \begin{align*} x \in Q & \iff {\mathbb M}^* \text{ accepts the empty input in exactly } \mathit{num}(x)^c+1 \text{ many steps} \\ &\text{and space at most } \left\lfloor\log(\mathit{num}(x)^d)\right\rfloor. \end{align*} $$
Our assumption ![]() implies that the classical problem
implies that the classical problem
 $$ \begin{align*} Q':= \big\{\langle 1^n,1^m\rangle \;\big|\;\ & n\leqslant m \text{ and } \mathbb M^* \text{ accepts the empty input in exactly } n+1 \text{ many} \\ & \text{steps and space at most } \left\lfloor\log m\right\rfloor\big\} \end{align*} $$
$$ \begin{align*} Q':= \big\{\langle 1^n,1^m\rangle \;\big|\;\ & n\leqslant m \text{ and } \mathbb M^* \text{ accepts the empty input in exactly } n+1 \text{ many} \\ & \text{steps and space at most } \left\lfloor\log m\right\rfloor\big\} \end{align*} $$
is in
![]() $\mathsf {AC}^0$
. Now
$\mathsf {AC}^0$
. Now
![]() $\mathit {un}(Q)\in \mathsf {AC}^0$
(and hence
$\mathit {un}(Q)\in \mathsf {AC}^0$
(and hence
![]() $Q\in \mathsf {LINH}$
) follows as in Theorem 1.2(i) using an interpretation
$Q\in \mathsf {LINH}$
) follows as in Theorem 1.2(i) using an interpretation
![]() ${\mathit I} $
such that
${\mathit I} $
such that
![]() ${\mathcal S}(1^n)^{{\mathit I}}\cong {\mathcal S}(\big \langle 1^{n^c}, 1^{n^d}\big \rangle )$
.
${\mathcal S}(1^n)^{{\mathit I}}\cong {\mathcal S}(\big \langle 1^{n^c}, 1^{n^d}\big \rangle )$
.
Claim 2. For every almost tally problem in
![]() $\mathsf {para}\text {-}\mathsf {NL}$
there is an eventually definable reduction to
$\mathsf {para}\text {-}\mathsf {NL}$
there is an eventually definable reduction to ![]() .
.
Proof of Claim 2
Let
![]() $(Q, \kappa )\in \mathsf {para}\text {-}\mathsf {NL}$
be almost tally and
$(Q, \kappa )\in \mathsf {para}\text {-}\mathsf {NL}$
be almost tally and
![]() $\mathbb M$
be a nondeterministic Turing machine that accepts Q and that on input
$\mathbb M$
be a nondeterministic Turing machine that accepts Q and that on input
![]() $ \langle 1^n, x \rangle $
runs in time at most
$ \langle 1^n, x \rangle $
runs in time at most
![]() $f(k)\cdot n^{c}$
and space at most
$f(k)\cdot n^{c}$
and space at most
![]() $f(k)+ c\cdot \log n$
where
$f(k)+ c\cdot \log n$
where
![]() $c\in \mathbb {N}$
,
$c\in \mathbb {N}$
,
![]() $f:\mathbb {N}\to \mathbb {N}$
is a computable function, and
$f:\mathbb {N}\to \mathbb {N}$
is a computable function, and
![]() $k:= \kappa ( \langle 1^n, x \rangle )$
. We can assume
$k:= \kappa ( \langle 1^n, x \rangle )$
. We can assume
![]() $k= |x|$
(see the proof of Lemma 3.12).
$k= |x|$
(see the proof of Lemma 3.12).
For
![]() $x\in \{0, 1\}^*$
with
$x\in \{0, 1\}^*$
with
![]() $k:= |x|$
, define the nondeterministic Turing machine
$k:= |x|$
, define the nondeterministic Turing machine
![]() $\mathbb M_x$
as in the proof of Lemma 3.12 but with a different g (chosen below) and line 1 changed to nondeterministically write some
$\mathbb M_x$
as in the proof of Lemma 3.12 but with a different g (chosen below) and line 1 changed to nondeterministically write some
![]() $m\in \mathbb {N}$
in binary in exactly
$m\in \mathbb {N}$
in binary in exactly
![]() $2\left \lceil \log (m+ 1)\right \rceil + 2$
steps. The simulation in line 2 is done as in the previous claim maintaining a length
$2\left \lceil \log (m+ 1)\right \rceil + 2$
steps. The simulation in line 2 is done as in the previous claim maintaining a length
![]() $(c+1)\left \lceil \log (m+1)\right \rceil $
binary counter. It further maintains the position of
$(c+1)\left \lceil \log (m+1)\right \rceil $
binary counter. It further maintains the position of
![]() $\mathbb M$
’s head on the input tape which we can assume to be at most
$\mathbb M$
’s head on the input tape which we can assume to be at most
![]() $| \langle 1^m,x \rangle |+1$
and uses it to compute the currently scanned bit. Counter and position are updated for each simulated step of
$| \langle 1^m,x \rangle |+1$
and uses it to compute the currently scanned bit. Counter and position are updated for each simulated step of
![]() $\mathbb M$
. If
$\mathbb M$
. If
![]() $k< m$
, then one step of
$k< m$
, then one step of
![]() $\mathbb M$
is simulated in exactly
$\mathbb M$
is simulated in exactly
![]() $10c\left \lceil \log (m+1)\right \rceil $
steps. In line 4 the binary counter is updated until it reaches
$10c\left \lceil \log (m+1)\right \rceil $
steps. In line 4 the binary counter is updated until it reaches
![]() $m^{c+1}$
. Hence line 4 is completed after exactly
$m^{c+1}$
. Hence line 4 is completed after exactly
![]() $g(m,k):=m^{c+1}\cdot 10c\left \lceil \log (m+ 1)\right \rceil + 2\left \lceil \log (m+1)\right \rceil + 2$
steps. The dummy steps in line 4 are possible if
$g(m,k):=m^{c+1}\cdot 10c\left \lceil \log (m+ 1)\right \rceil + 2\left \lceil \log (m+1)\right \rceil + 2$
steps. The dummy steps in line 4 are possible if
![]() $m>f(k)$
. In this case the computation takes space at most
$m>f(k)$
. In this case the computation takes space at most
![]() $d\log m$
for suitable
$d\log m$
for suitable
![]() $d\in \mathbb {N}$
. Thus, if
$d\in \mathbb {N}$
. Thus, if
![]() $n> f(k)$
, we have
$n> f(k)$
, we have
Similarly as seen in the proof of Lemma 3.12, this implies the claim.
It now suffices to show that ![]() if and only if every almost tally problem in
if and only if every almost tally problem in
![]() $\mathsf {para}\text {-}\mathsf {NL}$
is in
$\mathsf {para}\text {-}\mathsf {NL}$
is in
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
. The forward direction follows from Claim 2 and Lemma 3.8. And if
$\mathsf {para}\text {-}\mathsf {AC}^0$
. The forward direction follows from Claim 2 and Lemma 3.8. And if ![]() , then we get an almost tally problem in
, then we get an almost tally problem in
![]() $\mathsf {para}\text {-}\mathsf {NL} \setminus \mathsf {para}\text {-}\mathsf {AC}^0$
by rewriting inputs
$\mathsf {para}\text {-}\mathsf {NL} \setminus \mathsf {para}\text {-}\mathsf {AC}^0$
by rewriting inputs
![]() $ \langle 1^n, 1^m, \mathbb M \rangle $
of
$ \langle 1^n, 1^m, \mathbb M \rangle $
of ![]() to
to
![]() $ \langle 1^{ \langle n, m \rangle }, \mathbb M \rangle $
where
$ \langle 1^{ \langle n, m \rangle }, \mathbb M \rangle $
where
![]() $ \langle n, m \rangle $
is a pairing function on
$ \langle n, m \rangle $
is a pairing function on
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
We find it worthwhile to explicitly point out the following direct corollary concerning the parameterized halting problem for deterministic Turing machines:
Corollary 3.15. If ![]() , then
, then
![]() $\mathsf {E}\not \subseteq \mathsf {LINH}$
.
$\mathsf {E}\not \subseteq \mathsf {LINH}$
.

4 On the parameterized complexity of 
Recall, the problem ![]() asks whether a given
asks whether a given
![]() $n\in \mathbb {N}$
in unary satisfies a given
$n\in \mathbb {N}$
in unary satisfies a given
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (x)$
, parameterized by the length of
$\varphi (x)$
, parameterized by the length of
![]() $\varphi $
. Further recall that
$\varphi $
. Further recall that
![]() $\Delta _0$
refers to the language
$\Delta _0$
refers to the language
![]() $L_{\text {ar}}$
with function symbols
$L_{\text {ar}}$
with function symbols
![]() $+,\cdot $
and contains the
$+,\cdot $
and contains the
![]() $L_{\text {ar}}$
-formulas with quantifiers bounded by
$L_{\text {ar}}$
-formulas with quantifiers bounded by
![]() $L_{\text {ar}} $
-terms.
$L_{\text {ar}} $
-terms.
This section first observes that ![]() is “the same” as a basic parameterized model-checking problem, uses this to prove the lower bound
is “the same” as a basic parameterized model-checking problem, uses this to prove the lower bound ![]() (Theorem 1.4), and finally, based on the previous section, infers consequences from upper bounds on the parameterized complexity of
(Theorem 1.4), and finally, based on the previous section, infers consequences from upper bounds on the parameterized complexity of ![]() , including Theorem 1.3.
, including Theorem 1.3.
4.1 Model-checking arithmetic
Recall
![]() $L^{\text {r}}_{\text {ar}}$
is the relational version of the language of arithmetic
$L^{\text {r}}_{\text {ar}}$
is the relational version of the language of arithmetic
![]() $L_{\text {ar}}$
. We observe that
$L_{\text {ar}}$
. We observe that ![]() is “the same” as the parameterized model-checking problem for first-order logic over finite standard
is “the same” as the parameterized model-checking problem for first-order logic over finite standard
![]() $L^{\text {r}}_{\text {ar}}$
-structures:
$L^{\text {r}}_{\text {ar}}$
-structures:

Lemma 4.1. There is a computable function that maps every
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (x)$
to an
$\varphi (x)$
to an
![]() $L^{\text {r}}_{\text {ar}}$
-sentence
$L^{\text {r}}_{\text {ar}}$
-sentence
![]() $\psi $
such that for all
$\psi $
such that for all
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n>1$
:
$n>1$
:
Further, there is a computable function that maps every
![]() $L^{\text {r}}_{\text {ar}}$
-sentence
$L^{\text {r}}_{\text {ar}}$
-sentence
![]() $\psi $
to a
$\psi $
to a
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (x)$
such that (3) holds all
$\varphi (x)$
such that (3) holds all
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n>1$
.
$n>1$
.
Proof For the second assertion define
![]() $\varphi (x)$
as
$\varphi (x)$
as
![]() $\psi ^{<x}$
with atoms rewritten in the functional language
$\psi ^{<x}$
with atoms rewritten in the functional language
![]() $L_{\text {ar}}$
. The first assertion is folklore, see [Reference Gaifman and Dimitracopoulos22, Proposition 2.2]. We give a brief sketch for completeness. It is routine to compute, given a
$L_{\text {ar}}$
. The first assertion is folklore, see [Reference Gaifman and Dimitracopoulos22, Proposition 2.2]. We give a brief sketch for completeness. It is routine to compute, given a
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (\bar x)$
, a constant
$\varphi (\bar x)$
, a constant
![]() $c_\varphi>1$
and an
$c_\varphi>1$
and an
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\psi _0(\bar x)$
such that
$\psi _0(\bar x)$
such that
for all
![]() $\bar n,m\in \mathbb {N}$
with
$\bar n,m\in \mathbb {N}$
with
![]() $m\geqslant \text {max}\{\bar n,2\}^{c_\varphi }$
. Hence, for
$m\geqslant \text {max}\{\bar n,2\}^{c_\varphi }$
. Hence, for
![]() $n>1$
, the truth of
$n>1$
, the truth of
![]() $\varphi (n)$
is equivalent to
$\varphi (n)$
is equivalent to
![]() $n^{c_\varphi } \models \psi _0(n)$
. Since the number n is definable in the standard
$n^{c_\varphi } \models \psi _0(n)$
. Since the number n is definable in the standard
![]() $L^{\text {r}}_{\text {ar}}$
-structure
$L^{\text {r}}_{\text {ar}}$
-structure
![]() $n^{c_\varphi }$
(as the minimal element whose
$n^{c_\varphi }$
(as the minimal element whose
![]() $c_\varphi $
th power does not exist), we can replace
$c_\varphi $
th power does not exist), we can replace
![]() $\psi _0(n)$
by some sentence
$\psi _0(n)$
by some sentence
![]() $\psi _1$
. Then set
$\psi _1$
. Then set
![]() $\psi :=\psi _1^{{\mathit I} _{c_\varphi }}$
for the interpretation
$\psi :=\psi _1^{{\mathit I} _{c_\varphi }}$
for the interpretation
![]() ${\mathit I} _{c_\varphi }$
from Lemma 2.9.
${\mathit I} _{c_\varphi }$
from Lemma 2.9.
4.2 A lower bound
In this subsection we prove the following.
Theorem 1.4.
![]() .
.
We fix a proper elementary extension M of the standard
![]() $L_{\text {ar}}^{\text {r}}$
-model
$L_{\text {ar}}^{\text {r}}$
-model
![]() $\mathbb {N}$
, and a nonstandard element
$\mathbb {N}$
, and a nonstandard element
![]() $a\in M\setminus \mathbb {N}$
. We let
$a\in M\setminus \mathbb {N}$
. We let
![]() $<^M$
denote the interpretation of
$<^M$
denote the interpretation of
![]() $<$
in M. We need a simple lemma:
$<$
in M. We need a simple lemma:
Lemma 4.2. Let
![]() $f: \mathbb {N}\to \mathbb {N}$
be a computable function. Then there is an
$f: \mathbb {N}\to \mathbb {N}$
be a computable function. Then there is an
![]() $L_{\text {ar}}^{\text {r}}$
-formula
$L_{\text {ar}}^{\text {r}}$
-formula
![]() $\chi _f(x, y)$
such that for every
$\chi _f(x, y)$
such that for every
![]() $k\in \mathbb {N}$
and every
$k\in \mathbb {N}$
and every
![]() $b\in M$
:
$b\in M$
:
Proof Choose
![]() $\varphi _f(x,y,\bar z)$
according to Remark 2.5, and set
$\varphi _f(x,y,\bar z)$
according to Remark 2.5, and set
![]() $\chi _f(x,y):=\exists \bar z\varphi _f(x,y,\bar z)$
. In particular,
$\chi _f(x,y):=\exists \bar z\varphi _f(x,y,\bar z)$
. In particular,
![]() $\varphi _f$
is quantifier-free, so
$\varphi _f$
is quantifier-free, so
![]() $\chi _f^{<a}=\exists \bar z{<}a\ \varphi _f$
. Let
$\chi _f^{<a}=\exists \bar z{<}a\ \varphi _f$
. Let
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $ b\in M$
.
$ b\in M$
.
If
![]() $b=f(k)$
, then
$b=f(k)$
, then
![]() $\mathbb {N}\models \varphi _f(k,b,\bar m)$
for some
$\mathbb {N}\models \varphi _f(k,b,\bar m)$
for some
![]() $\bar m\in \mathbb {N}^{|\bar z|}$
since
$\bar m\in \mathbb {N}^{|\bar z|}$
since
![]() $\chi _f(x,y)$
defines f. Then
$\chi _f(x,y)$
defines f. Then
![]() $\bar m<^M a$
and
$\bar m<^M a$
and
![]() $M\models \varphi _f(k,b,\bar m)$
, so
$M\models \varphi _f(k,b,\bar m)$
, so
![]() $M\models \chi _f^{<a}(k,b)$
.
$M\models \chi _f^{<a}(k,b)$
.
If
![]() $M \models \chi _f^{<a}(k,b)$
, then both
$M \models \chi _f^{<a}(k,b)$
, then both
![]() $M\models \chi _f(k,b)$
and
$M\models \chi _f(k,b)$
and
![]() $M\models \chi _f(k,f(k))$
. But
$M\models \chi _f(k,f(k))$
. But
![]() $\chi _f(x,y)$
defines a function in
$\chi _f(x,y)$
defines a function in
![]() $\mathbb {N}$
and hence in M (by elementarity of the extension), so
$\mathbb {N}$
and hence in M (by elementarity of the extension), so
![]() $b=f(k)$
.
$b=f(k)$
.
Some notation: for
![]() $n\in \mathbb {N}$
define the
$n\in \mathbb {N}$
define the
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\text {"}x{=}n\text {"}$
by
$\text {"}x{=}n\text {"}$
by
![]() $\text {"}x{=}0\text {"}:= x{=}0$
and
$\text {"}x{=}0\text {"}:= x{=}0$
and
![]() $\text {"}x{=}(n+1)\text {"}:=\exists y(\text {"}y{=}n\text {"}\wedge +(y,1,x))$
. For an
$\text {"}x{=}(n+1)\text {"}:=\exists y(\text {"}y{=}n\text {"}\wedge +(y,1,x))$
. For an
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\varphi (y, \bar x)$
set
$\varphi (y, \bar x)$
set
![]() $\varphi (\underline {n},\bar x):= \exists y (\text {"}y{=}n\text {"}\wedge \varphi (y, \bar x))$
; we understand
$\varphi (\underline {n},\bar x):= \exists y (\text {"}y{=}n\text {"}\wedge \varphi (y, \bar x))$
; we understand
![]() $\varphi ^{<z}(\underline {n}, \bar x)$
as
$\varphi ^{<z}(\underline {n}, \bar x)$
as
![]() $\big (\varphi (\underline {n}, \bar x)\big )^{<z}$
. If
$\big (\varphi (\underline {n}, \bar x)\big )^{<z}$
. If
![]() $n<m$
, then both
$n<m$
, then both
![]() $(\text {"}x{=}n\text {"})^{<m}$
and
$(\text {"}x{=}n\text {"})^{<m}$
and
![]() $\text {"}x{=}n\text {"}$
define n in
$\text {"}x{=}n\text {"}$
define n in
![]() $\mathbb {N}$
, so
$\mathbb {N}$
, so
![]() $\varphi ^{<m}(\underline {n}, \bar x)$
and
$\varphi ^{<m}(\underline {n}, \bar x)$
and
![]() $\varphi ^{<m}(n, \bar x)$
are equivalent in
$\varphi ^{<m}(n, \bar x)$
are equivalent in
![]() $\mathbb {N}$
. In particular, for every
$\mathbb {N}$
. In particular, for every
![]() $n\in \mathbb {N}$
:
$n\in \mathbb {N}$
:
Proof of Theorem 1.4
For contradiction, assume otherwise, so ![]() by Lemma 4.1. By Corollary 2.7, there is an increasing computable function
by Lemma 4.1. By Corollary 2.7, there is an increasing computable function
![]() $h: \mathbb {N}\to \mathbb {N}$
and a sentence
$h: \mathbb {N}\to \mathbb {N}$
and a sentence
![]() $\textit {sat}$
such that for every
$\textit {sat}$
such that for every
![]() $n\in \mathbb {N}$
and every
$n\in \mathbb {N}$
and every
![]() $L^{\text {r}}_{\text {ar}}$
-sentence
$L^{\text {r}}_{\text {ar}}$
-sentence
![]() $\varphi $
with
$\varphi $
with
![]() $n> h(\mathit {num}(\varphi ))$
we have
$n> h(\mathit {num}(\varphi ))$
we have
For
![]() $k<n$
, let
$k<n$
, let
![]() $(n,k)$
denote the expansion of the standard
$(n,k)$
denote the expansion of the standard
![]() $L^{\text {r}}_{\text {ar}}$
-structure n that interprets a constant c by k. It is clear that there is an interpretation
$L^{\text {r}}_{\text {ar}}$
-structure n that interprets a constant c by k. It is clear that there is an interpretation
![]() ${\mathit I} $
(independent of
${\mathit I} $
(independent of
![]() $n, \varphi $
) such that
$n, \varphi $
) such that
![]() $(n,\mathit {num}(\varphi ))^{{\mathit I}}\cong {\mathcal S}( \langle 1^n, \varphi \rangle )$
for all
$(n,\mathit {num}(\varphi ))^{{\mathit I}}\cong {\mathcal S}( \langle 1^n, \varphi \rangle )$
for all
![]() $\varphi $
with
$\varphi $
with
![]() $\mathit {num}(\varphi )<n$
. Replacing in
$\mathit {num}(\varphi )<n$
. Replacing in
![]() $\textit {sat}^{{\mathit I}}$
the constant c by a new variable x gives an
$\textit {sat}^{{\mathit I}}$
the constant c by a new variable x gives an
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\textit {true}(x)$
such that for
$\textit {true}(x)$
such that for
![]() $n> h(\mathit {num}(\varphi ))\geqslant \mathit {num}(\varphi )$
:
$n> h(\mathit {num}(\varphi ))\geqslant \mathit {num}(\varphi )$
:
 $$ \begin{align} {\mathcal S}\big(\langle 1^n, \varphi\rangle\big) \models \textit{sat} & \iff n \models \textit{true}\big(\mathit{num}(\varphi)\big)\nonumber \\ & \iff \mathbb{N}\models \textit{true}^{<n}\big(\mathit{num}(\varphi)\big), \end{align} $$
$$ \begin{align} {\mathcal S}\big(\langle 1^n, \varphi\rangle\big) \models \textit{sat} & \iff n \models \textit{true}\big(\mathit{num}(\varphi)\big)\nonumber \\ & \iff \mathbb{N}\models \textit{true}^{<n}\big(\mathit{num}(\varphi)\big), \end{align} $$
where
![]() $\mathbb {N}$
is the standard
$\mathbb {N}$
is the standard
![]() $L^{\text {r}}_{\text {ar}}$
-model. Since
$L^{\text {r}}_{\text {ar}}$
-model. Since
![]() $h: \mathbb {N}\to \mathbb {N}$
is computable, there is an
$h: \mathbb {N}\to \mathbb {N}$
is computable, there is an
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\text {"} h(x)< y\text {"}$
with the obvious meaning. Note the l.h.s. of (5) is equivalent to
$\text {"} h(x)< y\text {"}$
with the obvious meaning. Note the l.h.s. of (5) is equivalent to
![]() $\mathbb {N}\models \varphi ^{<n}$
. Combining (5) and (6) we get that
$\mathbb {N}\models \varphi ^{<n}$
. Combining (5) and (6) we get that
![]() $\mathbb {N}$
satisfies the universal closure of
$\mathbb {N}$
satisfies the universal closure of
for every
![]() $L^{\text {r}}_{\text {ar}}$
-sentence
$L^{\text {r}}_{\text {ar}}$
-sentence
![]() $\varphi $
. But
$\varphi $
. But
![]() $M\models \text {"} h(\mathit {num}(\varphi ))<a\text {"}$
, hence
$M\models \text {"} h(\mathit {num}(\varphi ))<a\text {"}$
, hence
for every
![]() $L^{\text {r}}_{\text {ar}}$
-sentence
$L^{\text {r}}_{\text {ar}}$
-sentence
![]() $\varphi $
. As stated in [Reference Paris and Dimitracopoulos34, proof of Proposition 3] this contradicts Tarski’s undefinability of truth. We include the details as they are omitted in [Reference Paris and Dimitracopoulos34].
$\varphi $
. As stated in [Reference Paris and Dimitracopoulos34, proof of Proposition 3] this contradicts Tarski’s undefinability of truth. We include the details as they are omitted in [Reference Paris and Dimitracopoulos34].
The function which for every
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\varphi (x)$
maps
$\varphi (x)$
maps
![]() $\mathit {num}(\varphi )$
to
$\mathit {num}(\varphi )$
to
![]() $\mathit {num}(\varphi (\underline {\mathit {num}(\varphi )}))$
is computable. So by Lemma 4.2, there is a formula
$\mathit {num}(\varphi (\underline {\mathit {num}(\varphi )}))$
is computable. So by Lemma 4.2, there is a formula
![]() $\textit {sub}(x,y)$
such that for every formula
$\textit {sub}(x,y)$
such that for every formula
![]() $\varphi (x)$
and every
$\varphi (x)$
and every
![]() $b\in M$
:
$b\in M$
:
Define
![]() $\chi (x) := \forall y\big (\textit {sub}(x,y) \to \neg \textit {true}(y))$
and
$\chi (x) := \forall y\big (\textit {sub}(x,y) \to \neg \textit {true}(y))$
and
![]() $\theta :=\chi (\underline {\mathit {num}(\chi )})$
, and note
$\theta :=\chi (\underline {\mathit {num}(\chi )})$
, and note
We arrive at the desired contradiction:
 $$\begin{align*}\!\!\!\!\!\!\!\begin{array}{@{}lrll} & M \models \theta^{<a} \iff & M\models \forall y{<}a \big(\textit{sub}^{<a}(\mathit{num}(\chi),y)\to \neg \textit{true}^{<a}(y)\big) & \text{by (}{4}\text{)} \\ & \iff &\text{for all } b<^M a: M \models \textit{sub}^{<a}(\mathit{num}(\chi),b) \to \neg \textit{true}^{<a}(b) \\ & \iff & M\models \neg \textit{true}^{<a}(\mathit{num}(\theta)) & \text{by (}{8}\text{) and (}{9}\text{)} \\ & \iff & M\not\models \theta^{<a} & \text{by (}{7}\text{)}. \end{array} \end{align*}$$
$$\begin{align*}\!\!\!\!\!\!\!\begin{array}{@{}lrll} & M \models \theta^{<a} \iff & M\models \forall y{<}a \big(\textit{sub}^{<a}(\mathit{num}(\chi),y)\to \neg \textit{true}^{<a}(y)\big) & \text{by (}{4}\text{)} \\ & \iff &\text{for all } b<^M a: M \models \textit{sub}^{<a}(\mathit{num}(\chi),b) \to \neg \textit{true}^{<a}(b) \\ & \iff & M\models \neg \textit{true}^{<a}(\mathit{num}(\theta)) & \text{by (}{8}\text{) and (}{9}\text{)} \\ & \iff & M\not\models \theta^{<a} & \text{by (}{7}\text{)}. \end{array} \end{align*}$$
4.3 Upper bounds
Based on our analysis of halting problems in Section 3, we now see that various upper bounds on the complexity of ![]() imply separations of classical complexity classes from
imply separations of classical complexity classes from
![]() $\mathsf {LINH}$
. This is our main result. The first assertion is Theorem 1.3:
$\mathsf {LINH}$
. This is our main result. The first assertion is Theorem 1.3:
Theorem 4.3.
-
(i) If
 , then
, then
 $\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
$\mathsf {NE}\not \subseteq \mathsf {LINH}$
. -
(ii) If
 , then
, then
 $\mathsf {E}\not \subseteq \mathsf {LINH}$
.
$\mathsf {E}\not \subseteq \mathsf {LINH}$
. -
(iii) If
 , then
, then
 $\mathsf {NLINSPACE}\not \subseteq \mathsf {LINH}$
.
$\mathsf {NLINSPACE}\not \subseteq \mathsf {LINH}$
. -
(iv) If
 , then
, then
 $\mathsf {LINSPACE}\not \subseteq \mathsf {LINH}$
.
$\mathsf {LINSPACE}\not \subseteq \mathsf {LINH}$
.
5 Provability of the MRDP theorem
In this section we prove:
Theorem 1.5. If
![]() $I\Delta _0$
proves MRDP for small numbers, then
$I\Delta _0$
proves MRDP for small numbers, then
![]() $\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
$\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
In fact, we show that Theorem 1.3 implies a stronger statement for all computably enumerable
![]() $\Pi _1$
-theories—up to logical equivalence,
$\Pi _1$
-theories—up to logical equivalence,
![]() $I\Delta _0$
is a
$I\Delta _0$
is a
![]() $\Pi _1$
-theory. Here, a theory is a set of sentences, and a
$\Pi _1$
-theory. Here, a theory is a set of sentences, and a
![]() $\Pi _1$
-theory is a set of
$\Pi _1$
-theory is a set of
![]() $\Pi _1$
-sentences. The proof uses Parikh’s theorem [Reference Parikh33]:
$\Pi _1$
-sentences. The proof uses Parikh’s theorem [Reference Parikh33]:
Theorem 5.1. Let T be a
![]() $\Pi _1$
-theory and
$\Pi _1$
-theory and
![]() $\varphi (\bar x, \bar y)$
a
$\varphi (\bar x, \bar y)$
a
![]() $\Delta _0$
-formula. If T proves
$\Delta _0$
-formula. If T proves
![]() $\exists \bar y\; \varphi (\bar x, \bar y)$
, then T proves
$\exists \bar y\; \varphi (\bar x, \bar y)$
, then T proves
![]() $\exists \bar y{<}p(\bar x)\; \varphi (\bar x, \bar y) $
for some term
$\exists \bar y{<}p(\bar x)\; \varphi (\bar x, \bar y) $
for some term
![]() $p(\bar x)$
.
$p(\bar x)$
.
Definition 5.2. A theory T proves MRDP if for every
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (\bar x)$
there are
$\varphi (\bar x)$
there are
![]() $L_{\text {ar}}$
-terms
$L_{\text {ar}}$
-terms
![]() $p(\bar x, \bar y)$
and
$p(\bar x, \bar y)$
and
![]() $q(\bar x, \bar y)$
such that T proves
$q(\bar x, \bar y)$
such that T proves
As mentioned in the introduction it is a long standing open problem whether
![]() $I\Delta _0$
proves MRDP and it is known that adding exponentiation suffices. Intuitively, the following concept asks whether MRDP can be proved using exponentiation only once.
$I\Delta _0$
proves MRDP and it is known that adding exponentiation suffices. Intuitively, the following concept asks whether MRDP can be proved using exponentiation only once.
Definition 5.3. A theory T proves MRDP for small numbers if for every
![]() $k\in \mathbb {N}$
and every
$k\in \mathbb {N}$
and every
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (\bar x)= \varphi (x_0, \ldots , x_{k-1})$
there are
$\varphi (\bar x)= \varphi (x_0, \ldots , x_{k-1})$
there are
![]() $L_{\text {ar}}$
-terms
$L_{\text {ar}}$
-terms
![]() $p(\bar x, \bar y)$
and
$p(\bar x, \bar y)$
and
![]() $q(\bar x, \bar y)$
such that T proves
$q(\bar x, \bar y)$
such that T proves
Here,
![]() $2^x{\leqslant }z$
stands for a well-known
$2^x{\leqslant }z$
stands for a well-known
![]() $\Delta _0$
-formula [Reference Hájek and Pudlák25, Section V.3(c)]. The following strengthens Theorem 1.5:
$\Delta _0$
-formula [Reference Hájek and Pudlák25, Section V.3(c)]. The following strengthens Theorem 1.5:
Theorem 5.4. Let T be a true
![]() $\Pi _1$
-theory. Moreover, assume that T is computably enumerable. If T proves MRDP for small numbers, then
$\Pi _1$
-theory. Moreover, assume that T is computably enumerable. If T proves MRDP for small numbers, then ![]() and thus
and thus
![]() $\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
$\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
Proof Assume T proves (10) for
![]() $\varphi (x)$
, and hence
$\varphi (x)$
, and hence
By Theorem 5.1
![]() $\exists \bar y$
can be replaced by
$\exists \bar y$
can be replaced by
![]() $\exists \bar y{<}r(x,z)$
for some term
$\exists \bar y{<}r(x,z)$
for some term
![]() $r(x,z)$
. But since T proves (10) for
$r(x,z)$
. But since T proves (10) for
![]() $\varphi (x)$
, T proves
$\varphi (x)$
, T proves
Since T is computably enumerable, such terms
![]() $p,q,r$
can be computed from
$p,q,r$
can be computed from
![]() $\varphi $
. Given an instance
$\varphi $
. Given an instance
![]() $ \langle 1^n,\varphi \rangle $
of
$ \langle 1^n,\varphi \rangle $
of ![]() , compute
, compute
![]() $p,q,r$
as above, guess
$p,q,r$
as above, guess
![]() $\bar m<r(n,2^n)$
and check
$\bar m<r(n,2^n)$
and check
![]() $p(n, \bar m){=} q(n, \bar m)$
. Note the length of the guess
$p(n, \bar m){=} q(n, \bar m)$
. Note the length of the guess
![]() $\bar m$
is
$\bar m$
is
![]() $O(|r|\cdot \ell \cdot n)$
where
$O(|r|\cdot \ell \cdot n)$
where
![]() $\ell $
is the length of the tuple
$\ell $
is the length of the tuple
![]() $\bar y$
. The check can be done in time
$\bar y$
. The check can be done in time
![]() $(|p|\cdot |q|\cdot |r|\cdot n)^{O(1)}$
.
$(|p|\cdot |q|\cdot |r|\cdot n)^{O(1)}$
.
It follows that ![]() . Now apply Theorem 1.3.
. Now apply Theorem 1.3.
It would be interesting to find variants of this result that infer ![]() or
or ![]() from certain provabilities of MRDP or other arithmetical statements. Note this implies stronger separations of complexity classes by Theorem 4.3.
from certain provabilities of MRDP or other arithmetical statements. Note this implies stronger separations of complexity classes by Theorem 4.3.
6 p-Halt and a universal
 $\mathsf {AC}^0$
-easy set in
$\mathsf {AC}^0$
-easy set in
 $\mathsf {NP}$
$\mathsf {NP}$
Recall, a problem Q is
![]() $\mathsf {AC}^0$
-bi-immune if neither Q nor its complement contain an infinite subset in
$\mathsf {AC}^0$
-bi-immune if neither Q nor its complement contain an infinite subset in
![]() $\mathsf {AC}^0$
. In this section we prove the following.
$\mathsf {AC}^0$
. In this section we prove the following.
Theorem 1.6. If
![]() $\mathsf {NP}$
contains an
$\mathsf {NP}$
contains an
![]() $\mathsf {AC}^0$
-bi-immune problem, then
$\mathsf {AC}^0$
-bi-immune problem, then ![]() .
.
We use the following technical lemma stating, roughly, that every computable function is dominated by a computable injection which is
![]() $\mathsf {AC}^0$
-invertible.
$\mathsf {AC}^0$
-invertible.
Lemma 6.1. Let
![]() $f: \mathbb {N}\to \mathbb {N}$
be computable. Then there is an increasing
$f: \mathbb {N}\to \mathbb {N}$
be computable. Then there is an increasing
![]() $h: \mathbb {N}\to \mathbb {N}$
with the following properties.
$h: \mathbb {N}\to \mathbb {N}$
with the following properties.
-
(i)
 $h(n)\geqslant f(n^2)$
for every
$h(n)\geqslant f(n^2)$
for every
 $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
. -
(ii)
 $1^n\mapsto 1^{h(n)}$
is computable in time
$1^n\mapsto 1^{h(n)}$
is computable in time
 $h(n)^{O(1)}$
.
$h(n)^{O(1)}$
. -
(iii) There is an
 $L^{\text {r}}_{\text {ar}}$
-sentence
$L^{\text {r}}_{\text {ar}}$
-sentence
 $\varphi _h$
such that for every
$\varphi _h$
such that for every
 $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
 $|x|>1$
:
$|x|>1$
:  $$ \begin{align*} {\mathcal S}(x)\models\varphi_h & \iff x= 1^{h(n)} \text{ for some } n\in \mathbb{N}. \end{align*} $$
$$ \begin{align*} {\mathcal S}(x)\models\varphi_h & \iff x= 1^{h(n)} \text{ for some } n\in \mathbb{N}. \end{align*} $$
-
(iv) There is an
 $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
 $\varphi (x)$
that defines n in
$\varphi (x)$
that defines n in
 $ {\mathcal S}(1^{h(n)})$
for every
$ {\mathcal S}(1^{h(n)})$
for every
 $n>1$
.
$n>1$
.
Proof Given a deterministic Turing machine
![]() $\mathbb M$
and
$\mathbb M$
and
![]() $x\in \{0,1\}^*$
we let
$x\in \{0,1\}^*$
we let
![]() $y_{\mathbb M, x}\in \{0,1\}^*$
encode the computation of
$y_{\mathbb M, x}\in \{0,1\}^*$
encode the computation of
![]() $\mathbb M$
on x. This encoding can be chosen so that:
$\mathbb M$
on x. This encoding can be chosen so that:
-
(a)
 $x\mapsto y_{\mathbb M, x}$
is computable in time
$x\mapsto y_{\mathbb M, x}$
is computable in time
 $|y_{\mathbb M, x}|^{O(1)}$
.
$|y_{\mathbb M, x}|^{O(1)}$
. -
(b)
 $\big \{ \langle x, y_{\mathbb M, x} \rangle \;\big |\; x\in \{0,1\}^*\big \}\in \mathsf {AC}^0$
.
$\big \{ \langle x, y_{\mathbb M, x} \rangle \;\big |\; x\in \{0,1\}^*\big \}\in \mathsf {AC}^0$
.
Now, let
![]() $\mathbb M_f$
be a Turing machine that computes
$\mathbb M_f$
be a Turing machine that computes
![]() $1^n\mapsto 1^{f(n)}$
. Let
$1^n\mapsto 1^{f(n)}$
. Let
![]() $\mathbb M$
be the machine that on input
$\mathbb M$
be the machine that on input
![]() $1^n$
runs
$1^n$
runs
![]() $\mathbb M_f$
on
$\mathbb M_f$
on
![]() $1^{i^2}$
for every
$1^{i^2}$
for every
![]() $i\leqslant n$
. Define the increasing function
$i\leqslant n$
. Define the increasing function
![]() $h:\mathbb {N}\to \mathbb {N}$
by
$h:\mathbb {N}\to \mathbb {N}$
by
Clearly, the string
![]() $y_{\mathbb M_f, 1^{n^2}}$
encoding the computation of
$y_{\mathbb M_f, 1^{n^2}}$
encoding the computation of
![]() $\mathbb M_f$
on input
$\mathbb M_f$
on input
![]() $1^{n^2}$
has length at least
$1^{n^2}$
has length at least
![]() $f(n^2)$
. Similarly,
$f(n^2)$
. Similarly,
![]() $|y_{\mathbb M, 1^n}|\geqslant f(n^2)$
. Thus
$|y_{\mathbb M, 1^n}|\geqslant f(n^2)$
. Thus
![]() $h(n)\geqslant f(n^2)$
for every
$h(n)\geqslant f(n^2)$
for every
![]() $n\in \mathbb {N}$
, i.e., (i) holds.
$n\in \mathbb {N}$
, i.e., (i) holds.
(ii) holds by (a). To show (iii), Theorem 2.6 and (b) imply that there is an
![]() $L^{\text {r}}_{\text {ar}}$
-sentence
$L^{\text {r}}_{\text {ar}}$
-sentence
![]() $\varphi $
that holds precisely in the string structures of the form
$\varphi $
that holds precisely in the string structures of the form
![]() ${\mathcal S}\big (\mathit {bin}(h(n))\big )$
for
${\mathcal S}\big (\mathit {bin}(h(n))\big )$
for
![]() $n\in \mathbb {N}$
. Using
$n\in \mathbb {N}$
. Using
![]() $\mathit {BIT}$
, there is an interpretation
$\mathit {BIT}$
, there is an interpretation
![]() ${\mathit I} $
such that
${\mathit I} $
such that
![]() $\mathcal S(1^m)^{{\mathit I}}\cong {\mathcal S}(\mathit {bin}(m))$
for every
$\mathcal S(1^m)^{{\mathit I}}\cong {\mathcal S}(\mathit {bin}(m))$
for every
![]() $m> 1$
, so
$m> 1$
, so
![]() $\varphi _h:= \varphi ^{{\mathit I}}$
holds precisely in the string structures of the form
$\varphi _h:= \varphi ^{{\mathit I}}$
holds precisely in the string structures of the form
![]() ${\mathcal S}(1^{h(n)})$
for
${\mathcal S}(1^{h(n)})$
for
![]() $n\in \mathbb {N}$
(we have
$n\in \mathbb {N}$
(we have
![]() $h(n)>1$
for all
$h(n)>1$
for all
![]() $n\in \mathbb {N}$
).
$n\in \mathbb {N}$
).
Trivially, n is definable in
![]() ${\mathcal S}(\mathit {bin}(h(n)))$
, so (iv) follows using the interpretation I above.
${\mathcal S}(\mathit {bin}(h(n)))$
, so (iv) follows using the interpretation I above.
Theorem 1.6 is an easy consequence of the following stronger result, and we view it as good evidence for the truth of Conjecture 1.1.
Theorem 6.2. Assume ![]() . Then there is an infinite tally problem X such that for every
. Then there is an infinite tally problem X such that for every
![]() $Q\in \mathsf {NP}$
we have
$Q\in \mathsf {NP}$
we have
![]() $Q\cap X\in \mathsf {AC}^0$
.
$Q\cap X\in \mathsf {AC}^0$
.
Proof of Theorem 1.6 from Theorem 6.2: Assume ![]() and let
and let
![]() $Q\in \mathsf {NP}$
. Let X be as stated in Theorem 6.2. Then either
$Q\in \mathsf {NP}$
. Let X be as stated in Theorem 6.2. Then either
![]() $Q\cap X$
or
$Q\cap X$
or
![]() $(\{0,1\}^*\setminus Q)\cap X$
is infinite. By Theorem 6.2 they are both in
$(\{0,1\}^*\setminus Q)\cap X$
is infinite. By Theorem 6.2 they are both in
![]() $\mathsf {AC}^0$
; indeed,
$\mathsf {AC}^0$
; indeed,
![]() $(\{0,1\}^*\setminus Q)\cap X=(\{0,1\}^*\cap X)\setminus (Q\cap X) $
is in
$(\{0,1\}^*\setminus Q)\cap X=(\{0,1\}^*\cap X)\setminus (Q\cap X) $
is in
![]() $\mathsf {AC}^0$
because both
$\mathsf {AC}^0$
because both
![]() $\{0,1\}^*\cap X$
and
$\{0,1\}^*\cap X$
and
![]() $Q\cap X$
are. Hence, Q is not
$Q\cap X$
are. Hence, Q is not
![]() $\mathsf {AC}^0$
-bi-immune.
$\mathsf {AC}^0$
-bi-immune.
Proof of Theorem 6.2
By Corollary 2.7 there is a computable increasing function
![]() $f:\mathbb {N}\to \mathbb {N}$
and an
$f:\mathbb {N}\to \mathbb {N}$
and an
![]() $L^{\text {r}}_{\text {ar}}$
-sentence
$L^{\text {r}}_{\text {ar}}$
-sentence
![]() $\varphi $
such that for every
$\varphi $
such that for every
![]() $ \langle 1^n, \mathbb M \rangle $
with
$ \langle 1^n, \mathbb M \rangle $
with
![]() $n \geqslant f(|\mathbb M|)$
:
$n \geqslant f(|\mathbb M|)$
:
Now let
![]() $h: \mathbb {N}\to \mathbb {N}$
be the increasing function as stated in Lemma 6.1. In particular, there is a deterministic Turing machine
$h: \mathbb {N}\to \mathbb {N}$
be the increasing function as stated in Lemma 6.1. In particular, there is a deterministic Turing machine
![]() $\mathbb M_h$
and a constant
$\mathbb M_h$
and a constant
![]() $c\geqslant 1$
such that on input
$c\geqslant 1$
such that on input
![]() $1^m$
the machine
$1^m$
the machine
![]() $\mathbb M_h$
outputs the string
$\mathbb M_h$
outputs the string
![]() $1^{h(m)}$
in time
$1^{h(m)}$
in time
![]() $h(m)^c$
. The desired set X is defined by
$h(m)^c$
. The desired set X is defined by
By Lemma 6.1(iii) the sentence
![]() $\varphi _h$
witnesses
$\varphi _h$
witnesses
![]() $X\in \mathsf {AC}^0$
according to Theorem 2.6.
$X\in \mathsf {AC}^0$
according to Theorem 2.6.
Now let
![]() $Q\subseteq \{0,1\}^*$
be a problem in
$Q\subseteq \{0,1\}^*$
be a problem in
![]() $\mathsf {NP}$
. In particular, there is a nondeterministic Turing machine
$\mathsf {NP}$
. In particular, there is a nondeterministic Turing machine
![]() $\mathbb M_Q$
accepting Q and a constant
$\mathbb M_Q$
accepting Q and a constant
![]() $d\geqslant 1$
such that
$d\geqslant 1$
such that
![]() $\mathbb M_Q$
on x runs in time
$\mathbb M_Q$
on x runs in time
![]() $|x|^d$
.
$|x|^d$
.
Define the nondeterministic Turing machine
![]() $\mathbb M_{Q,h,m}$
to run
$\mathbb M_{Q,h,m}$
to run
![]() $\mathbb M_h$
on
$\mathbb M_h$
on
![]() $1^m$
to produce output
$1^m$
to produce output
![]() $1^{h(m)}$
and then run
$1^{h(m)}$
and then run
![]() $\mathbb M_Q$
on
$\mathbb M_Q$
on
![]() $1^{h(m)}$
. This machine runs in time
$1^{h(m)}$
. This machine runs in time
Choose a constant
![]() $e\in \mathbb {N}$
such that
$e\in \mathbb {N}$
such that
![]() $m\geqslant |\mathbb M_h|+ |\mathbb M_Q|+ e$
implies
$m\geqslant |\mathbb M_h|+ |\mathbb M_Q|+ e$
implies
![]() $m^2\geqslant |\mathbb M_{Q,h,m}|$
. Then
$m^2\geqslant |\mathbb M_{Q,h,m}|$
. Then
Hence, by (12), for
![]() $m\geqslant |\mathbb M_h|+ |\mathbb M_Q|+e$
:
$m\geqslant |\mathbb M_h|+ |\mathbb M_Q|+e$
:
 $$ \begin{align} 1^{h(m)}\in Q & \iff {\mathbb M}_{Q,h,m} \text{ accepts the empty input in at most } n(m) \text{ steps}\notag \\ & \iff {\mathcal S}(\langle 1^{n(m)},\mathbb M_{Q,h,m}\rangle)\models \varphi. \end{align} $$
$$ \begin{align} 1^{h(m)}\in Q & \iff {\mathbb M}_{Q,h,m} \text{ accepts the empty input in at most } n(m) \text{ steps}\notag \\ & \iff {\mathcal S}(\langle 1^{n(m)},\mathbb M_{Q,h,m}\rangle)\models \varphi. \end{align} $$
Lemma 6.1(iv) implies that there is an interpretation
![]() ${\mathit I} $
such that for every
${\mathit I} $
such that for every
![]() $m\in \mathbb {N}$
$m\in \mathbb {N}$
By Theorem 2.6 it suffices to show that for every
![]() $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
![]() $|x|\geqslant h(|\mathbb M_h|+ |\mathbb M_Q|+ e)$
:
$|x|\geqslant h(|\mathbb M_h|+ |\mathbb M_Q|+ e)$
:
Assume
![]() $x\in Q\cap X$
. Then
$x\in Q\cap X$
. Then
![]() $x=1^{h(m)}$
for some
$x=1^{h(m)}$
for some
![]() $m>1$
and
$m>1$
and
![]() $\mathcal S(x)\models \varphi _h$
. Since
$\mathcal S(x)\models \varphi _h$
. Since
![]() $|x|=h(m)\geqslant h(|\mathbb M_h|+ |\mathbb M_Q|+e)$
and h is increasing, we have
$|x|=h(m)\geqslant h(|\mathbb M_h|+ |\mathbb M_Q|+e)$
and h is increasing, we have
![]() $m\geqslant |\mathbb M_h|+ |\mathbb M_Q|+e$
. Thus
$m\geqslant |\mathbb M_h|+ |\mathbb M_Q|+e$
. Thus
![]() $x=1^{h(m)}\in Q$
implies
$x=1^{h(m)}\in Q$
implies
![]() ${\mathcal S}( \langle 1^{n(m)}, \mathbb M_{Q,h,m} \rangle )\models \varphi $
by (13), and
${\mathcal S}( \langle 1^{n(m)}, \mathbb M_{Q,h,m} \rangle )\models \varphi $
by (13), and
![]() ${\mathcal S}(1^{h(m)})\models \varphi ^{{\mathit I}}$
follows.
${\mathcal S}(1^{h(m)})\models \varphi ^{{\mathit I}}$
follows.
Conversely, assume
![]() $S(x)\models \varphi _h\wedge \varphi ^{{\mathit I}}$
. By
$S(x)\models \varphi _h\wedge \varphi ^{{\mathit I}}$
. By
![]() $\mathcal S(x)\models \varphi _h$
, we have
$\mathcal S(x)\models \varphi _h$
, we have
![]() $x\in X$
, so
$x\in X$
, so
![]() $x=1^{h(m)}$
for some
$x=1^{h(m)}$
for some
![]() $m>1$
. By
$m>1$
. By
![]() ${\mathcal S}(1^{h(m)})\models \varphi ^{{\mathit I}}$
we have
${\mathcal S}(1^{h(m)})\models \varphi ^{{\mathit I}}$
we have
![]() ${\mathcal S}( \langle 1^{n(m)}, \mathbb M_{Q,h,m} \rangle )\models \varphi $
. This implies
${\mathcal S}( \langle 1^{n(m)}, \mathbb M_{Q,h,m} \rangle )\models \varphi $
. This implies
![]() $x=1^{h(m)}\in Q$
by (13) because, as above,
$x=1^{h(m)}\in Q$
by (13) because, as above,
![]() $m\geqslant |\mathbb M_h|+ |\mathbb M_Q|+e$
.
$m\geqslant |\mathbb M_h|+ |\mathbb M_Q|+e$
.
7 Problem comparison
7.1 The role of uniformity
Our proof of the lower bound ![]() (Theorem 1.4) makes crucial use of the uniformity condition in the definition of
(Theorem 1.4) makes crucial use of the uniformity condition in the definition of
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
. To shed some light on this dependence, we relax the uniformity condition as follows.
$\mathsf {para}\text {-}\mathsf {AC}^0$
. To shed some light on this dependence, we relax the uniformity condition as follows.
Definition 7.1. Let
![]() $(Q,\kappa )$
be a parameterized problem and
$(Q,\kappa )$
be a parameterized problem and
![]() $d,k\in \mathbb {N}$
. The kth slice of
$d,k\in \mathbb {N}$
. The kth slice of
![]() $(Q,\kappa )$
is the classical problem
$(Q,\kappa )$
is the classical problem
![]() $\{x\in Q\mid \kappa (x)=k\}$
. The class
$\{x\in Q\mid \kappa (x)=k\}$
. The class
![]() ${\mathsf {XAC}^0}$
contains
${\mathsf {XAC}^0}$
contains
![]() $(Q,\kappa )$
if and only if
$(Q,\kappa )$
if and only if
![]() $\mathsf {AC}^0$
contains every slice of
$\mathsf {AC}^0$
contains every slice of
![]() $(Q,\kappa )$
. The class
$(Q,\kappa )$
. The class
![]() ${\mathsf {XAC}^0_{d}}$
contains
${\mathsf {XAC}^0_{d}}$
contains
![]() $(Q,\kappa )$
if and only if
$(Q,\kappa )$
if and only if
![]() ${\mathsf {AC}^0_{d}}$
contains every slice of
${\mathsf {AC}^0_{d}}$
contains every slice of
![]() $(Q,\kappa )$
; here,
$(Q,\kappa )$
; here,
![]() ${\mathsf {AC}^0_{d}}$
denotes the class of problems decided by dlogtime uniform circuit families of polynomial size and depth d.
${\mathsf {AC}^0_{d}}$
denotes the class of problems decided by dlogtime uniform circuit families of polynomial size and depth d.
Clearly,
and
![]() ${\mathsf {XAC}^0_{0}} \not \subseteq \mathsf {para}\text {-}\mathsf {AC}^0$
since it contains undecidable problems.
${\mathsf {XAC}^0_{0}} \not \subseteq \mathsf {para}\text {-}\mathsf {AC}^0$
since it contains undecidable problems.
Lemma 7.2. Assume there is an eventually definable reduction from
![]() $(Q, \kappa )$
to
$(Q, \kappa )$
to
![]() $(Q', \kappa ')$
.
$(Q', \kappa ')$
.
-
(i) If
 $(Q', \kappa ')\in {\mathsf {XAC}^0}$
, then
$(Q', \kappa ')\in {\mathsf {XAC}^0}$
, then
 $(Q, \kappa )\in {\mathsf {XAC}^0}$
.
$(Q, \kappa )\in {\mathsf {XAC}^0}$
. -
(ii) If
 $(Q', \kappa ')\in \bigcup _d {\mathsf {XAC}^0_{d}}$
, then
$(Q', \kappa ')\in \bigcup _d {\mathsf {XAC}^0_{d}}$
, then
 $(Q, \kappa )\in \bigcup _d {\mathsf {XAC}^0_{d}}$
.
$(Q, \kappa )\in \bigcup _d {\mathsf {XAC}^0_{d}}$
.
Proof Let r denote the reduction and choose f such that
![]() $\kappa '\circ r\leqslant f\circ \kappa $
. Choose an interpretation I and a function h witnessing that r is eventually definable. To show (i), assume
$\kappa '\circ r\leqslant f\circ \kappa $
. Choose an interpretation I and a function h witnessing that r is eventually definable. To show (i), assume
![]() $(Q',\kappa ')\in {\mathsf {XAC}^0}$
. We show that for every
$(Q',\kappa ')\in {\mathsf {XAC}^0}$
. We show that for every
![]() $k\in \mathbb {N}$
the kth slice of Q is in
$k\in \mathbb {N}$
the kth slice of Q is in
![]() $\mathsf {AC}^0$
.
$\mathsf {AC}^0$
.
Fix
![]() $k\in \mathbb {N}$
and let
$k\in \mathbb {N}$
and let
![]() $x\in \{0,1\}^*$
with
$x\in \{0,1\}^*$
with
![]() $\kappa (x)=k$
. Since
$\kappa (x)=k$
. Since
![]() $\kappa '$
is
$\kappa '$
is
![]() $\mathsf {AC}^0$
-computable, Theorem 2.6 implies that for every
$\mathsf {AC}^0$
-computable, Theorem 2.6 implies that for every
![]() $k'\in \mathbb {N}$
there is a sentence
$k'\in \mathbb {N}$
there is a sentence
![]() $\chi _{k'}$
that is true in
$\chi _{k'}$
that is true in
![]() ${\mathcal S}(r(x))$
if and only if
${\mathcal S}(r(x))$
if and only if
![]() $\kappa '(r(x))=k'$
. For every
$\kappa '(r(x))=k'$
. For every
![]() $k'\in \mathbb {N}$
choose a sentence
$k'\in \mathbb {N}$
choose a sentence
![]() $\psi _{k'}$
that defines the
$\psi _{k'}$
that defines the
![]() $k'$
th slice of
$k'$
th slice of
![]() $Q'$
according to Theorem 2.6. If
$Q'$
according to Theorem 2.6. If
![]() $|x|\geqslant h(k)$
, then
$|x|\geqslant h(k)$
, then
is true in
![]() ${\mathcal S}(x)$
if and only if
${\mathcal S}(x)$
if and only if
![]() $r(x)\in Q'$
, i.e.,
$r(x)\in Q'$
, i.e.,
![]() $x\in Q$
. Translating
$x\in Q$
. Translating
![]() $\varphi $
gives an
$\varphi $
gives an
![]() $\mathsf {AC}^0$
-family that decides the kth slice of Q on instances x with
$\mathsf {AC}^0$
-family that decides the kth slice of Q on instances x with
![]() $|x|\geqslant h(k)$
. This can be extended to the whole slice by hardwiring instances of length
$|x|\geqslant h(k)$
. This can be extended to the whole slice by hardwiring instances of length
![]() $<h(k)$
.
$<h(k)$
.
For (ii) we assume there is
![]() $d\in \mathbb {N}$
such that every slice of
$d\in \mathbb {N}$
such that every slice of
![]() $Q'$
is in
$Q'$
is in
![]() $\mathsf {AC}^0_d$
. Now, in Theorem 2.6, the quantifier alternation rank of
$\mathsf {AC}^0_d$
. Now, in Theorem 2.6, the quantifier alternation rank of
![]() $\varphi $
depends only on the depth of the
$\varphi $
depends only on the depth of the
![]() $\mathsf {AC}^0$
-family, and vice-versa; this follows from the proof of [Reference Barrington, Immerman and Straubing6, Theorem 8.1]. In particular, all
$\mathsf {AC}^0$
-family, and vice-versa; this follows from the proof of [Reference Barrington, Immerman and Straubing6, Theorem 8.1]. In particular, all
![]() $\psi _{k'}$
and
$\psi _{k'}$
and
![]() $\chi _{k'}$
have quantifier alternation rank
$\chi _{k'}$
have quantifier alternation rank
![]() $\leqslant d'$
for some
$\leqslant d'$
for some
![]() $d'$
that depends only on d. The depth of the
$d'$
that depends only on d. The depth of the
![]() $\mathsf {AC}^0$
-family translating the above
$\mathsf {AC}^0$
-family translating the above
![]() $\varphi $
is
$\varphi $
is
![]() $\leqslant d"$
for some
$\leqslant d"$
for some
![]() $d"$
depending only on
$d"$
depending only on
![]() $d'$
. The hardwiring of instances of small length can be done by circuits of depth
$d'$
. The hardwiring of instances of small length can be done by circuits of depth
![]() $2$
. Thus,
$2$
. Thus,
![]() $(Q,\kappa )\in {\mathsf {XAC}^0_{d"}}$
.
$(Q,\kappa )\in {\mathsf {XAC}^0_{d"}}$
.
The class
![]() ${\mathsf {XAC}^0}$
is important in our context because it is a natural upper bound on
${\mathsf {XAC}^0}$
is important in our context because it is a natural upper bound on ![]() :
:
Proposition 7.3.
![]() .
.
Proof It suffices to show that for every
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (x)$
the problem
$\varphi (x)$
the problem
![]() $\{1^n\mid \mathbb {N}\models \varphi (n)\}$
belongs to
$\{1^n\mid \mathbb {N}\models \varphi (n)\}$
belongs to
![]() $\mathsf {AC}^0$
. But this problem is
$\mathsf {AC}^0$
. But this problem is
![]() $\mathit {un}(Q)$
for
$\mathit {un}(Q)$
for
![]() $Q:= \{x\in \{0,1\}^*\mid \mathbb {N}\models \varphi (\mathit {num}(x))\}$
. Clearly
$Q:= \{x\in \{0,1\}^*\mid \mathbb {N}\models \varphi (\mathit {num}(x))\}$
. Clearly
![]() $Q\in \mathsf {LINH}$
, so
$Q\in \mathsf {LINH}$
, so
![]() $\mathit {un}(Q)\in \mathsf {AC}^0$
follows from Proposition 2.1.
$\mathit {un}(Q)\in \mathsf {AC}^0$
follows from Proposition 2.1.
We show that it is likely difficult to improve Theorem 1.4 to ![]() . This somewhat artificial class also exhibits the different behaviors of the parameterized problems
. This somewhat artificial class also exhibits the different behaviors of the parameterized problems ![]() ,
, ![]() , and
, and ![]() .
.
Theorem 7.4.
-
(i)
 .
. -
(ii)
 for some
for some
 $d\in \mathbb {N}$
if and only if
$d\in \mathbb {N}$
if and only if
 $\mathsf {NE}\subseteq \mathsf {LINH}$
.
$\mathsf {NE}\subseteq \mathsf {LINH}$
. -
(iii)
 for some
for some
 $d\in \mathbb {N}$
if and only if
$d\in \mathbb {N}$
if and only if
 $\mathsf {LINH}$
collapses.
$\mathsf {LINH}$
collapses.
Proof (i) For fixed
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $\mathbb M_{k,0}, \ldots , \mathbb M_{k,\ell _k-1}$
list all nondeterministic Turing machines of size k and let
$\mathbb M_{k,0}, \ldots , \mathbb M_{k,\ell _k-1}$
list all nondeterministic Turing machines of size k and let
![]() $n_{k,i}$
be the minimal n such that
$n_{k,i}$
be the minimal n such that
![]() $\mathbb M_{k,i}$
accepts the empty input in n steps; if there is no such n, let
$\mathbb M_{k,i}$
accepts the empty input in n steps; if there is no such n, let
![]() $n_{k,i}:=\infty $
. Then, on instances
$n_{k,i}:=\infty $
. Then, on instances
![]() $(1^n,\mathbb M)$
with parameter
$(1^n,\mathbb M)$
with parameter
![]() $|\mathbb M|=k$
,
$|\mathbb M|=k$
, ![]() is decided by the following family of simple Boolean functions:
is decided by the following family of simple Boolean functions:
 $$ \begin{align*} F_{n,k}(& x_0\ldots x_{n-1}, y_0\ldots y_{k-1}) = \bigvee_{\substack{i<\ell_k \text{ such} \\ \text{that } n_{k,i}\leqslant n}}\big(x_0\ldots x_{n-1}= 1^n \wedge y_0\ldots y_{k-1}= \mathbb M_{k,i}\big). \end{align*} $$
$$ \begin{align*} F_{n,k}(& x_0\ldots x_{n-1}, y_0\ldots y_{k-1}) = \bigvee_{\substack{i<\ell_k \text{ such} \\ \text{that } n_{k,i}\leqslant n}}\big(x_0\ldots x_{n-1}= 1^n \wedge y_0\ldots y_{k-1}= \mathbb M_{k,i}\big). \end{align*} $$
Observe that
![]() $F_{n,k}$
can be understood as a circuit of depth
$F_{n,k}$
can be understood as a circuit of depth
![]() $2$
and size
$2$
and size
![]() $O(k\cdot \ell _k\cdot n)$
.
$O(k\cdot \ell _k\cdot n)$
.
(ii) By Remark 3.10,
![]() $\mathsf {NE}\subseteq \mathsf {LINH}$
is equivalent to both
$\mathsf {NE}\subseteq \mathsf {LINH}$
is equivalent to both ![]() and
and ![]() . By (14) it is equivalent to
. By (14) it is equivalent to ![]() .
.
To see (iii), assume
![]() $\mathsf {LINH}$
collapses. Paris and Dimitracopolous [Reference Paris and Dimitracopoulos34, proof of Proposition 4] showed that this implies the following. There is an
$\mathsf {LINH}$
collapses. Paris and Dimitracopolous [Reference Paris and Dimitracopoulos34, proof of Proposition 4] showed that this implies the following. There is an
![]() $L^{\text {r}}_{\text {ar}}$
-formula
$L^{\text {r}}_{\text {ar}}$
-formula
![]() $\lambda (x,y)$
such that for every
$\lambda (x,y)$
such that for every
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (x)$
there are
$\varphi (x)$
there are
![]() $c_\varphi ,d_\varphi ,e_\varphi \in \mathbb {N}$
such that for all
$c_\varphi ,d_\varphi ,e_\varphi \in \mathbb {N}$
such that for all
![]() $n\geqslant c_\varphi $
$n\geqslant c_\varphi $
For each fixed
![]() $\varphi $
there is an
$\varphi $
there is an
![]() $\mathsf {AC}^0$
-family that given
$\mathsf {AC}^0$
-family that given
![]() $1^n$
decides whether n satisfies the r.h.s. The size of this family is bounded by
$1^n$
decides whether n satisfies the r.h.s. The size of this family is bounded by
![]() $n^{f_\varphi }$
for some
$n^{f_\varphi }$
for some
![]() $f_\varphi \in \mathbb {N}$
depending on
$f_\varphi \in \mathbb {N}$
depending on
![]() $\varphi $
, but the depth of this family is determined by the quantifier alternation rank of
$\varphi $
, but the depth of this family is determined by the quantifier alternation rank of
![]() $\lambda $
and, in particular, does not depend on
$\lambda $
and, in particular, does not depend on
![]() $\varphi $
. This implies
$\varphi $
. This implies ![]() for some
for some
![]() $d\in \mathbb {N}$
.
$d\in \mathbb {N}$
.
Conversely, assume ![]() and let
and let
![]() $Q\in \mathsf {LINH}$
. It is well known (see, e.g., [Reference Hájek and Pudlák25, Chapter V, Lemma 2.13]) that there is a
$Q\in \mathsf {LINH}$
. It is well known (see, e.g., [Reference Hájek and Pudlák25, Chapter V, Lemma 2.13]) that there is a
![]() $\Delta _0$
-formula that is satisfied by
$\Delta _0$
-formula that is satisfied by
![]() $\mathit {num}(x)$
if and only if
$\mathit {num}(x)$
if and only if
![]() $x\in Q$
. Fixing this formula in the input to
$x\in Q$
. Fixing this formula in the input to ![]() , the assumption implies that there is a dlogtime uniform circuit family
, the assumption implies that there is a dlogtime uniform circuit family
![]() $(C_{n})_n$
of polynomial size and depth d such that for all
$(C_{n})_n$
of polynomial size and depth d such that for all
![]() $x\in \{0,1\}^*$
:
$x\in \{0,1\}^*$
:
It suffices to show that, given x, the r.h.s. can be checked by an alternating machine in linear time with d alternations. This is straightforward by guessing a path through
![]() $C_{\mathit {num}(x)}$
. For example, if the output gate is a
$C_{\mathit {num}(x)}$
. For example, if the output gate is a
![]() $\vee $
-gate, the machine existentially guesses an input gate
$\vee $
-gate, the machine existentially guesses an input gate
![]() $g_1$
to it, and if it is a
$g_1$
to it, and if it is a
![]() $\wedge $
-gate it universally guesses
$\wedge $
-gate it universally guesses
![]() $g_1$
. Depending on the type of
$g_1$
. Depending on the type of
![]() $g_1$
it either existentially or universally guesses an input gate
$g_1$
it either existentially or universally guesses an input gate
![]() $g_2$
to
$g_2$
to
![]() $g_1$
, and so on. When reaching (with
$g_1$
, and so on. When reaching (with
![]() $g_{d-1}$
or earlier) an input gate or a negation thereof, the machine accepts or rejects, respectively. Each guess requires
$g_{d-1}$
or earlier) an input gate or a negation thereof, the machine accepts or rejects, respectively. Each guess requires
![]() $O(|x|)$
bits. Checking that, e.g.,
$O(|x|)$
bits. Checking that, e.g.,
![]() $g_2$
is an input to
$g_2$
is an input to
![]() $g_1$
can be done in time logarithmic in the size of
$g_1$
can be done in time logarithmic in the size of
![]() $C_{\mathit {num}(x)}$
, that is, in time
$C_{\mathit {num}(x)}$
, that is, in time
![]() $O(|x|)$
. We omit further details.
$O(|x|)$
. We omit further details.
7.2 Reducibilities
On the one hand ![]() might appear ‘easier’ than
might appear ‘easier’ than ![]() in that the latter is not in
in that the latter is not in
![]() $\mathsf {para}\text {-}\mathsf {AC}^0$
while this is unknown for the former. On the other hand, Theorem 7.4 might indicate that
$\mathsf {para}\text {-}\mathsf {AC}^0$
while this is unknown for the former. On the other hand, Theorem 7.4 might indicate that ![]() is ‘harder’ than
is ‘harder’ than ![]() . Also recall from the introduction that
. Also recall from the introduction that ![]() is trivially in
is trivially in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
but not known to be solvable in time
$\mathsf {para}\text {-}\mathsf {NP}$
but not known to be solvable in time
![]() $n^{f(k)}$
while for
$n^{f(k)}$
while for ![]() it is the other way around. The problems seem incomparable. In this subsection we verify this intuition for our notion of reducibility.
it is the other way around. The problems seem incomparable. In this subsection we verify this intuition for our notion of reducibility.
Saying that a (parameterized) problem is reducible to another means that there is an eventually definable reduction. Two problems are equivalent if they are reducible to one another. The picture is as follows: an arrow indicates reducibility,
![]() $\equiv $
means equivalence.
$\equiv $
means equivalence.

In particular, we show unconditionally that ![]() and
and ![]() are not equivalent and both are reducible to yet another almost tally problem of central importance to mathematical logic, namely the following parameterized version of the spectrum problem:
are not equivalent and both are reducible to yet another almost tally problem of central importance to mathematical logic, namely the following parameterized version of the spectrum problem:

Recall that having a model of size n means that n belongs to the spectrum of
![]() $\varphi $
.
$\varphi $
.
We start comparing ![]() and
and ![]() . By Example 3.6,
. By Example 3.6, ![]() is reducible to
is reducible to ![]() . Concerning the converse we have the following.
. Concerning the converse we have the following.
Corollary 7.5. If ![]() is reducible to
is reducible to ![]() , then
, then
![]() $\mathsf {NE}\subseteq \mathsf {LINH}$
.
$\mathsf {NE}\subseteq \mathsf {LINH}$
.
Proof By Theorem 7.4(i), ![]() . If
. If ![]() is reducible to
is reducible to ![]() , then
, then ![]() by Lemma 7.2(ii). This implies
by Lemma 7.2(ii). This implies
![]() $\mathsf {NE}\subseteq \mathsf {LINH}$
by Theorem 7.4(ii).
$\mathsf {NE}\subseteq \mathsf {LINH}$
by Theorem 7.4(ii).
Adapting a mode of speech from [Reference Chen and Flum8], call an almost tally problem
![]() $(Q,\kappa )$
slicewise monotone if
$(Q,\kappa )$
slicewise monotone if
![]() $(1^n,x)\in Q$
implies
$(1^n,x)\in Q$
implies
![]() $(1^m,x)\in Q$
for all
$(1^m,x)\in Q$
for all
![]() $x\in \{0,1\}^*$
and all
$x\in \{0,1\}^*$
and all
![]() $n, m\in \mathbb {N}$
with
$n, m\in \mathbb {N}$
with
![]() $n<m$
. One can show that
$n<m$
. One can show that ![]() is the hardest such problem in
is the hardest such problem in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
. This is an easy modification of the proof of Lemma 3.12 and strengthens [Reference Chen and Flum8, Proposition 11]:
$\mathsf {para}\text {-}\mathsf {NP}$
. This is an easy modification of the proof of Lemma 3.12 and strengthens [Reference Chen and Flum8, Proposition 11]:
Corollary 7.6. Every almost tally problem in
![]() $\mathsf {para}\text {-}\mathsf {NP}$
that is slicewise monotone is reducible to
$\mathsf {para}\text {-}\mathsf {NP}$
that is slicewise monotone is reducible to ![]() .
.
We turn to ![]() and
and ![]() .
.
Corollary 7.7.
-
(i) If
 is reducible to
is reducible to  , then
, then
 $\mathsf {NE}\not \subseteq \mathsf {LINH}$
.
$\mathsf {NE}\not \subseteq \mathsf {LINH}$
. -
(ii) If
 is reducible to
is reducible to  , then
, then
 $\mathsf {NE}\subseteq \mathsf {LINH}$
.
$\mathsf {NE}\subseteq \mathsf {LINH}$
. -
(iii)
 and
and  are not equivalent.
are not equivalent.
Proof (iii) follows from (i) and (ii). For (i), assume ![]() is reducible to
is reducible to ![]() . Then
. Then ![]() and
and
![]() $\mathsf {NE}\not \subseteq \mathsf {LINH}$
follows by Theorem 1.3.
$\mathsf {NE}\not \subseteq \mathsf {LINH}$
follows by Theorem 1.3.
For (ii), assume ![]() is reducible to
is reducible to ![]() . Then
. Then ![]() by Proposition 7.3 and Lemma 7.2(i). This implies
by Proposition 7.3 and Lemma 7.2(i). This implies
![]() $\mathsf {NE}\subseteq \mathsf {LINH}$
by Remark 3.10.
$\mathsf {NE}\subseteq \mathsf {LINH}$
by Remark 3.10.
Finally, we turn to ![]() :
:
Proposition 7.8. Both ![]() and
and ![]() are reducible to
are reducible to ![]() .
.
Proof It is straightforward to compute from a nondeterministic Turing machine
![]() $\mathbb M$
a first-order sentence
$\mathbb M$
a first-order sentence
![]() $\varphi _{\mathbb M}$
that has a model of size n if and only if
$\varphi _{\mathbb M}$
that has a model of size n if and only if
![]() $\mathbb M$
accepts the empty input in exactly n steps.
$\mathbb M$
accepts the empty input in exactly n steps.
Concerning ![]() , by Lemma 4.1, it suffices to show that
, by Lemma 4.1, it suffices to show that ![]() is reducible to
is reducible to ![]() : map an instance
: map an instance
![]() $(1^n,\varphi )$
of
$(1^n,\varphi )$
of ![]() to
to
![]() $(1^n,\varphi \wedge \psi )$
where
$(1^n,\varphi \wedge \psi )$
where
![]() $\psi $
is an
$\psi $
is an
![]() $L^{\text {r}}_{\text {ar}}$
-sentence whose finite models are exactly those isomorphic to some standard finite
$L^{\text {r}}_{\text {ar}}$
-sentence whose finite models are exactly those isomorphic to some standard finite
![]() $L^{\text {r}}_{\text {ar}}$
-structure.
$L^{\text {r}}_{\text {ar}}$
-structure.
Observe ![]() can be solved in nondeterministic time
can be solved in nondeterministic time
![]() $n^{f(k)}$
for some computable
$n^{f(k)}$
for some computable
![]() $f:\mathbb {N}\to \mathbb {N}$
where
$f:\mathbb {N}\to \mathbb {N}$
where
![]() $k:=|\varphi |$
is the parameter. Can the parameter be moved out of the exponent? We find it worthwhile to explicitly point out the following direct corollary of the previous proposition and Theorem 1.3:
$k:=|\varphi |$
is the parameter. Can the parameter be moved out of the exponent? We find it worthwhile to explicitly point out the following direct corollary of the previous proposition and Theorem 1.3:
Corollary 7.9. If ![]() , then
, then
![]() $\mathsf {NE} \not \subseteq \mathsf {LINH}$
.
$\mathsf {NE} \not \subseteq \mathsf {LINH}$
.
Acknowledgements
We thank the anonymous referees for their detailed comments. A partial conference version of this article appeared as [Reference Chen, Müller and Yokoyama13].
Funding
Yijia Chen is supported by the National Natural Science Foundation of China (Project 62372291). Keita Yokoyama is partially supported by JSPS KAKENHI grant numbers JP19K03601, JP21KK0045, and JP23K03193.