No CrossRef data available.
Article contents
A DIMENSIONAL RESULT ON THE PRODUCT OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
Published online by Cambridge University Press: 11 October 2021
Abstract
This paper is concerned with the growth rate of the product of consecutive partial quotients relative to the denominator of the convergent for the continued fraction expansion of an irrational number. More precisely, given a natural number
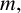 $m,$
we determine the Hausdorff dimension of the following set:
$m,$
we determine the Hausdorff dimension of the following set:
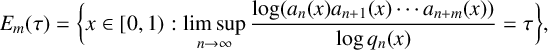 $$ \begin{align*} E_m(\tau)=\bigg\{x\in [0,1): \limsup\limits_{n\rightarrow\infty}\frac{\log (a_n(x)a_{n+1}(x)\cdots a_{n+m}(x))}{\log q_n(x)}=\tau\bigg\}, \end{align*} $$
$$ \begin{align*} E_m(\tau)=\bigg\{x\in [0,1): \limsup\limits_{n\rightarrow\infty}\frac{\log (a_n(x)a_{n+1}(x)\cdots a_{n+m}(x))}{\log q_n(x)}=\tau\bigg\}, \end{align*} $$
where
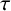 $\tau $
is a nonnegative number. This extends the dimensional result of Dirichlet nonimprovable sets (when
$\tau $
is a nonnegative number. This extends the dimensional result of Dirichlet nonimprovable sets (when
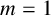 $m=1$
) shown by Hussain, Kleinbock, Wadleigh and Wang.
$m=1$
) shown by Hussain, Kleinbock, Wadleigh and Wang.
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 113 , Issue 3 , December 2022 , pp. 357 - 385
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Dzmitry Badziahin
This work was supported by NSFC (Grant Nos. 12001190 and 11871208) and the Science and Technology Development Fund, Macau SAR (no. 0024/2018/A1).



