Hostname: page-component-7479d7b7d-m9pkr Total loading time: 0 Render date: 2024-07-12T19:10:45.605Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of weighted Bergman-Orlicz spaces on the unit ball in Cn

Part of: Holomorphic functions of several complex variables

Published online by Cambridge University Press:  09 April 2009

Yasuo Matsugu  and
Jun Miyazawa
Jun Miyazawa
Affiliation:
Department of Mathematical Sciences Faculty of Science Shinshu University390–8621 MatsumotoJapan e-mail: matsugu@math.shinshu-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B denote the unit ball in Cn, and ν the normalized Lebesgue measure on B. For α > −1, define 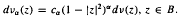Here cα is a positive constant such that να(B) = 1. Let H(B) denote the space of all holomorphic functions in B. For a twice differentiable, nondecreasing, nonnegative strongly convex function ϕ on the real line R, define the Bergman-Orlicz space Aϕ(να) by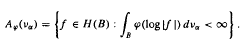

In this paper we prove that a function f ∈ H(B) is in Aϕ(να) if and only if 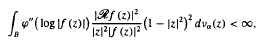where 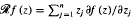is the radial derivative of f.

MSC classification

Secondary: 32A36: Bergman spaces 32A35: $H^p$-spaces, Nevanlinna spaces 32A37: Other spaces of holomorphic functions (e.g. bounded mean oscillation (BMOA), vanishing mean oscillation (VMOA))
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 74 , Issue 1 , February 2003 , pp. 5 - 18
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Beatrous, F. and Burbea, J., ‘Characterizations of spaces of holomorphic functions in the ball’, Kodai Math. J. 8 (1985), 36–51.CrossRefGoogle Scholar
[2]Ouyang, C. and Riihentaus, J., ‘A characterization of Hardy-Orlicz spaces on Cn’, Math. Scand. 80 (1997), 25–40.CrossRefGoogle Scholar
[3]Rudin, W., Function theory in the unit ball of Cn (Springer, Berlin, 1980).CrossRefGoogle Scholar
[4]Stoll, M., ‘Harmonic majorants for plurisubharmonic functions on bounded symmetric domains with applications to the spaces HΦ and N*’, J. Reine Angew. Math. 282 (1976), 80–87.Google Scholar
[5]Stoll, M., ‘A characterization of Hardy-Orlicz spaces on planar domains’, Proc. Amer. Math. Soc. 117 (1993), 1031–1038.CrossRefGoogle Scholar
[6]Stoll, M., ‘A characterization of Hardy spaces on the unit ball of Cn’, J. London Math. Soc. 48 (1993), 126–136.Google Scholar
[7]Stoll, M., Invariant potential theory in the unit ball of Cn (Cambridge Univ. Press, 1994).CrossRefGoogle Scholar
[8]Yamashita, S., ‘Criteria for functions to be of Hardy class H p’, Proc. Amer. Math. Soc. 75 (1979), 69–72.Google Scholar