Hostname: page-component-6d856f89d9-76ns8 Total loading time: 0 Render date: 2024-07-16T06:15:38.729Z Has data issue: false hasContentIssue false
  • English
  • Français

A formula for the resolvent of a Reynolds operator

Published online by Cambridge University Press:  09 April 2009

J. B. Miller
J. B. Miller
Affiliation:
Monash University Melbourne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 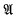be a complex Banach algebra, possibly non-commutative, with identity e. By a Reynolds operator we mean here a bounded linear operator T: 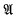→ 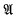satisfying the Reynolds identity 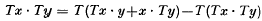for all x, y ∈ 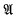. We prove that under certain conditions the resolvent of T, R(p, T) = (pI−T)−1, has the form 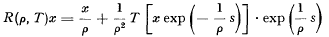where s = −log(e−Te) and exp y = e+y+y2/2!+….

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 3 , August 1968 , pp. 447 - 456
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Atkinson, F. V., ‘Some aspects of Baxter's functional equation’, J. of Math. Anal, and Applic. 7 (1963), 1–30.CrossRefGoogle Scholar
[2]Baxter, G., ‘An analytic problem whose solution follows from a simple algebraic identity’, Pac. J. of Math. 10 (1960), 731–742.CrossRefGoogle Scholar
[3]Gamlen, J. L. B. and Miller, J. B., ‘Averaging and Reynolds operators on Banach algebras, II. Spectral properties of averaging operators’, J. of Math. Anal, and Applic. (to appear).Google Scholar
[4]Hille, E., ‘On roots and logarithms of elements of a complex Banach algebra’, Math. Annalen 136 (1958), 46–57.CrossRefGoogle Scholar
[5]Miller, J. B., ‘Some properties of Baxter operators’, Acta Math. Acad. Sci. Hungar. 17 (1966), 387–400.CrossRefGoogle Scholar
[6]Miller, J. B., ‘Averaging and Reynolds operators on Banach algebras, I. Representation by derivations and antiderivations’, J. of Math. Anal, and Applic. 14 (1966), 527–548.CrossRefGoogle Scholar
[7]Miller, J. B., ‘Baxter operators and endomorphisms on Banach algebras’ (to appear).Google Scholar