Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-17T20:35:42.241Z Has data issue: false hasContentIssue false
  • English
  • Français

FUNCTORIAL ASPECTS OF THE RECONSTRUCTION OF LIE GROUPOIDS FROM THEIR BISECTIONS

Part of: Pseudogroups, differentiable groupoids and general structures on manifolds Categories and theories General theory of categories and functors Lie groups

Published online by Cambridge University Press:  14 March 2016

ALEXANDER SCHMEDING  and
CHRISTOPH WOCKEL
ALEXANDER SCHMEDING
Affiliation:
NTNU Trondheim, Alfred Getz’ vei 1, 7034 Trondheim, Norway email alexander.schmeding@math.ntnu.no
CHRISTOPH WOCKEL*
Affiliation:
Georg-August-Universität Göttingen, Bunsenstrasse 3–5, D-37073 Göttingen, Germany email christoph@wockel.eu
*
✉christoph@wockel.eu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

To a Lie groupoid over a compact base 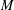$M$, the associated group of bisection is an (infinite-dimensional) Lie group. Moreover, under certain circumstances one can reconstruct the Lie groupoid from its Lie group of bisections. In the present article we consider functorial aspects of these construction principles. The first observation is that this procedure is functorial (for morphisms fixing 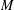$M$). Moreover, it gives rise to an adjunction between the category of Lie groupoids over 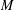$M$ and the category of Lie groups acting on 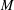$M$. In the last section we then show how to promote this adjunction to almost an equivalence of categories.

Keywords

Lie groupoidinfinite-dimensional Lie groupmapping spacebisection functoradjoint functorscomonad

MSC classification

Primary: 18A40: Adjoint functors (universal constructions, reflective subcategories, Kan extensions, etc.)
Secondary: 22E65: Infinite-dimensional Lie groups and their Lie algebras 58H05: Pseudogroups and differentiable groupoids 18C15: Triples (= standard construction, monad or triad), algebras for a triple, homology and derived functors for triples
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 101 , Issue 2 , October 2016 , pp. 253 - 276
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Adámek, J., Herrlich, H. and Strecker, G. E., ‘Abstract and concrete categories: the joy of cats’, Repr. Theory Appl. Categ. 17 (2006), 1–507, reprint of the 1990 original.Google Scholar
Barr, M. and Wells, C., ‘Toposes, triples and theories’, Repr. Theory Appl. Categ. 12 (2005), 1–288, corrected reprint of the 1985 original.Google Scholar
Bertram, W., Glöckner, H. and Neeb, K.-H., ‘Differential calculus over general base fields and rings’, Expo. Math. 22(3) (2004), 213–282.Google Scholar
Glöckner, H., ‘Infinite-dimensional Lie groups without completeness restrictions’, in: Geometry and Analysis on Finite- and Infinite-Dimensional Lie Groups (Bedlewo, 2000), Banach Center Publications, 55 (Polish Academy of Sciences, Warsaw, 2002), 43–59.Google Scholar
Glöckner, H., ‘Fundamentals of submersions and immersions between infinite-dimensional manifolds’, arXiv:1502.05795, 2015.Google Scholar
Glöckner, H., ‘Regularity properties of infinite-dimensional Lie groups, and semiregularity’,arXiv:1208.0715, 2015.Google Scholar
Heinloth, J., ‘Notes on differentiable stacks’, in: Mathematisches Institut, Georg-August-Universität Göttingen: Seminars Winter Term 2004/2005 (Universitätsdrucke Göttingen, Göttingen, 2005), 1–32.Google Scholar
Kriegl, A. and Michor, P. W., The Convenient Setting of Global Analysis, Mathematical Surveys and Monographs, 53 (American Mathematical Society, Providence, RI, 1997).Google Scholar
Mac Lane, S. and Moerdijk, I., Sheaves in Geometry and Logic, Universitext, A First Introduction to Topos Theory (Springer, New York, 1994), corrected reprint of the 1992 edition.CrossRefGoogle Scholar
Mackenzie, K. C. H., General Theory of Lie Groupoids and Lie Algebroids, London Mathematical Society Lecture Note Series, 213 (Cambridge University Press, Cambridge, 2005).Google Scholar
Michor, P. W., Manifolds of Differentiable Mappings, Shiva Mathematics Series, 3 (Shiva, Nantwich, 1980).Google Scholar
Neeb, K.-H., ‘Central extensions of infinite-dimensional Lie groups’, Ann. Inst. Fourier (Grenoble) 52(5) (2002), 1365–1442.Google Scholar
Neeb, K.-H., ‘Abelian extensions of infinite-dimensional Lie groups’, in: Travaux Mathématiques. Fasc., XV, Travaux Math., XV (University of Luxembourg, Luxembourg, 2004), 69–194.Google Scholar
Neeb, K.-H., ‘Towards a Lie theory of locally convex groups’, Jpn. J. Math. 1(2) (2006), 291–468.Google Scholar
Neeb, K.-H., ‘Non-abelian extensions of infinite-dimensional Lie groups’, Ann. Inst. Fourier (Grenoble) 57(1) (2007), 209–271.CrossRefGoogle Scholar
Neeb, K.-H. and Salmasian, H., ‘Differentiable vectors and unitary representations of Fréchet–Lie supergroups’, Math. Z. 275(1–2) (2013), 419–451.CrossRefGoogle Scholar
Rybicki, T., ‘A Lie group structure on strict groups’, Publ. Math. Debrecen 61(3–4) (2002), 533–548.Google Scholar
Schmeding, A. and Wockel, C., ‘The Lie group of bisections of a Lie groupoid’, Ann. Global Anal. Geom. 48(1) (2015), 87–123.Google Scholar
Schmeding, A. and Wockel, C., ‘(Re)constructing Lie groupoids from their bisections and applications to prequantisation’, arXiv:1506.05415, 2015.Google Scholar
Wockel, C., Infinite-dimensional and Higher Structures in Differential Geometry, Lecture Notes for a Course given at the University of Hamburg (2013), http://www.math.uni-hamburg.de/home/wockel/teaching/higher_structures.html.Google Scholar