Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-20T08:06:28.164Z Has data issue: false hasContentIssue false
  • English
  • Français

THE PRO-$\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  22 December 2023

CLAUDE MARION ,
PEDRO V. SILVA  and
GARETH TRACEY
CLAUDE MARION
Affiliation:
Centro de Matemática, Faculdade de Ciências, Universidade do Porto, R. Campo Alegre 687, 4169-007 Porto, Portugal e-mail: claude.marion@fc.up.pt
PEDRO V. SILVA
Affiliation:
Centro de Matemática, Faculdade de Ciências, Universidade do Porto, R. Campo Alegre 687, 4169-007 Porto, Portugal e-mail: pvsilva@fc.up.pt
GARETH TRACEY*
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK
*
e-mail: Gareth.Tracey@warwick.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that, given a finitely generated subgroup H of a free group F, the following questions are decidable: is H closed (dense) in F for the pro-(met)abelian topology? Is the closure of H in F for the pro-(met)abelian topology finitely generated? We show also that if the latter question has a positive answer, then we can effectively construct a basis for the closure, and the closure has decidable membership problem in any case. Moreover, it is decidable whether H is closed for the pro-$\mathbf {V}$ topology when 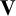$\mathbf {V}$ is an equational pseudovariety of finite groups, such as the pseudovariety $\mathbf {S}_k$ of all finite solvable groups with derived length 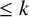$\leq k$. We also connect the pro-abelian topology with the topologies defined by abelian groups of bounded exponent.

Keywords

subgroups of the free groupequational pseudovarietypro-k-solvable topologypro-abelian topologypro-metabelian topology

MSC classification

Primary: 20E05: Free nonabelian groups 20E10: Quasivarieties and varieties of groups 20F10: Word problems, other decision problems, connections with logic and automata 20F22: Other classes of groups defined by subgroup chains
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 116 , Issue 3 , June 2024 , pp. 363 - 383
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Ben Martin

The first author acknowledges support from the Centre of Mathematics of the University of Porto, which is financed by national funds through the Fundação para a Ciência e a Tecnologia, I.P., under the project with references UIDB/00144/2020 and UIDP/00144/2020. The second author acknowledges support from the Centre of Mathematics of the University of Porto, which is financed by national funds through the Fundação para a Ciência e a Tecnologia, I.P., under the project with reference UIDB/00144/2020. The third author was supported by the Engineering and Physical Sciences Research Council, grant number EP/T017619/1.

References

Agalakov, S. A., ‘Finite separability of groups and Lie algebras’, Algebra Logika 22(4) (1985), 363–371.Google Scholar
Alibabaei, K., ‘On the profinite topology on solvable groups’, J. Group Theory 20(4) (2017), 729–743.CrossRefGoogle Scholar
Alperin, R. C., ‘Metabelian wreath products are LERF’, Preprint, 2006, arXiv:0609611.Google Scholar
Auinger, K. and Steinberg, B., ‘Varieties of finite supersolvable groups with the M. Hall property’, Math. Ann. 335 (2006), 853–877.10.1007/s00208-006-0767-2CrossRefGoogle Scholar
Bartholdi, L. and Siva, P. V., ‘Rational subsets of groups’, in: Handbook of Automata Theory (ed. Pin, J.-E.) (EMS Press, Berlin, 2021) Ch. 23.Google Scholar
Coulbois, T., ‘Propriétés de Ribes-Zalesskiǐ, topologie profinie produit libre et généralisations’, PhD Thesis, Université Paris 7, 2000.Google Scholar
Delgado, M., ‘Abelian pointlikes of a monoid’, Semigroup Forum 56 (1998), 339–361.CrossRefGoogle Scholar
Gruenberg, K. W., ‘Residual properties of infinite soluble groups’, Proc. Lond. Math. Soc. (3) 7 (1957), 29–62.CrossRefGoogle Scholar
Hall, M. Jr, ‘Coset representations in free groups’, Trans. Amer. Math. Soc. 67 (1949), 421–432.CrossRefGoogle Scholar
Hall, M. Jr, ‘A topology for free groups and related groups’, Ann. of Math. (2) 52 (1950), 127–139.CrossRefGoogle Scholar
Hall, P., ‘On the finiteness of certain soluble groups’, Proc. Lond. Math. Soc. (3) 9 (1959), 595–622.CrossRefGoogle Scholar
Hungerford, T., Algebra, Graduate Texts in Mathematics, 73 (Springer-Verlag, New York–Berlin, 1980).CrossRefGoogle Scholar
Karrass, A. and Solitar, D., ‘Note on a theorem of Schreier’, Proc. Amer. Math. Soc. 8 (1957), 696–697.CrossRefGoogle Scholar
Margolis, S., Sapir, M. and Weil, P., ‘Closed subgroups in pro- $\mathbf{V}$ topologies and the extension problem for inverse automata’, Internat. J. Algebra Comput. 11 (2001), 405–445.CrossRefGoogle Scholar
Marion, C., Silva, P. V. and Tracey, G., ‘On the pseudovariety of groups $\mathbf{U}={\vee}_{p\in \mathbb{P}}\ \mathbf{Ab}(p)\ast \mathbf{Ab}(p-1)$ ’, Preprint, 2023, arXiv:2304.10522.Google Scholar
Marion, C., Silva, P. V. and Tracey, G., ‘On the closure of cyclic subgroups of a free group in pro- $\mathbf{V}$ topologies’, Preprint, 2023, arXiv:2304.10230.Google Scholar
Marion, C., Silva, P. V. and Tracey, G., ‘The pro-supersolvable topology on a free group: deciding denseness’, Preprint, 2023, arXiv:2304.10501.CrossRefGoogle Scholar
Neumann, H., Varieties of Groups (Springer-Verlag, Berlin–Heidelberg, 1967).CrossRefGoogle Scholar
Rhodes, J. and Steinberg, B., The q-Theory of Finite Semigroups, Springer Monographs in Mathematics (Springer, New York, 2009).CrossRefGoogle Scholar
Ribes, L. and Zalesskiǐ, P. A., ‘The pro- $p$ topology of a free group and algorithmic problems in semigroups’, Internat. J. Algebra Comput. 4(3) (1994), 359–374.CrossRefGoogle Scholar
Romanovskiǐ, N. S., ‘The occurrence problem for extensions of abelian groups by nilpotent groups’, Sibirsk. Mat. Zh. 21 (1980), 170–174.Google Scholar
Stallings, J. R., ‘Topology of finite graphs’, Invent. Math. 71 (1983), 551–565.CrossRefGoogle Scholar
Steinberg, B., ‘Monoid kernels and profinite topologies on the free Abelian group’, Bull. Aust. Math. Soc. 60(3) (1999), 391–402.CrossRefGoogle Scholar
Umirbaev, U. U., ‘The occurrence problem for free solvable groups’, SibirskiǐFond Algebry Logiki Algebra Logika 34(2) (1995), 211–232, 243.Google Scholar