Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-07T08:35:33.571Z Has data issue: false hasContentIssue false
  • English
  • Français

ROUGH INTEGERS WITH A DIVISOR IN A GIVEN INTERVAL

Part of: Nonparametric inference Multiplicative number theory

Published online by Cambridge University Press:  08 January 2020

KEVIN FORD
KEVIN FORD*
Affiliation:
Department of Mathematics, 1409 West Green Street, University of Illinois at Urbana-Champaign, Urbana, IL61801, USA e-mail: ford126@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine, up to multiplicative constants, the number of integers 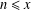$n\leq x$ that have a divisor in 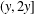$(y,2y]$ and no prime factor 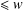$\leq w$. Our estimate is uniform in 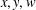$x,y,w$. We apply this to determine the order of the number of distinct integers in the 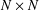$N\times N$ multiplication table, which are free of prime factors 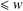$\leq w$, and the number of distinct fractions of the form 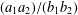$(a_{1}a_{2})/(b_{1}b_{2})$ with 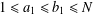$1\leq a_{1}\leq b_{1}\leq N$ and 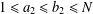$1\leq a_{2}\leq b_{2}\leq N$.

Keywords

divisorsFarey fractions

MSC classification

Primary: 11N25: Distribution of integers with specified multiplicative constraints
Secondary: 62G30: Order statistics; empirical distribution functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 1 , August 2021 , pp. 17 - 36
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by I. Shparlinski

Research supported by National Science Foundation grant DMS-1802139.

References

Erdős, P., ‘On the greatest prime factor of ∏ k=1 x f (k)’, J. Lond. Math. Soc. (2) 27 (1952), 379–384.Google Scholar
Erdős, P., ‘Some remarks on number theory’, Riveon Lematematika 9 (1955), 45–48 (Hebrew. English summary).Google Scholar
Erdős, P., ‘An asymptotic inequality in the theory of numbers’, Vestnik Leningrad. Univ. (13) 15 (1960), 41–49 (in Russian).Google Scholar
Erdős, P. and Schinzel, A., ‘On the greatest prime factor of ∏ k=1 x f (k)’, Acta Arith. (2) 55 (1990), 191–200.Google Scholar
Ford, K., ‘The distribution of integers with a divisor in a given interval’, Ann. Math. 168 (2008), 367–433.Google Scholar
Ford, K., ‘Integers with a divisor in (y, 2y]’, in: Anatomy of Integers, CRM Proceedings and Lecture Notes, 46 (eds. De Koninck, J.-M., Granville, A. and Luca, F.) (Providence, RI, 2008), 65–80.Google Scholar
Ford, K., Khan, M. R., Shparlinski, I. E. and Yankov, C. L., ‘On the maximal difference between an element and its inverse in residue rings’, Proc. Amer. Math. Soc. (12) 133 (2005), 3463–3468.Google Scholar
Halberstam, H. and Richert, H.-E., Sieve Methods, London Mathematical Society Monographs, 4 (Academic Press, 1974).Google Scholar
Koukoulopoulos, D., ‘Divisors of shifted primes’, Int. Math. Res. Not. IMRN (24) 2010 (2010), 4585–4627.Google Scholar
Koukoulopoulos, D., ‘Localized factorizations of integers’, Proc. Lond. Math. Soc. 101 (2010), 392–426.Google Scholar
Norton, K. K., ‘On the number of restricted prime factors of an integer. I’, Illinois J. Math. (4) 20 (1976), 681–705.Google Scholar
Tenenbaum, G., ‘Sur une question d’Erdős et Schinzel’, in: A Tribute to Paul Erdős (Cambridge University Press, Cambridge, 1990), 405–443.Google Scholar
Tenenbaum, G., ‘Sur une question d’Erdős et Schinzel. II’, Invent. Math. (1) 99 (1990), 215–224.Google Scholar