Hostname: page-component-84b7d79bbc-dwq4g Total loading time: 0 Render date: 2024-07-28T17:23:43.513Z Has data issue: false hasContentIssue false
  • English
  • Français

EULER CHARACTERISTIC AND SIGNATURE OF REAL SEMI-STABLE DEGENERATIONS

Published online by Cambridge University Press:  21 February 2022

Erwan Brugallé Open the ORCID record for Erwan Brugallé [Opens in a new window]
Erwan Brugallé*
Affiliation:
Université de Nantes, Laboratoire de Mathématiques Jean Leray, 2 rue de la Houssinière, F-44322 Nantes, Cedex 3, France
*
erwan.brugalle@math.cnrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a motivic proof of the fact that for nonsingular real tropical complete intersections, the Euler characteristic of the real part is equal to the signature of the complex part. This was originally proved by Itenberg in the case of surfaces in 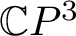$\mathbb {C}P^{3}$, and has been successively generalized by Bertrand and by Bihan and Bertrand. Our proof, different from previous approaches, is an application of the motivic nearby fiber of semistable degenerations. In particular, it extends the original result by Itenberg, Bertrand, and Bihan to real analytic families admitting a 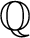$\mathbb {Q}$-nonsingular tropical limit.

Keywords

topology of real algebraic varietiessemistable degenerationscombinatorial patchworkingtropical geometry

MSC classification

Primary: 14P25: Topology of real algebraic varieties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 5 , September 2023 , pp. 2447 - 2454
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnal, C., Patchwork combinatoire et topologie d’hypersurfaces algébriques réelles , Master’s thesis, Institut de Mathématiques de Jussieu, Paris Rive Gauche Sorbonne Université, 2017.Google Scholar
Bertrand, B., Euler characteristic of primitive $T$ -hypersurfaces and maximal surfaces, J. Inst. Math. Jussieu 9(1) (2010), 1–27.CrossRefGoogle Scholar
Bertrand, B. and Bihan, F., ‘Euler characteristic of real nondegenerate tropical complete intersections’, Preprint, 2007, https://arxiv.org/abs/0710.1222.Google Scholar
Bittner, F., On motivic zeta functions and the motivic nearby fiber, Math. Z. 249(1) (2005), 63–83.CrossRefGoogle Scholar
Brugallé, E., Itenberg, I., Mikhalkin, G. and Shaw, K., Brief introduction to tropical geometry, in Proceedings of the Gökova Geometry-Topology Conference 2014, pp. 1–75 (Gökova Geometry/Topology Conference (GGT), Gökova, Turkey, 2015).Google Scholar
Degtyarev, A. I. and Kharlamov, V. M., Topological properties of real algebraic varieties: Rokhlin’s way, Russian Math. Surveys 55(4) (2000), 735–814.CrossRefGoogle Scholar
Denef, J. and Loeser, F., Geometry on arc spaces of algebraic varieties, in European Congress of Mathematics, Vol. I (Barcelona, 2000), Progress in Mathematics, 201, pp. 327–348 (Birkhäuser, Basel, 2001).Google Scholar
Fulton, W., Introduction to Toric Varieties, Annals of Mathematics Studies, 131 (Princeton University Press, Princeton, NJ, 1993).CrossRefGoogle Scholar
Helm, D. and Katz, E., Monodromy filtrations and the topology of tropical varieties, Canad. J. Math. 64(4) (2012), 845–868.CrossRefGoogle Scholar
Itenberg, I., Topology of real algebraic $T$ -surfaces, Real algebraic and analytic geometry (Segovia, 1995), Rev. Mat. Univ. Complut. Madrid. 10 (1997), 131–152.Google Scholar
Itenberg, I., Katzarkov, L., Mikhalkin, G. and Zharkov, I., Tropical homology, Math. Ann. 374(1-2) (2019), 963–1006.CrossRefGoogle Scholar
Itenberg, I. and Shustin, E., Viro theorem and topology of real and complex combinatorial hypersurfaces, Israel J. Math. 133 (2003), 189–238.CrossRefGoogle Scholar
Katz, E. and Stapledon, A., Tropical geometry and the motivic nearby fiber, Compos. Math. 148(1) (2012), 269–294.CrossRefGoogle Scholar
Katz, E. and Stapledon, A., Tropical geometry, the motivic nearby fiber, and limit mixed Hodge numbers of hypersurfaces, Res. Math. Sci., 3 (2016), Paper No. 10, 36.CrossRefGoogle Scholar
Mangolte, F., Variétés algébriques réelles, Cours Spécialisés, 24 (Société Mathématique de France, Paris, 2017).Google Scholar
Mikhalkin, G. and Rau, J., ‘Tropical geometry’, Preliminary version, https://math.uniandes.edu.co/~j.rau/downloads/main.pdf.Google Scholar
Peters, C., Motivic Aspects of Hodge Theory, Vol. 92 (Narosa Publishing House, New Delhi, 2010).Google Scholar
Peters, C. and Steenbrink, J., Mixed Hodge Structures, Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge, 52 (Springer-Verlag, Berlin, 2008).Google Scholar
Rau, J., Renaudineau, A. and Shaw, K., ‘Real phase structure on tropical varieties’, In preparation, 2022.Google Scholar
Renaudineau, A. and Shaw, K., ‘Bounding the Betti numbers of real hypersurfaces near the tropical limit, Preprint, 2018, https://arxiv.org/abs/1805.02030.Google Scholar
Voisin, C., Théorie de Hodge et géométrie algébrique complexe, Cours Spécialisés, 10 (Société Mathématique de France, Paris, 2002).Google Scholar