Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-06-03T01:16:51.006Z Has data issue: false hasContentIssue false
  • English
  • Français

LINEAR INDEPENDENCE IN THE RATIONAL HOMOLOGY COBORDISM GROUP

Part of: Low-dimensional topology

Published online by Cambridge University Press:  28 August 2019

Marco Golla Open the ORCID record for Marco Golla [Opens in a new window]  and
Kyle Larson
Marco Golla
Affiliation:
CNRS, Laboratoire de Mathématiques Jean Leray, Nantes, France (marco.golla@univ-nantes.fr)
Kyle Larson
Affiliation:
Alfréd Rényi Institute of Mathematics, Budapest, Hungary (larson@renyi.mta.hu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We give simple homological conditions for a rational homology 3-sphere $Y$ to have infinite order in the rational homology cobordism group 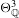$\unicode[STIX]{x1D6E9}_{\mathbb{Q}}^{3}$, and for a collection of rational homology spheres to be linearly independent. These translate immediately to statements about knot concordance when $Y$ is the branched double cover of a knot, recovering some results of Livingston and Naik. The statements depend only on the homology groups of the 3-manifolds, but are proven through an analysis of correction terms and their behavior under connected sums.

Keywords

homology cobordismknot concordancecorrection terms

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds
Secondary: 57M25: Knots and links in $S^3$
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 3 , May 2021 , pp. 989 - 1000
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aceto, P. and Larson, K., Knot concordance and homology sphere groups, Int. Math. Res. Not. IMRN 2018(23) (2018), 7318–7334.CrossRefGoogle Scholar
Casson, A. J. and Harer, J. L., Some homology lens spaces which bound rational homology balls, Pacific J. Math. 96(1) (1981), 23–36.CrossRefGoogle Scholar
Frøyshov, K. A., The Seiberg–Witten equations and four-manifolds with boundary, Math. Res. Lett. 3(3) (1996), 373–390.CrossRefGoogle Scholar
Hedden, M., Livingston, C. and Ruberman, D., Topologically slice knots with nontrivial Alexander polynomial, Adv. Math. 231(2) (2012), 913–939.CrossRefGoogle Scholar
Kaplan, S. J., Constructing framed 4-manifolds with given almost framed boundaries, Trans. Amer. Math. Soc. 254 (1979), 237–263.Google Scholar
Kim, S.-G. and Livingston, C., Nonsplittability of the rational homology cobordism group of 3-manifolds, Pacific J. Math. 271(1) (2014), 183–211.CrossRefGoogle Scholar
Kirby, R. (Ed.) Problems in low-dimensional topology, in Geometric Topology (Athens, GA, 1993), AMS/IP Stud. Adv. Math., Volume 2, pp. 35–473 (American Mathematical Society, Providence, RI, 1997).Google Scholar
Lisca, P., Sums of lens spaces bounding rational balls, Algebr. Geom. Topol. 7 (2007), 2141–2164.CrossRefGoogle Scholar
Livingston, C. and Naik, S., Obstructing four-torsion in the classical knot concordance group, J. Differential Geom. 51(1) (1999), 1–12.Google Scholar
Livingston, C. and Naik, S., Knot concordance and torsion, Asian J. Math. 5(1) (2001), 161–167.CrossRefGoogle Scholar
Owens, B. and Strle, S., Definite manifolds bounded by rational homology three spheres, in Geometry and Topology of Manifolds, Fields Inst. Commun., Volume 47, pp. 243–252 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Ozsváth, P. and Szabó, Z., Absolutely graded Floer homologies and intersection forms for four-manifolds with boundary, Adv. Math. 173(2) (2003), 179–261.CrossRefGoogle Scholar
Stipsicz, A. I., On the 𝜇 -invariant of rational surface singularities, Proc. Amer. Math. Soc. 136(11) (2008), 3815–3823.CrossRefGoogle Scholar
Wall, C. T. C., Quadratic forms on finite groups, and related topics, Topology 2 (1963), 281–298.CrossRefGoogle Scholar