Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T18:02:29.262Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 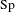$\text{Sp}$-DISTINGUISHED REPRESENTATIONS OF THE QUASI-SPLIT UNITARY GROUPS

Part of: Lie groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  17 April 2019

A. Mitra  and
Omer Offen
A. Mitra
Affiliation:
Indian Institute of Science Education and Research, Tirupati, India (00.arnab.mitra@gmail.com)
Omer Offen
Affiliation:
Brandeis University, Waltham, MA, USA (offen@brandeis.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study 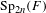$\text{Sp}_{2n}(F)$-distinction for representations of the quasi-split unitary group 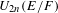$U_{2n}(E/F)$ in $2n$ variables with respect to a quadratic extension 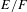$E/F$ of 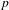$p$-adic fields. A conjecture of Dijols and Prasad predicts that no tempered representation is distinguished. We verify this for a large family of representations in terms of the Mœglin–Tadić classification of the discrete series. We further study distinction for some families of non-tempered representations. In particular, we exhibit $L$-packets with no distinguished members that transfer under base change to 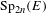$\text{Sp}_{2n}(E)$-distinguished representations of 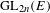$\text{GL}_{2n}(E)$.

Keywords

representations of p-adic reductive groupsdistinguished representationsquadratic base change

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 225 - 276
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anandavardhanan, U. K., Kable, A. C. and Tandon, R., Distinguished representations and poles of twisted tensor L-functions, Proc. Amer. Math. Soc. 132(10) (2004), 2875–2883, MR 2063106.CrossRefGoogle Scholar
Anandavardhanan, U. K. and Rajan, C. S., Distinguished representations, base change, and reducibility for unitary groups, Int. Math. Res. Not. IMRN (14) (2005), 841–854, MR 2146859.CrossRefGoogle Scholar
Bernšteĭn, I. N. and Zelevinskiĭ, A. V., Representations of the group GL(n, F), where F is a local non-Archimedean field, Uspekhi Mat. Nauk 31(3(189)) (1976), 5–70, MR 0425030 (54 #12988).Google Scholar
Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive p-adic groups. I, Ann. Sci. Éc. Norm. Supér. (4) 10(4) (1977), 441–472, MR 0579172 (58 #28310).CrossRefGoogle Scholar
Bernstein, J. N., On the support of Plancherel measure, J. Geom. Phys. 5(4) (1988), 663–710 (1989), MR 1075727 (91k:22027).CrossRefGoogle Scholar
Dijols, S. and Prasad, D., Symplectic models for unitary groups, Trans. Amer. Math. Soc., doi:10.1090/tran/7651.Google Scholar
Flicker, Y. Z., On distinguished representations, J. Reine Angew. Math. 418 (1991), 139–172, MR 1111204.Google Scholar
Flicker, Y. Z., Distinguished representations and a Fourier summation formula, Bull. Soc. Math. France 120(4) (1992), 413–465, MR 1194271.CrossRefGoogle Scholar
Flicker, Y. Z., On zeroes of the twisted tensor L-function, Math. Ann. 297(2) (1993), 199–219, MR 1241802.CrossRefGoogle Scholar
Gan, W. T., Gross, B. H. and Prasad, D., Symplectic local root numbers, central critical L values, and restriction problems in the representation theory of classical groups, Astérisque (346) (2012), 1–109. Sur les conjectures de Gross et Prasad. I. MR 3202556.Google Scholar
Gel’fand, I. M. and Kajdan, D. A., Representations of the group GL(n, K) where K is a local field, in Lie Groups and their Representations (Proc. Summer School, Bolyai János Math. Soc., Budapest, 1971), pp. 95–118 (Halsted, New York, 1975), MR 0404534 (53 #8334).Google Scholar
Goldberg, D., Some results on reducibility for unitary groups and local Asai L-functions, J. Reine Angew. Math. 448 (1994), 65–95, MR 1266747.Google Scholar
Gurevich, M., Ma, J.-J. and Mitra, A., On two questions concerning representations distinguished by the Galois involution, Forum Math. 30(1) (2018), 141–157, MR 3739332.CrossRefGoogle Scholar
Hanzer, M., The generalized injectivity conjecture for classical p-adic groups, Int. Math. Res. Not. IMRN (2) (2010), 195–237, MR 2581039 (2011b:22025).CrossRefGoogle Scholar
Harris, M. and Taylor, R., The Geometry and Cohomology of Some Simple Shimura Varieties, Annals of Mathematics Studies, 151, (Princeton University Press, Princeton, NJ, 2001). With an appendix by Vladimir G. Berkovich, MR MR1876802 (2002m:11050).Google Scholar
Heumos, M. J. and Rallis, S., Symplectic-Whittaker models for Gln , Pacific J. Math. 146(2) (1990), 247–279, MR 1078382 (91k:22036).CrossRefGoogle Scholar
Kret, A. and Lapid, E., Jacquet modules of ladder representations, C. R. Math. Acad. Sci. Paris 350(21–22) (2012), 937–940, MR 2996769.CrossRefGoogle Scholar
Kumanduri, R., Distinguished representations for unitary groups, Pacific J. Math. 178(2) (1997), 293–306, MR 1447416.CrossRefGoogle Scholar
Lapid, E. and Mínguez, A., On a determinantal formula of Tadić, Amer. J. Math. 136(1) (2014), 111–142, MR 3163355.CrossRefGoogle Scholar
Lapid, E. and Mínguez, A., On parabolic induction on inner forms of the general linear group over a non-archimedean local field, Selecta Math. (N.S.) 22(4) (2016), 2347–2400, MR 3573961.CrossRefGoogle Scholar
Lapid, E. and Tadić, M., Some results on reducibility of parabolic induction for classical groups, Amer. J. Math. (2017) (to appear) arXiv:1703.09475.Google Scholar
Lapid, E. M. and Rogawski, J. D., Periods of Eisenstein series: the Galois case, Duke Math. J. 120(1) (2003), 153–226, MR 2010737.Google Scholar
Matringe, N., Distinction of some induced representations, Math. Res. Lett. 17(1) (2010), 77–97, MR 2592729 (2011a:22021).CrossRefGoogle Scholar
Matringe, N., Distinguished generic representations of GL(n) over p-adic fields, Int. Math. Res. Not. IMRN (1) (2011), 74–95, MR 2755483 (2012f:22032).CrossRefGoogle Scholar
Mitra, A. and Offen, O., Vanishing of local symplectic periods for cuspidal representations of the unitary group, C. R. Math. Acad. Sci. Paris 355(1) (2017), 15–19, MR 3590280.CrossRefGoogle Scholar
Mitra, A., Offen, O. and Sayag, E., Klyachko models for ladder representations, Doc. Math. 22 (2017), 611–657, MR 3628792.Google Scholar
Mœglin, C., Classification et changement de base pour les séries discrètes des groupes unitaires p-adiques, Pacific J. Math. 233(1) (2007), 159–204, MR 2366373.CrossRefGoogle Scholar
Mœglin, C. and Tadić, M., Construction of discrete series for classical p-adic groups, J. Amer. Math. Soc. 15(3) (2002), 715–786 (electronic), MR 1896238 (2003g:22020).CrossRefGoogle Scholar
Mœglin, C., Vignéras, M.-F. and Waldspurger, J.-L., Correspondances de Howe Sur un Corps p-Adique, Lecture Notes in Mathematics, 1291, (Springer, Berlin, 1987), MR 1041060 (91f:11040).CrossRefGoogle Scholar
Mœglin, C. and Waldspurger, J.-L., Sur l’involution de Zelevinski, J. Reine Angew. Math. 372 (1986), 136–177, MR 863522 (88c:22019).Google Scholar
Mœglin, C. and Waldspurger, J.-L., Spectral Decomposition and Eisenstein Series, Cambridge Tracts in Mathematics, 113, (Cambridge University Press, Cambridge, 1995). Une paraphrase de l’Écriture [A paraphrase of Scripture], MR 1361168 (97d:11083).CrossRefGoogle Scholar
Mok, C. P., Endoscopic classification of representations of quasi-split unitary groups, Mem. Amer. Math. Soc. 235(1108) (2015), vi + 248, MR 3338302.Google Scholar
Morimoto, K., Model transitions for representations of unitary type, Int. Math. Res. Not. IMRN (to appear) doi:10.1093/imrn/rny048.CrossRefGoogle Scholar
Offen, O., On parabolic induction associated with a p-adic symmetric space, J. Number Theory 170 (2017), 211–227, MR 3541705.CrossRefGoogle Scholar
Offen, O. and Sayag, E., Uniqueness and disjointness of Klyachko models, J. Funct. Anal. 254(11) (2008), 2846–2865, MR 2414223.CrossRefGoogle Scholar
Sakellaridis, Y. and Venkatesh, A., Periods and harmonic analysis on spherical varieties, Astérisque (396) (2017), viii + 360, MR 3764130.Google Scholar
Silberger, A. J., The Langlands quotient theorem for p-adic groups, Math. Ann. 236(2) (1978), 95–104, MR 0507262 (58 #22413).CrossRefGoogle Scholar
Springer, T. A., Some results on algebraic groups with involutions, in Algebraic Groups and Related Topics (Kyoto/Nagoya, 1983), Adv. Stud. Pure Math., 6, pp. 525–543 (North-Holland, Amsterdam, 1985), MR 803346 (86m:20050).CrossRefGoogle Scholar
Tadić, M., Classification of unitary representations in irreducible representations of general linear group (non-Archimedean case), Ann. Sci. Éc. Norm. Supér. (4) 19(3) (1986), 335–382, MR 870688 (88b:22021).CrossRefGoogle Scholar
Tadić, M., Representations of p-adic symplectic groups, Compos. Math. 90(2) (1994), 123–181, MR 1266251 (95a:22025).Google Scholar
Tadić, M., On tempered and square integrable representations of classical p-adic groups, Sci. China Math. 56(11) (2013), 2273–2313, MR 3123571.CrossRefGoogle Scholar
Waldspurger, J.-L., La formule de Plancherel pour les groupes p-adiques (d’après Harish-Chandra), J. Inst. Math. Jussieu 2(2) (2003), 235–333, MR 1989693 (2004d:22009).CrossRefGoogle Scholar
Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n), Ann. Sci. Éc. Norm. Supér. (4) 13(2) (1980), 165–210, MR 584084 (83g:22012).CrossRefGoogle Scholar