Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-19T02:31:04.381Z Has data issue: false hasContentIssue false
  • English
  • Français

PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY

Part of: Topological $K$-theory (Co)homology theory Special varieties Homology and cohomology theories Algebraic combinatorics

Published online by Cambridge University Press:  11 February 2019

Cristian Lenart ,
Kirill Zainoulline Open the ORCID record for Kirill Zainoulline [Opens in a new window]  and
Changlong Zhong
Cristian Lenart
Affiliation:
Department of Mathematics and Statistics, State University of New York at Albany, Albany, NY12222, USA (clenart@albany.edu; czhong@albany.edu) URL: http://www.albany.edu/∼lenart/; http://www.albany.edu/∼cz954339/
Kirill Zainoulline
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, 150 Louis-Pasteur, Ottawa, ON, K1N 6N5, Canada (kirill@uottawa.ca) URL: http://mysite.science.uottawa.ca/kzaynull/
Changlong Zhong
Affiliation:
Department of Mathematics and Statistics, State University of New York at Albany, Albany, NY12222, USA (clenart@albany.edu; czhong@albany.edu) URL: http://www.albany.edu/∼lenart/; http://www.albany.edu/∼cz954339/
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the equivariant oriented cohomology ring 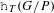$\mathtt{h}_{T}(G/P)$ of partial flag varieties using the moment map approach. We define the right Hecke action on this cohomology ring, and then prove that the respective Bott–Samelson classes in 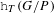$\mathtt{h}_{T}(G/P)$ can be obtained by applying this action to the fundamental class of the identity point, hence generalizing previously known results of Chow groups by Brion, Knutson, Peterson, Tymoczko and others. Our main result concerns the equivariant oriented cohomology theory $\mathfrak{h}$ corresponding to the 2-parameter Todd genus. We give a new interpretation of Deodhar’s parabolic Kazhdan–Lusztig basis, i.e., we realize it as some cohomology classes (the parabolic Kazhdan–Lusztig (KL) Schubert classes) in 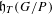$\mathfrak{h}_{T}(G/P)$. We make a positivity conjecture, and a conjecture about the relationship of such classes with smoothness of Schubert varieties. We also prove the latter in several special cases.

Keywords

Schubert calculuselliptic cohomologyflag varietyHecke algebraparabolic Kazhdan–Lusztig basis

MSC classification

Primary: 14M15: Grassmannians, Schubert varieties, flag manifolds 14F43: Other algebro-geometric (co)homologies (e.g., intersection, equivariant, Lawson, Deligne (co)homologies)
Secondary: 55N20: Generalized (extraordinary) homology and cohomology theories 55N22: Bordism and cobordism theories, formal group laws 19L47: Equivariant $K$-theory 05E99: None of the above, but in this section
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 6 , November 2020 , pp. 1889 - 1929
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arabia, A., Cycles de Schubert et cohomologie équivariante de K/T, Invent. Math. 85 (1986), 39–52.Google Scholar
Arabia, A., Cohomologie T-équivariante de la variété de drapeaux d’un groupe de Kac-Moody, Bull. Soc. Math. France 117 (1989), 129–165.Google Scholar
Bernstein, I. N., Gelfand, I. M. and Gelfand, S. I., Schubert cells and cohomology of the spaces G/P, Russian Math. Surveys 28 (1973), 1–26.Google Scholar
Björner, A. and Brenti, F., Combinatorics of Coxeter Groups, in Graduate Texts in Mathematics, Volume 231, ix+363 pp (Springer, 2005).Google Scholar
Bressler, P. and Evens, S., Schubert calculus in complex cobordisms, Trans. Amer. Math. Soc. 331(no.2) (1992), 799–813.Google Scholar
Bressler, P. and Evens, S., The Schubert calculus, braid relations and generalized cohomology, Trans. Amer. Math. Soc. 317 (1990), 799–811.Google Scholar
Brion, M., Equivariant Chow groups for torus actions, Transform. Groups 2 (1997), 225–267.Google Scholar
Buchstaber, V. and Kholodov, A., Formal groups, functional equations and generalized cohomology theories, Mat. Sb. 181 (1990), 75–94.Google Scholar
Calmès, B., Petrov, V. and Zainoulline, K., Invariants, torsion indices and cohomology of complete flags, Ann. Sci. Éc. Norm. Supér. (4) 46 (2013), 405–448.Google Scholar
Calmès, B., Zainoulline, K. and Zhong, C., A coproduct structure on the formal affine Demazure algebra, Math. Z. 282 (2016), 1191–1218.Google Scholar
Calmès, B., Zainoulline, K. and Zhong, C., Push-pull operators on the formal affine Demazure algebra and its dual, Manuscripta Math. (2018),https://doi.org/10.1007/s00229-018-1058-4.Google Scholar
Calmès, B., Zainoulline, K. and Zhong, C., Equivariant oriented cohomology of flag varieties, Documenta Math., Extra Volume: Alexander S. Merkurjev’s Sixtieth Birthday (2015), 113–144.Google Scholar
Carrell, J., The Bruhat graph of a Coxeter group, a conjecture of Deodhar, and rational smoothness of Schubert varieties, in Algebraic groups and their generalizations: classical methods (University Park, PA, 1991), Proc. Sympos. Pure Math., 56, Part 1, pp. 53–61 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Carrell, J. and Kuttler, J., Smooth points of T-stable varieties in G/B and the Peterson map, Invent. Math. 151 (2003), 353–379.Google Scholar
Demazure, M., Invariants symétriques entiers des groupes de Weyl et torsion, Invent. Math. 21 (1973), 287–301.Google Scholar
Demazure, M., Désingularisation des variétés de Schubert généralisées, Ann. Sci. Éc. Norm. Supér (4) 7 (1974), 53–88.Google Scholar
Deodhar, V., On some geometric aspects of Bruhat orderings II. The parabolic analogue of Kazhdan–Lusztig polynomials, J. Algebra 111 (1987), 483–506.Google Scholar
Edidin, D. and Graham, W., Equivariant intersection theory, Invent. Math. 131 (1998), 595–634.Google Scholar
Fulton, W., Young Tableaux, London Math. Soc. Student Texts, Volume 35 (Cambridge University Press, Cambridge and New York, 1997).Google Scholar
Graham, W., Equivariant $K$-theory and Schubert varieties, Preprint, 2002.Google Scholar
Heller, J. and Malagon-Lopez, J., Equivariant algebraic cobordism, J. Reine Angew. Math. 684 (2013), 87–112.Google Scholar
Hoffnung, A., Malagón-López, J., Savage, A. and Zainoulline, K., Formal Hecke algebras and algebraic oriented cohomology theories, Selecta Math. (N.S.) 20 (2014), 1213–1245.Google Scholar
Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras, Invent. Math. 53 (1979), 165–184.Google Scholar
Knutson, A., A Schubert calculus recurrence from the noncomplex $W$-action on $G/B$,arXiv:math.CO/0306304.Google Scholar
Kostant, B. and Kumar, S., T-Equivariant K-theory of generalized flag varieties, J. Differential Geom. 32 (1990), 549–603.Google Scholar
Kostant, B. and Kumar, S., The nil Hecke ring and cohomology of G/P for a Kac-Moody group G, Adv. Math. 62 (1986), 187–237.Google Scholar
Krichever, I., Formal groups and the Atiyah-Hirzebruch formula, Izv. Akad. Nauk SSSR Ser. Math. 38 (1974), 1289–1304. English transl. in Math. USSR Izv. 8 (1974), 1271–1285.Google Scholar
Leclerc, M.-A., The hyperbolic formal affine Demazure algebra, Algebr. Represent. Theory 19 (2016), 1043–1057.Google Scholar
Lenart, C. and Zainoulline, K., Towards generalized cohomology Schubert calculus via formal root polynomials, Math. Res. Lett. 24 (2017), 839–877.Google Scholar
Lenart, C. and Zainoulline, K., A Schubert basis in equivariant elliptic cohomology, New York J. Math. 23 (2017), 711–737.Google Scholar
Levine, M. and Morel, F., Algebraic Cobordism, Springer Monographs in Math., xii+244pp (Springer, Berlin, 2007).Google Scholar
Maulik, D. and Okounkov, A., Quantum groups and quantum cohomology,arXiv:1211.1287.Google Scholar
Peterson, D., Lecture Notes on Schubert Calculus (MIT, Spring, 1997).Google Scholar
Silverman, J. H., The Arithmetic of Elliptic Curves, Second edition, Graduate Texts in Mathematics 106, xx+513 pp (Springer, Dordrecht, 2009).Google Scholar
Soergel, W., Kazhdan–Lusztig polynomials and a combinatorics for tilting modules, Represent. Theory 1 (1997), 83–114.Google Scholar
Schémas en groupes, III: Structure des schémas en groupes réductifs. (French) Séminaire de Géométrie Algébrique du Bois Marie 1962/64 (SGA 3). Dirigé par M. Demazure et A. Grothendieck. Lecture Notes in Mathematics, Volume 153 (Springer, Berlin-New York, 1970) viii+529.Google Scholar
Stembridge, J., On the fully commutative elements of Coxeter groups, J. Algebraic Combin. 5 (1996), 353–385.Google Scholar
Su, C., Zhao, G. and Zhong, C., On the K-theory stable bases of the Springer resolution, Ann. Sci. Éc. Norm. Supér. to appear. arXiv:1708.08013.Google Scholar
Totaro, B., Chern numbers for singular varieties and elliptic homology, Ann. of Math. (2) 151(2) (2000), 757–791.Google Scholar
Totaro, B., The Chow ring of a classifying space, in Algebraic K-theory (Seattle, WA, 1997), Proc. Sympos. Pure Math., 67, pp. 249–281 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Tymoczko, J., Permutation representations on Schubert varieties, Amer. J. Math. 130 (2008), 1171–1194.Google Scholar
Tymoczko, J., Divided difference operators for partial flag varieties, arXiv:0912.2545.Google Scholar
Zhao, G. and Zhong, C., Elliptic affine Hecke algebras and their representations, arXiv:1507.01245.Google Scholar