1. Introduction
In recent years remarkable progress in the fabrication of bright UV and blue-green light emitting diodes and laser diodes has been achieved for III-N epilayers grown mainly on (0001) sapphire substrates [1]. The peculiarities specific to the growth of GaN films on lattice-mismatched sapphire substrates cause remarkable macro- and micro deformations in the epilayers for different thermal expansion coefficients of the film and the substrate. X-ray diffraction is used to study the material structural properties as well as macro- and micro-strains in GaN and related compounds. Defects in epitaxial layers are usually inspected using measurement of the angular full width at half maximum (FWHM) of the X-ray diffraction rocking curves. However, it is insufficient to establish a type of defect and to clarify the mechanism of stress relaxation and its influence on the optical and electrical properties of the epilayers. In this paper both undoped and Si-doped GaN epilayers have been studied comprehensively by means of double- and triple-crystal diffractometry.
2. Experiment
The GaN single epilayers with specular surfaces, both undoped and doped with Si, were grown in a conventional MOCVD system at a low pressure, 200 mbar. Ammonia and trimethylgallium were applied as component precursors. Purified hydrogen was used as a carrier gas. Silane was used for doping. The substrates were (0001) optical-grade polished sapphire. The growth procedure included GaN nucleation layer deposition at a low temperature of 500 °C followed by epilayer growth at a higher temperature of 1040 °C The typical layer thickness was 2-4 μm. The two-dimensional growth mode appeared to be dominant on the specular surfaces. Hexagonal growth features were lacking, whereas growth steps of ~0.3 nm height were well defined by AFM.
The angular distribution of the X-ray diffraction corresponding to the (0002), (0004), (10

Figure 1. X-ray measurement of epitaxial GaN layers on double-crystal (DCD)- and triple-crystal (TCD)- diffractometer
Schema for the diffracted beam intensity distribution in the scattering plane for symmetrical and asymmetrical Bragg- and Laue-geometry are given in Figure 2 and Figure 3. The measured values of FWHM are designated as ωη B, ωη L and ωα B, ωα L for θ- and θ-2θ scanning mode, in Bragg- and Laue-geometry respectively. In nonplanar geometry ωnc was measured.

Figure 2. Distribution of intensity around (1124) reflection in asymmetric Bragg geometry for γ0<γh and γ0>γh, k0 and kh - vectors of incident and diffracted X-ray waves, ωη- double-crystal FWHM for θ - scanning mode.

Figure 3. Distribution of intensity around (1124) reflection in asymmetric Bragg geometry for γ0<γh and γ0>γh, k0 and kh - vectors of incident and diffracted X-ray waves, ωη- double-crystal FWHM for θ - scanning mode.
On the basis of these parameters, five independent components of the microdistortion tensor ϵzz, ϵzx, ϵxx,ϵxz, and ϵxy were evaluated and the average sizes of grains (average size of the coherent scattering areas ) both in the layer plane τx, and along the c-axis τz, were determined. This approach is discussed in detail in another paper. Reference Kyutt, Leszczynski and Argunova[2] These components of the tensor are related to the type, position, and density of dislocations. The microdistortion tensor components and the average size of the coherent scattering areas (domain size), τx and τz, are given in the Table 1 for undoped and Si-doped GaN epilayers. It should be noted that the Si concentration in the undoped GaN layer was taken to be 5·1016 cm−3, corresponding to the sensitivity limit of SIMS.
Table 1 Two-tailed Spearman's rank correlations between the last Cornell score before death and neuropathological Alzheimer disease scores

The values of the sample curvature radii R and lattice parameters a and c were utilized to evaluate the biaxial stress, σa, and the macrodeformations, ϵa and ϵc, using the expressions:

where s and l denote the substrate and layer, respectively. The accuracy of the values of compressive stress, dislocation density and domain size determined from the measurements did not exceed 30%. The parameters a0 and c0 were taken from reference Reference Porowski, Suski, Perlin, Teisseyre, Grzegory, Bockowski, Yun, Kyutt and Major[3].
The concentration of Si atoms was determined by secondary-ion mass spectrometry (SIMS). The electrical characteristics of the layers were determined using Hall- effect measurements.
3. Results
The relationship between biaxial strain and hydrostatic strain in the grown epilayers is given in Figure 4. It should be noticed that both undoped and Si-doped GaN epilayers were compressed (σa < 0), but the stress was higher in the undoped epilayer. Moreover, the undoped GaN films tolerated practically pure biaxial strain, whereas heavily Si-doped GaN films (n> 2×1019cm−3) tolerated hydrostatic strain mainly. In the epilayers with moderate Si-doping there was coexistence of biaxial and hydrostatic strain fields. Biaxial strain was reduced as Si-doping increased. Comparison of the measured dependence of ϵa/ϵc on the biaxial stress σa with the calculated dependence suggested a type of native defect, such as interstitial Si in the GaN lattice, in these epilayers. The results of SIMS and Hall- effect measurements correlated with this suggestion (see Figure 5).

Figure 4. Dependence of ϵc/ϵa on biaxial stress σa. + – experiment, solid line – calculated. Calculations were performed based on equation from ref. Reference Krüger, Ruvimov, Suski, Ager, Jones, Lilienthal-Weber, Rubin, Bremser and Davis[5]. For pure biaxial strain ϵc/ϵa=-2ν/(1-ν). For combination of biaxial and hydrostatic strain ϵa=(1-bC)(1+(1-ν)σα/E)-1, ϵc=(1-bC)(1-2νσα/E)-1, where ν - Poisson ratio, E - Young modulus, C- impurity concentration, b - contraction coefficient.

Figure 5. The density of vertical edge (1), screw (2) dislocations and misfit dislocations (3) parallel to the interface in relation to Si doping
The application of differential diffractometry allowed a set of structural peculiarities to be revealed in the GaN epilayers.
Specific features of X-ray diffraction in GaN are as follows
-
a) ωη >> ωα, both for Bragg- and for Laue geometry;
-
b) ωη 0002≅ωα 0004, i.e. the influence of the size effect on the value of FWHM is minimal;
-
c) ωη 1124 (γ0 < γh) < ωη 0002, i.e. the contribution of grain misorientation to the value of FWHM is minimal.
Thus, the diffraction spot was elongated along the layer surface. This anisotropy was caused both by anisotropy of the defect dilatation field (ϵzx > ϵxz, ϵxx > ϵzz ) and by anisotropy of the grain size (see Table 1). A similar distribution of the diffracted intensity was observed earlier for epitaxial systems with large lattice-mismatch. Reference Sorokin, Argunova, Kisielowski and Ruvimov[4]
An analysis of the defect structure was performed using the relationship between components of the microdistortion tensor, the types of dislocations and their spacing in the GaN layer. For example, vertical screw dislocations with Burgers vector b parallel to the surface normal n(b || n) made a major contribution to the component ϵzx . Vertical edge dislocations (b ⊥ n) and horizontal edge dislocations (b ⊥ n) ( so-called misfit dislocations), made a contribution to the component ϵxx . Misfit dislocations also made a major contribution to the component ϵxz. In addition, vertical edge dislocations (b ⊥ n)made a major contribution to the component ϵxx .
The density of dislocations ρ is connected to the components of the microdistortion tensor via the expression:
To compare the behavior of similar types of dislocations, the dislocation density was normalized to that of the undoped layer. The dislocation density was found to increase nonlinearly in the range of Si concentration from 1018 to 8×1019cm−3. The dependence of the normalized density on Si concentration is presented in Figure 6 for different types of dislocations. It should be noticed that the dependence is minimized at the smallest ratio of Si concentration to electron concentration. It corresponds to a Si concentration of 8×1018cm−3.

Figure 6. The density of vertical edge (1), screw (2) dislocations and misfit dislocations (3) parallel to the interface in relation to Si doping
The density of misfit dislocations parallel to the interface was always 9-25 times (sometimes up to two orders of magnitude) larger for the Si doped layers than for the undoped layers (Figure 6, curve 3). The density of micropipes also varied nonlinearly with the Si concentration. Micropipes were scarcely observed at a Si concentration of 8×1018− 2×1019cm−3, whereas their density abruptly increased to 109cm−2 at a Si concentration of 5-8 x1019cm−3. For the undoped epilayers, the density was less than 105cm−2.
The doping concentration dependence of the compression stress was also nonlinear and passed a minimum at a Si concentration of 8×1018cm−3 (Figure 6), again at the smallest ratio of Si concentration to electron concentration. It means that the highest portion of the electrically active Si is in the layer. Moreover, it was found that the introduction of Si reduced the size of the coherent scattering areas. The dependence of the domain size on the Si concentration is presented in Figure 7. It should be noted that the dependence is also nonlinear.

Figure 7. Variation of the domain size of columnar structure with Si doping
The maximum mobility in Figure 5 was obtained for the layers with the minimum compressive stress, with the minimum size of the domains along the c axis, and at a higher density of both misfit dislocations parallel to the interface and other type of dislocations, compared to the undoped layers. The density of vertical screw and edge dislocations was also minimal, while micropipes were almost absent.
A decrease in both the size of the domains in the columnar structure along the c axis and of misfit dislocations parallel to the interface seems to be favorable for forming channels for carrier transport which promoted an increase in mobility in the Si-doped epilayers. The results suggest that the controlling structural factors influencing carrier transport are the size of the domains along the c axis and the density of misfit dislocations parallel to the interface.
4. Conclusion
The investigations showed that Si doping significantly changed relaxation of stress in the structure of GaN epilayer-Al2O3. Si doping reduced biaxial stress in the layer, and varied the size of the domains in the columnar structure along the c axis, the density of micropipes, the density of vertical screw and edge dislocations, and the density of misfit dislocations parallel to the interface.
Both undoped and Si-doped GaN epilayers were compressed, but the stress was higher in the undoped epilayer. Moreover, the undoped GaN films tolerated practically pure biaxial strain, whereas heavily Si-doped GaN films (n> 2×1019cm−3) tolerated mainly hydrostatic strain. In the epilayers with moderate Si-doping there was coexistence of biaxial and hydrostatic strain fields. Biaxial stress reduced as Si-doping increased. At the same time an increase in electron mobility from 20 to 200-260 cm2 V−1 s−1 was observed
A comparison of the measured dependence of ϵa/ϵc on the biaxial stress σa with the calculated dependence suggested a type of the native defect, such as interstitial Si, in these epilayers.
Si doping resulted in increasing both diagonal components ϵzz, ϵxx and off-diagonal components ϵzx,ϵxz, and ϵxy of the microdistortion tensor. At the same time, the average size of the coherent scattering areas (domain size) τx and τz decreased.
A decrease in the size of the domains in the columnar structure along the c axis and of misfit dislocations parallel to the interface seems to be favorable for forming channels for carrier transport.

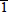 0), (20
0), (20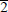 0), and (11
0), and (11







