Hostname: page-component-77c89778f8-rkxrd Total loading time: 0 Render date: 2024-07-17T04:28:06.026Z Has data issue: false hasContentIssue false
  • English
  • Français

A footnote to the theory of double integrals

Published online by Cambridge University Press:  23 January 2015

Juan Pla
Juan Pla*
Affiliation:
315 rue de Belleville, 75019 Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

The probability integral theorem, which states that

is on the record for having enticed numerous mathematicians to find alternative proofs for it, over a period of more than two centuries, till recent times (for a few recent references see [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]). The most popular demonstration (attributed to the French mathematician Poisson; see [11], in references of [12]), the one found in almost all textbooks, relies on the double integral

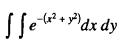
(taken over the upper-right quarter of the Cartesian plane) obtained by squaring the probability integral. By resorting to polar coordinates and writing down the above integral as:

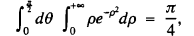
the value of the probability integral is obtained by taking the square root of the result on the right-hand side of this latter relation.

Type
Articles
Information
The Mathematical Gazette , Volume 94 , Issue 530 , July 2010 , pp. 262 - 269
Copyright
Copyright © The Mathematical Association 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Nicholas, C. P. and Yates, R. C., The probability integral, Amer. Math. Month. 57 (1950) pp. 412–413.CrossRefGoogle Scholar
2. Nicholas, C. P., Another look at the probability integral, Amer. Math. Month. 64 (1957) pp. 739–741.Google Scholar
3. Gauthier, N., Evaluating the probability integral, Math. Gaz. 72 (June 1988) pp. 124–125.Google Scholar
4. Desbrow, Darrell, Evaluating the probability integral, Math. Gaz. 74 (June 1990) pp. 169–170.CrossRefGoogle Scholar
5. Weinstock, Robert, Elementary evaluations of and , Amer. Math. Month. 97 (1990) pp. 39–42.Google Scholar
6. Lord, Nick, An elementary single-variable proof of , Math. Gaz. 87 (July 2003) pp. 308–311.Google Scholar
7. Young, Robert M., On evaluating the probability integral: a simple one-variable proof, Math. Gaz. 89 (July 2005) pp. 252–254.CrossRefGoogle Scholar
8. Jameson, T. P., The probability integral by volume of revolution, Math. Gaz. 78 (November 1994) pp. 339–340.CrossRefGoogle Scholar
9. Loya, Paul, Dirichlet and Fresnel integrals via iterated integration, Math. Mag. 78 (February 2005) pp 63–67.Google Scholar
10. Boros, George and Moll, Victor, Irresistible integrals, Cambridge University Press (2004) pp. 164–169.Google Scholar
11. Sturm, J. C. F., Cours d'analyse de l'Ecole Poly technique, vol 2, Mallet-Bachelier, Paris (1859) pp. 16–18.Google Scholar
12. Dawson, Robert J. MacG, On a ‘singular’ integration technique of Poisson, Amer. Math. Month. 112 (2005) pp. 270–272.Google Scholar
13. Pendelbury, R., On the squares of trancendents, Mess. Math. 1 (1872) pp.131–135.Google Scholar
14. Gradshteyn, I. S. and Ryzbyk, I. M. Table of integrals, Series and Products (6th edn.), Academic Press (2000).Google Scholar