No CrossRef data available.
Article contents
A Descriptive Proof of a Theorem for Conic Sections
Published online by Cambridge University Press: 03 November 2016
Extract
1 To prove that a line meeting one given conic in points harmonic to its intersections with another given conic, touches a conic.
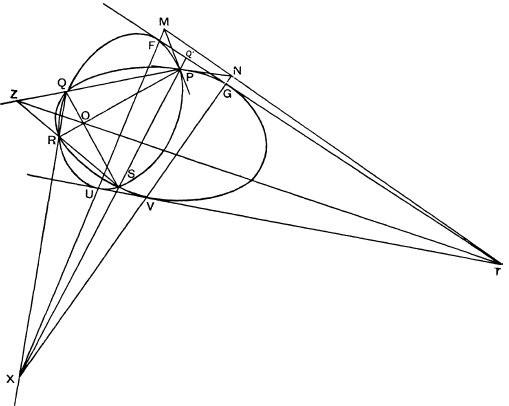
2. Lemma I. Let two conies intersect in P, Q, R, S as shown in Fig. 1.
Let UV, FG be a pair of common tangents intersecting in T, and let the tangents at P to the two conies cut UF, VG in the points M, N respectively. Then M, N, T are collinear
For: QR, PS, FU, GV all meet in a point X, and the range MFUX is related to the pencil P(PFUS), which is related to F(PFUS), which is related to PQ′XS, where Q′ is the intersection of SP and FG Similarly, NGVX is related to PQ′XS. Hence MFUX and NGVX are related, and thus MN passes through T
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association
References
page no 165 note * See Baker, , Principles of Geometry, ii. 61, par. 2 Google Scholar.
page no 165 note † Baker, ii. 37.
page no 166 note * Baker, ii. 37.


