Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T14:27:15.107Z Has data issue: false hasContentIssue false
  • English
  • Français

A kaleidoscope of solutions for a Diophantine system

Published online by Cambridge University Press:  23 January 2015

Juan Pla
Juan Pla*
Affiliation:
315 rue de Belleville, 75019 Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

A classical exercise in recreational mathematics is to find Pythagorean triples such that the legs are consecutive integers. It is equivalent to solve the Pell equation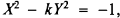 with k = 2. In this case it provides all the solutions (see [1] for details). But to obtain all the solutions of a Diophantine system in one stroke is rather exceptional. Actually this note will show that the analogous problem of finding four integers A, B, C and D such that

Type
Articles
Information
The Mathematical Gazette , Volume 94 , Issue 529 , March 2010 , pp. 42 - 50
Copyright
Copyright © The Mathematical Association 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Beiler, Albert H., Recreations in the theory of numbers, Dover (1966) pp. 122–125.Google Scholar
2. Sierpinski, W., Elementary theory of numbers, North Holland (1988) pp.66–69.Google Scholar
3. Carmichael, R. D., Diophantine analysis, Dover (1959) pp. 38–43.Google Scholar
4. Spira, Robert, The Diophantine equation , Amer. Math. Monthly 69 (1962) pp. 360–365.Google Scholar
5. Dickson, Leonard E., History of the theory of numbers, Carnegie Institution of Washington, Washington (1920) vol 2.Google Scholar
6. Cossali, Pietro, Storia critica dell'origine, transporto in Italia e primi progressi in essa dell' Algebra, Parma (1797), p. 97 (as quoted by Dickson, L. E.).Google Scholar
7. Problem 605: Nearly isosceles Pythagorean quadruples, Coll. Math. Journal 29 (May 1998) pp. 247–248.Google Scholar
8. Hirschhorn, Mike, Feedback on 90.06, Math. Gaz. 91 (March 2007) p.153.Google Scholar
9. Weil, André, Number theory: an approach through history, Birkhäuser (1983).Google Scholar