Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-30T08:05:55.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical integration — a different approach

Published online by Cambridge University Press:  01 August 2016

Harry V. Smith
Harry V. Smith*
Affiliation:
22 Hodgson Avenue, Leeds LS17 8PQ email: hvs2@tutor.open.ac.uk
Get access Rights & Permissions [Opens in a new window]

Extract

In common with, I suspect, many people the author does not have access to the NAG library and so, when I was asked recently to calculate the value of the integral

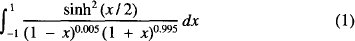
correct to 10 decimal places my first reaction was to try several different calculators as well as several mathematical software packages. On doing so it was disappointing to find they either gave widely differing values such as 7.9065200767, 4.1317217452 or 0.9174196842 or an error message indicating that the method had not converged.

Type
Articles
Information
The Mathematical Gazette , Volume 90 , Issue 517 , March 2006 , pp. 21 - 24
Copyright
Copyright © The Mathematical Association 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. The NAG Fortran Library, Numerical Algorithms Group Ltd., 256 Banbury Road, Oxford OX2 7DE.Google Scholar
2. Ralston, A., A first course in numerical analysis, McGraw-Hill (1965).Google Scholar
3. Evans, G. A., Practical numerical integration, Wiley (1993).Google Scholar
4. Bell, W. W., Special functions for scientists and engineers, Van Nostrand (1968).Google Scholar
5. Stenger, F., Bounds on the error of Gauss-type quadratures, Numer. Math. 8 (1966) pp. 150–160.Google Scholar
6. Smith, H. V. and Hunter, , The numerical evaluation of a class of divergent integrals, International Series of Numerical Mathematics 85 (1988) pp. 274–284.CrossRefGoogle Scholar
7. Abramowitz, M. and Stegun, I. A. (eds), Handbook of mathematical functions, Dover (1966).CrossRefGoogle Scholar