Hostname: page-component-84b7d79bbc-7nlkj Total loading time: 0 Render date: 2024-07-25T14:50:06.740Z Has data issue: false hasContentIssue false
  • English
  • Français

The regularity of randomness†

Published online by Cambridge University Press:  22 September 2016

S. J. Taylor
S. J. Taylor*
Affiliation:
Department of Pure Mathematics, The University, Liverpool L69 3BX
Get access Rights & Permissions [Opens in a new window]

Extract

My title seems self contradictory, for surely random happenings are essentially unpredictable—so how can they be regular? And yet this apparent contradiction is the key which justifies the mathematical model of probability theory. For the regularity is the basic reason for our model providing a new mathematical tool with powerful applications to analysis, potential theory, number theory, quantum theory, statistical mechanics....

Let us start by asking, “What is probability?” What do I mean if I say “When you toss a coin there is a probability ½ that it turns up a head” or “When you pick a card from a well shuffled pack there is probability 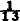that it will be an ace”?

Type
Research Article
Information
The Mathematical Gazette , Volume 62 , Issue 419 , March 1978 , pp. 1 - 8
Copyright
Copyright © Mathematical Association 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

A slightly amended version of a lecture delivered to the Mathematical Association Annual Conference in Liverpool, April 1977.

References

1. Taylor, S. J., Exploring mathematical thought. Ginn (1970).Google Scholar
2. Feller, W., An introduction to probability theory and its applications. Vol. 1 (3rd edition). Wiley (1968).Google Scholar
3. Erdös, P., On the law of iterated logarithm, Ann. Math. 43,419–436 (1942).CrossRefGoogle Scholar
4. Ito, K. and McKean, H. P., Diffuston processes and their sample paths. Springer (1965).Google Scholar
5. Taylor, S. J., Sample path properties of processes with stationary independent increments, in Stochastic analysis, edited by Kendall, D. G. and Harding, E. F.. Wiley (1973).Google Scholar
6. Doob, J. L., Interrelations between Brownian motion and potential theory, Proc. Int. Congr. Math. (Vol. 3), 202–204 (1954).Google Scholar
7. Burgess, Davis, Picard’s theorem and Brownian motion, Trans. Am. math. Soc. 213, 353–362 (1975).Google Scholar