Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-07-05T20:19:57.339Z Has data issue: false hasContentIssue false
  • English
  • Français

Envelopes and characteristics

Published online by Cambridge University Press:  24 October 2008

J. W. Bruce
J. W. Bruce
Affiliation:
Department of Pure Mathematics, University of Newcastle upon Tyne
Get access Rights & Permissions [Opens in a new window]

Extract

Envelopes of hypersurfaces arise in many different geometric situations. For example, the canal surfaces associated with a space curve can be obtained as the envelope of spheres of a fixed radius centred on that curve. (Other examples can be found in [11], chapter II and [4], chapter 5). In what follows we shall be entirely concerned with the local structure of such envelopes. So essentially we have a smooth map germ 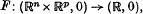with 0 a regular value of the restriction of F to 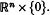. For 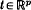near 0 we have 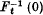a smooth hypersurface near 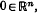, where 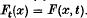. The envelope of this family of hypersurfaces is obtained by eliminating t from the equations 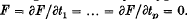. Moreover, it can be identified with the discriminant of F viewed as an unfolding, by the x variables, of the function germ 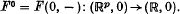. This observation, together with standard results on versal unfoldings of functions, allows one to determine the local structure of many ‘generic’ geometric envelopes. See [2] for details.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 100 , Issue 3 , November 1986 , pp. 475 - 492
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arnold, V. I.. Wavefront evolution and equivariant Morse lemma. Comm. Pure Appl. Maths. 29 (1976), 557–582.CrossRefGoogle Scholar
[2]Bruce, J. W.. On singularities, envelopes and elementary differential geometry. Math. Proc. Cambridge Philos. Soc. 89 (1981), 43–48.CrossRefGoogle Scholar
[3]Bruce, J. W.. Functions on discriminants. J. London Math. Soc. 30 (1985), 551–567.Google Scholar
[4]Bruce, J. W. & Giblin, P. J.. Curves and Singularities (Cambridge University Press, 1984).Google Scholar
[5]Martinet, J.. Déploiments versels des applications différentiables et classification des applications stables. In Singularités d'applications différentiables. Lecture Notes in Mathematics, vol. 535 (Springer-Verlag, 1976).CrossRefGoogle Scholar
[6]Martinet, J.. Singularities of Smooth Functions and Maps. LMS Lecture Notes Series, 58 (Cambridge University Press, 1982).Google Scholar
[7]Saito, K.. Theory of logarithmic differential forms and logarithmic vector fields. J. Fac. Sci. Univ. Tokyo Sec. I A, 27 (1980), 265–792.Google Scholar
[8]Saito, K.. Primitive forms for an unfolding of a function with an isolated critical point. J. Fac. Sci. Univ. Tokyo Sec. 1A Math, 28 (1982), 775–792.Google Scholar
[9]Teissier, B.. The hunting of invariants in the geometry of discriminants. Proc. Nordic Summer School/NAVF Symposium in Math. (ed. Holm, Per). Sijthoff and Noordhoff, 1977, 565–677.Google Scholar
[10]Terao, H.. Discriminant of a holomorphic map and logarithmic vector fields. J. Fac. Sci. Univ. Tokyo Sec. 1A, 30 (1983), 379–391.Google Scholar
[11]Weatherburn, C. E.. Differential geometry of three dimensions, vol. 1 (University Press, Cambridge, 1931).Google Scholar
[12]Zakalyukin, V. M.. Bifurcations of wavefronts depending on one parameter. Fund. Anal. Appl. 10 (1976), 139–140.CrossRefGoogle Scholar