Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T14:23:06.914Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of outgoing solutions for perturbations of and applications to the scattering matrix

Published online by Cambridge University Press:  24 October 2008

Kazuhiro Yamamoto
Kazuhiro Yamamoto
Affiliation:
Department of Mathematics, Nagoya Institute of Technology, Nagoya, Gokiso-cho, 466, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we shall prove an existence theorem and give applications of an outgoing solution of the following problem:

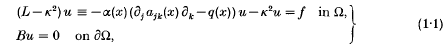
where L(x, x) is a second order elliptic differential operator with a potential term q(x), is an exterior domain of ℝn (where n 2) with the C2-class boundary , k is an element of the complex plane or of a logarithmic Riemann surface, and B is either a Dirichlet boundary condition or of the form Bu = vj(x) ajk(x) ku + (x)u with the unit outer normal vector v(x) = (vl,, vn) at x.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 2 , March 1992 , pp. 399 - 415
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Agmon, S.. Spectral properties of Schrdinger operators and scattering theory. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 2 (1975), 151218.Google Scholar
2Alsholm, P. and Schmidt, G.. Spectral and Scattering Theory for Schrdinger Operators (Mathematisk Institut, Aarhus University, 1969).Google Scholar
3Babbitt, D. and Balslev, E.. Local distortion techniques for and unitarity of the S-matrix for the 2-body problem. J. Math. Anal. Appl. 54 (1974), 316347.CrossRefGoogle Scholar
4Balslev, E.. Analyticity properties of eigenfunctions and scattering matrix. Comm. Math. Phys. 114 (1988), 599612.CrossRefGoogle Scholar
5Dolph, C. L., McLeod, J. B. and Thoe, D.. The analytic continuation of the resolvent kernel and scattering operator associated with the Schrdinger operator. J. Math. Anal. Appl. 16 (1966), 311332.CrossRefGoogle Scholar
6Ikebe, T.. Spectral representation for Schrdinger operators with long range potentials II, Perturbation by short-range. Publ. Res. Inst. Math. Sci. 11 (1976), 551558.CrossRefGoogle Scholar
7Jensen, A.. Resonances in an abstract scattering theory. Ann. Inst. H. Poincar Sect. A. 33 (1980), 209223.Google Scholar
8Landis, E. M.. On some properties of solutions of elliptic equations. Dokl. Akad. Nauk SSSR 107 (1956), 640643.Google Scholar
9Lax, P. D. and Phillips, R. S.. Scattering Theory (Academic Press, 1967).Google Scholar
10Lax, P. D. and Phillips, R. S.. Scattering theory for the acoustic equations in an even number of space dimensions. Indiana Univ. Math. J. 22 (1972), 101134.CrossRefGoogle Scholar
11Lax, P. D. and Phillips, R. S.. The acoustic equation with an indefinite energy form and the Schrdinger equation. J. Funct. Anal. 1 (1967), 3783.CrossRefGoogle Scholar
12Majda, A.. Outgoing solutions for perturbations of with applications to spectral and scattering theory. J. Differential Equations 16 (1974), 515547.CrossRefGoogle Scholar
13Mochizuki, K.. Growth properties of solutions of second order elliptic differential equations. J. Math. Kyoto Univ. 16 (1976), 351373.Google Scholar
14Mochizuki, K.. Spectral and scattering theory for second order elliptic operators in an exterior domain. Lecture notes, University of Utah, (1972).Google Scholar
15Mochizuki, K.. Scattering theory for the wave equation. Kinokuniya Schoten, Tokyo, 1984 (in Japanese).Google Scholar
16Phillips, R. S.. Scattering theory for the wave equation with a short range perturbation. Indiana Univ. Math. J. 31 (1982), 609639.CrossRefGoogle Scholar
17Protter, M. H.. Unique continuation for elliptic equations. Trans. Amer. Math. Soc. 95 (1960), 8191.CrossRefGoogle Scholar
18Reed, M. and Simon, B.. Methods of Modern Mathematical Physics, vol. 3 (Academic Press, 1979).Google Scholar
19Saito, Y.. Extended limiting absorption method and analyticity of the S-matrix. J. Heine Angew. Math. 343 (1983), 122.Google Scholar
20Seeley, R. T.. Integral equations depending analytically on a parameter. Indag. Math. 24 (1962), 434442,CrossRefGoogle Scholar
21Seeley, R. T.. Integral equations depending analytically on a parameter. Indag. Math., 25 (1963), 654.CrossRefGoogle Scholar
22Shenk, N. A.. Eigen function expansions and scattering theory for the wave equation in an exterior region. Arch. Rational Mech. Anal. 21 (1966), 120150.CrossRefGoogle Scholar
23Shenk, N. and Thoe, D.. Outgoing solutions of ( + q k 2)u = f in an exterior domain. J. Math. Anal. Appl. 31 (1970), 81116.CrossRefGoogle Scholar
24Shenk, N. and Thoe, D.. Eigenfunction expansions and scattering theory for perturbations of . J. Math. Anal. Appl. 36 (1971), 313351.CrossRefGoogle Scholar
25Thoe, D.. Spectral theory for the wave equation with a potential term. Arch. Rational Mech. Anal. 22 (1966), 364406.CrossRefGoogle Scholar
26Vainberg, B. R.. On the short wave asymptotic behavior of solutions of stationary problems and the asymptotic behavior as t of solutions of non-stationary problems. Russian Math. Surveys. 30 (1975), 158.CrossRefGoogle Scholar
27Watson, G. N.. A Treatise on the theory of Bessel Functions, 2nd edition (Cambridge University Press, 1962).Google Scholar
28Weder, R.. Analyticity of the scattering matrix for wave propagation in crystals. J. Math. Pures Appl. 64 (1985), 121148.Google Scholar
29Yamamoto, K.. Scattering theory and spectral representations for general wave equations with short range perturbations. Canad. J. Math. 43 (1991), to appear.CrossRefGoogle Scholar
30Yamamoto, K.. The behavior of the analytically continued resolvent operator near k = 0 and an application to the energy decay. Proc. Amer. Math. Soc., to appear.Google Scholar