Hostname: page-component-77c89778f8-cnmwb Total loading time: 0 Render date: 2024-07-18T04:30:11.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of solutions of Hammerstein equations of compact type

Published online by Cambridge University Press:  24 October 2008

Ronald I. Becker
Ronald I. Becker
Affiliation:
University of Cape Town
Get access Rights & Permissions [Opens in a new window]

Abstract

The existence of solutions is considered for equations of the form

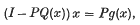
for x ∈ H (a Hilbert space), P a compact linear operator on H; Q(x) a bounded linear operator on H and continuous in x and uniformly bounded; g(x) a continuous uniformly bounded map with range in H. Two situations are considered: Q(x) lies in a weakly compact set of operators for which (a) (I − PQ(x)) is invertible (non-resonance case) or (b) (I − P(Q(x) + λI)) is invertible for 0 < λ ≤ α (resonance case).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 1 , January 1981 , pp. 149 - 158
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Becker, R. I.Periodic solutions of semilinear equations of evolution of compact type. To appear J. Math. Anal. Appl.Google Scholar
(2)Cesari, L. Functional analysis, nonlinear differential equations and the alternative method. In Non-linear functional analysis and differential equations (Marcel Dekker, New York, 1976), pp. 1–197.Google Scholar
(3)De Figureido, D. G.On the range of nonlinear operators with linear asymptotes which are not invertible. Comment. Math. Univ. Carolinae 15 (1974), 415–428.Google Scholar
(4)Duntord, N. and Schwartz, J. T.Linear operators, vol. I (Interscience, New York, 1958).Google Scholar
(5)Friedman, A.Foundations of modern analysis (Holt, Rinehart and Winston, New York, 1970).Google Scholar
(6)Fučik, S., M. Kučera, M. and Nečas, J.Ranges on nonlinear asymptotically linear operators. J. Diff. Equations 17 (1975), 375–394.CrossRefGoogle Scholar
(7)Kannan, R. and Locker, J.On a class of nonlinear boundary value problems. J. Diff. Equations 26 (1977), 1–8.CrossRefGoogle Scholar
(8)Krasnoselskii, M. A.Topological methods in the theory of non-linear integral equations. (Pergamon Press, Oxford, 1964).Google Scholar
(9)Krein, S. G.Linear differential equations in Banach space (Translations of Mathematical Monographs no. 29, AMS, Providence, 1971).Google Scholar
(10)Landesman, E. A. and Lazer, A. C.Nonlinear perturbations of linear elliptic boundary value problems at resonance. J. Math. Mech. 19 (1970), 609–623.Google Scholar
(11)Lazer, A. C. and Leach, D. E.On a nonlinear two-point boundary value problem. J. Math. Anal. Appl. 26 (1969), 20–27.CrossRefGoogle Scholar
(12)Mawhin, J.An extension of a theorem of A. C. Lazer on forced non-linear oscillations. J. Math. Anal. Appl. 40 (1972), 20–29.CrossRefGoogle Scholar
(13)Laptev, G. I.Eigenvalue problems for second-order differential equations in Banach and Hilbert spaces. Differential'nye uravneniya, (2) 9 (1966), 1151–1160.Google Scholar
(14)Nečas, J.On the range of nonlinear operators with linear asymptotes which are not invertible. Comment. Math. Univ. Carolinae 14 (1973), 63–72.Google Scholar